Với giải Bài 5.33 trang 124 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài tập cuối Chương 5 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài tập cuối Chương 5
Bài 5.33 trang 124 Toán 11 Tập 1: Tìm tập xác định của các hàm số sau và giải thích tại sao các hàm này liên tục trên các khoảng xác định của chúng.
a) ;
b) .
Lời giải:
a) Biểu thức có nghĩa khi x2 + 5x + 6 ≠ 0 ⇔ (x + 2)(x + 3) ≠ 0 
Do đó, tập xác định của hàm số f(x) là ℝ \ {– 3; – 2} = (–∞; – 3) ∪ (– 3; – 2) ∪ (– 2; +∞).
Suy ra hàm số f(x) xác định trên các khoảng (–∞; – 3), (– 3; – 2) và (– 2; +∞). Trên các khoảng này, tử thức (hàm lượng giác) và mẫu thức (hàm đa thức) là các hàm số liên tục. Vậy hàm số liên tục trên các khoảng xác định của chúng.
b) Biểu thức có nghĩa khi sin x ≠ 0 ⇔ x ≠ kπ, k ∈ ℤ.
Do đó, tập xác định của hàm số g(x) là ℝ \ {kπ | k ∈ ℤ}.
Trên các khoảng xác định của hàm số g(x), tử thức x – 2 (hàm đa thức) và mẫu thức sin x (hàm lượng giác) là các hàm số liên tục.
Vậy hàm số liên tục trên các khoảng xác định của chúng.
Video bài giảng Toán 11 Bài tập cuối Chương 5 - Kết nối tri thức
Xem thêm các lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 5.18 trang 123 Toán 11 Tập 1: Cho dãy số (un) với . Mệnh đề đúng là...
Bài 5.19 trang 123 Toán 11 Tập 1: Cho . Giới hạn của dãy số (un) bằng.....
Bài 5.21 trang 123 Toán 11 Tập 1: Cho hàm số . Mệnh đề đúng l....
Bài 5.22 trang 123 Toán 11 Tập 1: Cho hàm số....
Bài 5.23 trang 123 Toán 11 Tập 1: Cho hàm số 
. Hàm số f(x) liên tục trên....
Bài 5.24 trang 123 Toán 11 Tập 1: Cho hàm số Hàm số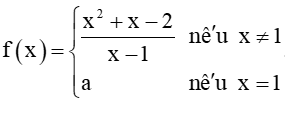 
liên tục tại x = 1 khi.....
Bài 5.26 trang 124 Toán 11 Tập 1: Tìm giới hạn của các dãy số sau:...
Bài 5.28 trang 124 Toán 11 Tập 1: Tính các giới hạn sau:...
Bài 5.29 trang 124 Toán 11 Tập 1: Tính các giới hạn một bên:....
Bài 5.30 trang 124 Toán 11 Tập 1: Chứng minh rằng giới hạn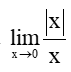 
không tồn tại.....
Bài 5.34 trang 124 Toán 11 Tập 1: Tìm các giá trị của a để hàm số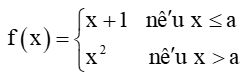
liên tục trên ℝ....
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
. Có kết luận gì về giới hạn của dãy số này?.....
