Với Giải toán 10 trang 73 Tập 2 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải toán 10 trang 73 Tập 2 Chân trời sáng tạo

Bài 1 trang 73 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2).

a) Chứng minh ABCD là một hình vuông.

b) Tìm tọa độ tâm I của hình vuông ABCD.

Lời giải:

Ta có: $\overrightarrow{AB}$ = (-1; 3) ⇒ AB = $\sqrt{{(-1)}^2+3^2}=\sqrt{10}$

$\overrightarrow{DC}$ = (-1; 3) ⇒ DC = $\sqrt{{(-1)}^2+3^2}=\sqrt{10}$

⇒ $\overrightarrow{AB}=\overrightarrow{DC}$ ⇒ AB // CD và AB = DC

⇒ ABCD là hình bình hành (1)

Ta lại có: $\overrightarrow{AD}$ = (3; 1)

⇒ $\overrightarrow{AB}.\overrightarrow{AD}$ = (-1).3 + 3.1 = 0

⇒ $\overrightarrow{AB}\perp \overrightarrow{AD}$

⇒ $\widehat{BAD}=90°$ (2)

Từ (1) và (2) suy ra ABCD là hình vuông.

b) Vì I là tâm của hình vuông ABCD nên I là giao điểm của hai đường cheoc AC và BD hay I là trung điểm của AC. Khi đó tọa độ điểm I là:

 ⇒ I(3; 3).

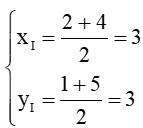
Vậy tọa độ tâm I của hình vuông ABCD là I(3; 3).

Bài 2 trang 73 Toán lớp 10 Tập 2: Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O). Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ để chứng minh EF vuông góc với DB.

Lời giải:

Ta có hình vẽ sau:

Đặt AE = a, EB = b, EC = c, ED = d.

Ta chọn hệ trục tọa độ sao cho E(0; 0), A(a; 0), B(b; 0), C(0; c) và D(0; d) và F(a; c).

Xét ∆AEC và ∆DEB, có:

$\widehat{AEC}=\widehat{DEB}=90°$

$\widehat{CAE}=\widehat{BDE}$ (hai góc nội tiếp cùng chắn $\stackrel{⏜}{CB}$)

⇒ ∆AEC ∽ ∆DEB (g – g)

⇒ $\frac{AE}{DE}=\frac{AC}{DB}=\frac{EC}{EB}$

⇒ $\frac{AE}{DE}=\frac{EC}{EB}$

⇔ AE.EB = DE.EC

⇔ AE.EB = DE.EC

⇔ a.b = d.c

⇔ d.c – ab = 0

Ta có: $\overrightarrow{\text{EF}}$ = (a; c), $\overrightarrow{BD}$ = (-b; d)

⇒ $\overrightarrow{\text{EF}}.\overrightarrow{BD}$ = a.(-b) + c.d = - ab + cd = 0

⇒ $\overrightarrow{\text{EF}}\perp \overrightarrow{BD}$

⇒ EF ⊥ BD.

Bài 3 trang 73 Toán lớp 10 Tập 2: Tìm tọa độ giao điểm và góc giữa hai đường thẳng d₁ và d₂ trong mỗi trường hợp sau:

a) d₁: x – y + 2 = 0 và d₂: x + y + 4 = 0;

b) d₁: 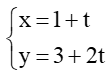 và d₂: x – 3y + 2 = 0;

c) 

Lời giải:

a) Gọi A là giao điểm của đường thẳng d₁ và d₂. Khi đó tọa độ điểm A là nghiệm của hệ phương trình:

⇒ A(-3; -1).

Ta có:

Đường thẳng d₁: x – y + 2 = 0 có VTPT là $\overrightarrow{n_1}$(1; -1);

Đường thẳng d₂: x + y + 4 = 0 có VTPT là $\overrightarrow{n_2}$(1; 1);

Áp dụng công thức tính góc giữa hai đường thẳng ta có:

cos(d₁; d₂) = 

⇒ (d₁; d₂) = 90°

Vậy giao điểm của hai đường thẳng d₁ và d₂ là A(-3; -1) và góc giữa hai đường thẳng d₁ và d₂ là 90°.

b) Ta có: d₁: 

⇔ x – 1 = $\frac{y-3}{2}$

⇔ 2x – 2 = y – 3

⇔ 2x – y + 1 = 0

Gọi B là giao điểm của đường thẳng d₁ và d₂. Khi đó tọa độ điểm B là nghiệm của hệ phương trình:

Ta có:

Đường thẳng d₁: 2x – y + 1 = 0 có VTPT là $\overrightarrow{n_1}$(2; -1);

Đường thẳng d₂: x – 3y + 2 = 0 có VTPT là $\overrightarrow{n_2}$(1; -3);

Áp dụng công thức tính góc giữa hai đường thẳng ta có:

cos(d₁; d₂) = 

⇒ (d₁; d₂) = 45°

Vậy giao điểm của hai đường thẳng d₁ và d₂ là $B\left(-\frac{1}{5};\frac{3}{5}\right)$ và góc giữa hai đường thẳng d₁ và d₂ là 45°.

c) Gọi C là giao điểm của đường thẳng d₁ và d₂. Khi đó tọa độ điểm C là nghiệm của hệ phương trình:

Ta có:

Đường thẳng d₁: 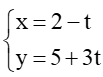 có VTCP là $\overrightarrow{u_1}$ = (-1; 3);

Đường thẳng d₂: 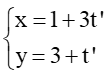 có VTCP là $\overrightarrow{u_2}$ = (3; 1).

Áp dụng công thức tính góc giữa hai đường thẳng ta có:

cos(d₁; d₂) = 

⇒ (d₁; d₂) = 90°

Vậy giao điểm của hai đường thẳng d₁ và d₂ là $C\left(\frac{5}{2};\frac{7}{2}\right)$ và góc giữa hai đường thẳng d₁ và d₂ bằng 90°.

Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Giải toán lớp 10 trang 74 Tập 2

Giải toán lớp 10 trang 75 Tập 2