Với Giải toán 10 trang 35 Tập 2 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải toán 10 trang 35 Tập 2 Chân trời sáng tạo
Thực hành 1 trang 35 Toán lớp 10: Khai triển các biểu thức sau
a)
b)
Phương pháp giải:
Sử dụng công thức nhị thức Newton
Lời giải:
a)
b)
Thực hành 2 trang 35 Toán lớp 10: Sử dụng công thức nhị thức Newton, chứng tỏ rằng
a)
b)
Phương pháp giải:
Sử dụng công thức nhị thức Newton
Lời giải:
a)
(đpcm)
b)
(đpcm)
Vận dụng trang 35 Toán lớp 10: Trên quầy còn 4 vé xổ số khác nhau. Một khách hàng có bao nhiêu lựa chọn mua một số vé trong các số vé đó? Tính cả trường hợp mua không vé, tức là không mua vé nào.
Phương pháp giải:
Sử dụng công thức nhị thức Newton
Lời giải:
Mỗi lựa chọn mua vé của khách hàng đó là một tổ hợp chập k của 4 . Do đó, tổng số lựa chọn mua vé của khách hàng là
Vậy có tất cả 16 lựa chọn mua một số vé trong số các vé xổ số đó.
Bài tập (trang 35)
Bài 1 trang 35 Toán lớp 10: Sử dụng công thức nhị thức Newton, khai triển các biểu thức sau:
a)
b)
Phương pháp giải:
Sử dụng công thức nhị thức Newton
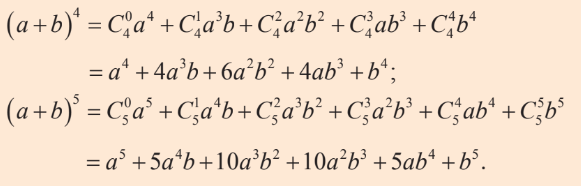
Lời giải:
a)
b)
Bài 2 trang 35 Toán lớp 10: Khai triển và rút gọn các biểu thức sau:
a)
b)
c)
Phương pháp giải:
Sử dụng công thức nhị thức Newton
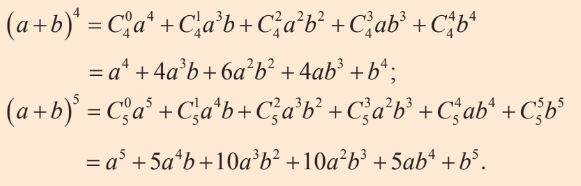
Lời giải:
a) Áp dụng công thức nhị thức Newton, ta có
b) Áp dụng công thức nhị thức Newton, ta có
Từ đó,
c) Áp dụng công thức nhị thức Newton, ta có
Bài 3 trang 35 Toán lớp 10: Tìm hệ số của trong khai triển
Phương pháp giải:
Sử dụng công thức nhị thức Newton
Hệ số của trong khai triển là .
Lời giải:
Áp dụng công thức nhị thức Newton ta có
Hệ số là hệ số của số hạng
Vậy hệ số của là 1080
Bài 4 trang 35 Toán lớp 10: Cho là một tổ hợp có 5 phần tử. Chứng minh rằng tổ hợp con có số lẻ phần tử của A bằng tập hợp con có số chẵn phần tử của A
Phương pháp giải:
Bước 1: Tính các tổ hợp con
Bước 2: Sử dụng công thức nhị thức Newton
Lời giải:
Số tổ hợp con có x phần tử là số tổ hợp chập x của 5.
=> Số tổ hợp con có lẻ phần tử là:
Số tổ con có chẵn phần tử là:
(đpcm)
Bài 5 trang 35 Toán lớp 10: Chứng minh rằng
Phương pháp giải:
Sử dụng công thức nhị thức Newton
Hoặc
Lời giải:
Vậy ta có điều phải chứng minh
Cách 2:
Ta có:
Tương tự:
(đpcm)
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Giải toán lớp 10 trang 33 Tập 2