Với Giải Toán lớp 6 trang 37 Tập 1 Kết nối tri thức chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6. Mời các bạn đón xem:

Giải Toán lớp 6 trang 37 Tập 1 Kết nối tri thức

Bài 2.10 trang 37 Toán lớp 6 Tập 1: Trong các số sau, số nào chia hết cho 2, số nào chia hết cho 5?

324; 248; 2 020; 2025.

Lời giải:

+) Vì các số 324; 248; 2 020 có chữ số tận cùng lần lượt là 4; 8; 0 nên 324; 248; 2 020 chia hết cho 2

+) Vì các số 2 020; 2025 có chữ số tận cùng lần lượt là 0 và 5 nên 2 020; 2025 chia hết cho 5.

Bài 2.11 trang 37 Toán lớp 6 Tập 1: Trong các số sau, số nào chia hết cho 3, số nào chia hết cho 9?

450 ; 123 ; 2 019 ; 2 025.

Lời giải:

+) Xét số 450 có tổng các chữ số 4 + 5 + 0 = 9, vì 9 ⁝ 3 và 9 ⁝ 9 nên 450 ⁝ 3 và 450 ⁝ 9.

+) Xét số 123 có tổng các chữ số 1 + 2 + 3 = 6, vì 6 ⁝ 3 và 69 nên 123 ⁝ 3 và 1239

+) Xét số 2 019 có tổng các chữ số 2 + 0 + 1 + 9 = 12, vì 12 ⁝ 3 và 129 nên 2 019 ⁝ 3 và

2 0199

+) Xét số 2 025 có tổng các chữ số 2 + 0 + 2 + 5 = 9, vì 9 ⁝ 3 và 9 ⁝ 9 nên 2 025 ⁝ 3 và 20 25 ⁝ 9

2 025 ⁝ 9.

Vậy các số chia hết cho 3 là: 450; 123; 2 019; 2 025

        các số chia hết cho 9 là: 450; 2 025.

Bài 2.12 trang 37 Toán lớp 6 Tập 1: Khối lớp 6 của một trường có 290 học sinh đi dã ngoại. Cô phụ trách muốn chia đều số học sinh của khối 6 thành 9 nhóm. Hỏi cô chia nhóm được như vậy không?

Lời giải:

Tổng các chữ số của số 290 là 2 + 9 + 0 =11 không chia hết cho 9 nên 290 không chia hết cho 9. Do đó mà cô không thể chia đều 290 học sinh đi dã ngoại thành 9 nhóm.

Vậy không thể chia đều số học sinh của khối 6 thành 9 nhóm.

Bài 2.13 trang 37 Toán lớp 6 Tập 1: Có 162 học sinh tham gia chương trình đào tạo bóng đá, được chia thành các đội. Mỗi đội cần có 9 học sinh. Hỏi có đội nào không đủ 9 học sinh hay không?

Lời giải:

Tổng các chữ số của 162 là 1 + 6 + 2 = 9 chia hết cho 9 nên 162 chia hết cho 9. Do đó chia 162 em học sinh thành các đội, thì không có đội nào không đủ 9 học sinh.

Bài 2.14 trang 37 Toán lớp 6 Tập 1: Thay dấu * bởi một chữ số để số :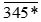

a) Chia hết cho 2

b) Chia hết cho 3

c) Chia hết cho 5

d) Chia hết cho 9.

Lời giải:

Điều kiện * ∈ N, 0 ≤ * ≤ 9

a) Số 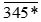chia hết cho 2 thì nó phải có tận cùng là chữ số chẵn nên * ∈ {0;2;4;6;8}

Vậy có thể thay * bằng các chữ số: 0; 2; 4; 6; 8

b) Số 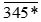 chia hết cho 3 thì tổng các chữ số của nó cũng chia hết cho 3.

Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 3.

Mà 12 chia hết cho 3 nên * cũng phải chia hết cho 3 nên * ∈ {0;3;6;9}

Vậy có thể thay * bằng các chữ số: 0; 3; 6; 9

c) Số 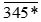 chia hết cho 5 thì nó phải có tận cùng là 0 hoặc 5 nên * ∈ {0;5}

Vậy có thể thay * bằng các chữ số: 0 ; 5

d) Số 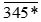chia hết cho 9 thì tổng các chữ số của nó cũng chia hết cho 9

Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 9 nên * ∈ {6}

Vậy có thể thay * bằng chữ số 6.

Bài 2.15 trang 37 Toán lớp 6 Tập 1: Dùng 3 chữ số 3, 0, 4 hãy viết các số tự nhiên có ba chữ số khác nhau và thỏa mãn một trong hai điều kiện:

a) Các số đó chia hết cho 2

b) Các số đó chia hết cho 5

Lời giải:

a) Vì số cần tìm là số tự nhiên chia hết cho 2 nên số cần tìm có chữ số tận cùng là 0 hoặc 4. 

+) Với chữ số tận cùng là 0 và có ba chữ số khác nhau ta được số cần tìm là: 340; 430.

+) Với chữ số tận cùng là 4, chữ số 0 không thể đứng đầu nên số 0 ở hàng chục và số tự nhiên có ba chữ số khác nhau nên ta được số cần tìm là: 304

Vậy các số chia hết cho 2 là:  304; 340; 430.

b) Vì số cần tìm là số tự nhiên chia hết cho 5 nên số cần tìm có chữ số tận cùng là 0. 

Vì số tự nhiên có ba chữ số khác nhau nên ta viết được các số: 340; 430

Vậy các số chia hết cho 5:  340; 430.

Bài 2.16 trang 37 Toán lớp 6 Tập 1: Từ các chữ số 5, 0, 4, 2 viết các số tự nhiên có ba chữ số khác nhau sao cho mỗi số đó chia hết cho 3.

Lời giải:

5 + 4 + 0 = 9 

4 + 2 + 0 = 6

Bộ ba chữ số khác nhau có tổng của chúng chia hết cho 3 là: (5; 4; 0) và (4; 2; 0)

+) Với bộ ba chữ số (5; 4; 0) ta được các số tự nhiên có ba chữ số khác nhau là: 504; 540; 405; 450

+) Với bộ ba chữ số (2; 4; 0) ta được các số tự nhiên có ba chữ số khác nhau là: 420; 402; 240; 204.

Vậy các số cần tìm là: 504; 540; 405; 450; 420; 402; 240; 204.

Xem thêm các bài giải Toán lớp 6 Kết nối tri thức hay, chi tiết khác:

Giải Toán lớp 6 trang 34 Tập 1

Giải Toán lớp 6 trang 35 Tập 1

Giải Toán lớp 6 trang 36 Tập 1