Sử dụng:

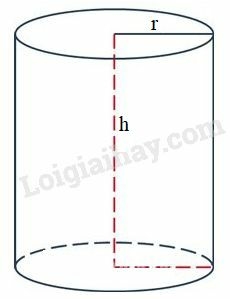
- Công thức tính diện tích xung quanh hình trụ: $S_{xq}=2\pi rh$

- Công thức tính thể tích hình trụ: $V=Sh=\pi r^{2}h$

($r$ là bán kính đường tròn đáy, $h$ là chiều cao, $S$ là diện tích đáy).

Lời giải:

Theo bài ra ta có: $AB+AD=3a;$ $AB.AD=2a^2$ nên độ dài $AB$ và $AD$ là nghiệm của phương trình:

$x^2-3ax+2a^2=0(AB>AD>0)$

$\mathrm{\Delta }={\left(-3a\right)}^2-\mathrm{4.1.2}{a}^2=9a^2-8a^2$$=a^2>0$ (vì $a>0$)

${\displaystyle \Rightarrow x_1=\frac{3a+a}{2}=2a;}$ ${\displaystyle x_2=\frac{3a-a}{2}=a}$

Vì $AB>AD$ nên $AB=2a;AD=a.$

Diện tích xung quanh hình trụ là:

$S=2\pi rh$$=2\pi .AD.AB=2\pi .a.2a$$=4\pi a^2$ (đơn vị diện tích)

Thể tích của hình trụ là:

$V=\pi r^{2}h$$=\pi .A{D}^2.AB=\pi a^2.2a$$=2\pi a^3$ (đơn vị thể tích).

(Lấy ${\displaystyle \pi =\frac{22}{7}}$)

(A) $564c{m}^2$;                  (B) $972c{m}^2$;

(C) $1865c{m}^2$;                (D) $2520c{m}^2$; 

(E) $1496c{m}^2$.

Phương pháp giải:

Sử dụng:

- Công thức tính diện tích xung quanh hình trụ: $S_{xq}=2\pi rh$

($r$ là bán kính đường tròn đáy, $h$ là chiều cao, $S$ là diện tích đáy).

- Công thức tính diện tích hình tròn: $S=\pi r^2$

($r$ là bán kính đường tròn).

Lời giải:

Diện tích xung quanh lọ là: $S_{xq}=2\pi rh$

${\displaystyle S_{xq}=2.\frac{22}{7}.14.10=880(c{m}^2)}$

Diện tích đáy lọ là: $S=\pi r^2$

${\displaystyle S=\frac{22}{7}{.14}^2=616(c{m}^2)}$

Diện tích xung quanh cộng với diện tích một đáy là:

$880+616=1496(c{m}^2)$.

Chọn (E).

a) Diện tích xung quanh của hình trụ.

b) Thể tích của hình trụ.

(Lấy $\pi \approx 3,142$ làm tròn kết quả đến hàng đơn vị).

Phương pháp giải:

Sử dụng:

- Công thức tính diện tích xung quanh hình trụ: $S_{xq}=2\pi rh$

- Công thức tính thể tích hình trụ: $V=Sh=\pi r^{2}h$

($r$ là bán kính đường tròn đáy, $h$ là chiều cao, $S$ là diện tích đáy).

Lời giải:

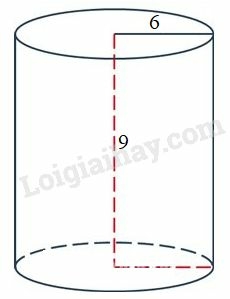
a) Diện tích xung quanh hình trụ là:

$S_{xq}=2\pi rh$

$S_{xq}=2.3,\mathrm{142.6.9}\approx 339(c{m}^2)$

b) Thể tích hình trụ là:

$V=\pi r^{2}h$

$V=3,{142.6}^2.9\approx 1018(c{m}^3)$.

Phương pháp giải:

Sử dụng:

- Công thức tính chu vi đường tròn: $C=2\pi r=\pi d$

($r$ là bán kính đường tròn, $d$ là đường kính).

Lời giải:

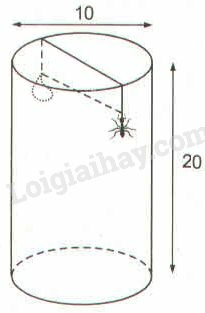
Khai triển hình trụ theo một đường sinh và trải phẳng ra, ta được một hình chữ nhật chiều rộng $20cm$, chiều dài bằng chu vi đáy của cái lọ bằng $10.3,14=31,4(cm).$

Ta cần chú ý đến vị trí con kiến và giọt mật. Ta cho con kiến ở điểm $A$ cách đáy $17cm$, thì giọt mật ở điểm $B$ cũng cách đáy $17cm$ và cách con kiến ở điểm $A$ là nửa chu vi đáy của cái lọ bằng $15,7cm.$

Dựng điểm $C$ đối xứng với $B$ qua đường $xy$, nối $AC$ cắt $xy$ tại $D$. Điểm $D$ là điểm con kiến bò qua.

Vậy đoạn đường $BDA$ là ngắn nhất.

Khi đó quãng đường con kiến cần đi là: $BD+DA=2DA=AC$

Tam giác $ABC$ vuông tại $B$, theo định lý Pi - ta - go ta có:

$A{C}^2=A{B}^2+B{C}^2$ $=15,7^2+6^2$ $\Rightarrow AC=\sqrt{15,7^2+6^2}\approx 16,8\left(cm\right)$

(A) $2(\pi r^2+2\pi rb)c{m}^2$;

(B) $(\pi r^2+2\pi rb)c{m}^2$;

(C) $(2\pi r^2+2\pi rb)c{m}^2$;

(D) $(\pi r^2+4\pi rb)c{m}^2$.

Hãy chọn kết quả đúng.

Phương pháp giải:

Sử dụng:

- Công thức tính diện tích xung quanh hình trụ: $S_{xq}=2\pi rh$.

($r$ là bán kính đường tròn đáy, $h$ là chiều cao).

- Công thức tính diện tích hình tròn: $S=\pi r^2$.

($r$ là bán kính đường tròn).

Lời giải:

Diện tích xung quanh ống hình trụ là: $S_{xq}=2\pi rb(c{m}^2)$

Diện tích đáy của ống hình trụ là: $S=\pi r^2(c{m}^2)$

Diện tích ống được bao phủ bởi lớp sơn bằng hai lần diện tích xung quanh và hai lần diện tích đáy, do đó diện tích ống được sơn bao phủ là:

$2(\pi r^2+2\pi rb)c{m}^2$.

Chọn (A).

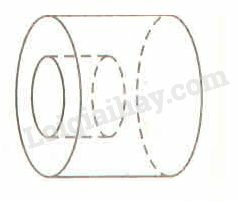
Thể tích phần vật thể  còn lại (tính theo $c{m}^3$) là:

(A) $4\pi r^3$;                      (B) $7\pi r^3$;

(C) $8\pi r^3$;                      (D) $9\pi r^3$.

Hãy chọn kết quả đúng.

Phương pháp giải:

Sử dụng:

- Công thức tính thể tích hình trụ: $V=Sh=\pi r^{2}h$

($r$ là bán kính đường tròn đáy, $h$ là chiều cao, $S$ là diện tích đáy).

Lời giải:

Thể tích vật thể hình trụ là: $V_1=\pi {\left(2r\right)}^2.2r=8\pi r^3(c{m}^3)$

Thể tích lỗ khoan hình trụ là: $V_2=\pi r^2.r=\pi r^3(c{m}^3)$

Thể tích vật thể còn lại là: $V=V_1-V_2=7\pi r^3(c{m}^3)$.

Chọn (B).

Khối lượng của mẩu pho mát là:

(A) $100g$;                   (B) $100\pi g$;

(C) $800g$;                   (D) $800\pi g$.

(Khối lượng riêng của pho mát là $3g/c{m}^3$).

Hãy chọn kết quả đúng.

Phương pháp giải:

Sử dụng:

- Công thức tính thể tích hình trụ: $V=Sh=\pi r^{2}h$.

($r$ là bán kính đường tròn đáy, $h$ là chiều cao, $S$ là diện tích đáy).

Lời giải:

Thể tích khối pho mát hình trụ là: $V=\pi .{10}^2.8=800\pi (c{m}^3)$

Thể tích mẩu pho mát bằng ${\displaystyle \frac{15}{360}=\frac{1}{24}}$ thể tích khối pho mát.

Khối lượng mẩu pho mát là: ${\displaystyle \frac{1}{24}.800.3=100\pi (g).}$

Chọn (B).

Phương pháp giải:

Sử dụng:

- Công thức tính diện tích xung quanh hình trụ: $S_{xq}=2\pi rh$

- Công thức tính diện tích toàn phần hình trụ: $S_{tp}=S_{xq}+2S_{đ}=2\pi rh+2\pi r^2$

- Công thức tính diện tích đáy hình trụ: $S_{đ}=\pi r^2$ 

($r$ là bán kính đường tròn đáy, $h$ là chiều cao).

Lời giải:

Diện tích toàn phần của hình trụ là: $S_{tp}=S_{xq}+2S_{đ}$

Diện tích của một đáy là:

${\displaystyle S_{đ}=\frac{S_{TP}-S_{xq}}{2}=\frac{14-10}{2}}$$=2(m^2)$

Diện tích đáy là: $S_{đ}=\pi r^2$ 

${\displaystyle \Rightarrow r^2=\frac{S_{đ}}{\pi }\approx \frac{2}{3,14}\approx 0,64(m^2)}$

Suy ra bán kính đáy $r=0,8(m)$

Diện tích xung quanh hình trụ là: $S_{xq}=2\pi rh$.

${\displaystyle \Rightarrow h=\frac{S_{xq}}{2\pi r}=\frac{10}{2.3,14.0,8}}$$\approx 1,99(m)$.

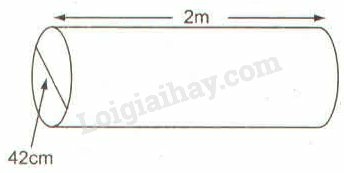
Sau khi lăn trọn $10$ vòng thì trục lăn tạo trên sân phẳng một diện tích là:

(A) $26400c{m}^2$;

(B) $58200c{m}^2$;

(C) $528c{m}^2$;

(D) $264000c{m}^2$.

(Lấy ${\displaystyle \pi =\frac{22}{7}}$).

Hãy chọn kết quả đúng.

Phương pháp giải:

Sử dụng: Công thức tính diện tích xung quanh hình trụ: $S_{xq}=2\pi rh=\pi dh$.

($r,d$ lần lượt là bán kính, đường kính của đường tròn đáy; $h$ là chiều cao).

Lời giải:

Trục lăn một một vòng nên trên sân phẳng một diện tích bằng diện tích xung quanh của trục.

Đổi $2m=200cm.$

Diện tích xung quanh của trục lăn là:

${\displaystyle S_{xq}=\pi dh=42.\frac{22}{7}.200=26400(c{m}^2)}$

Trục lăn $10$ vòng có diện tích là $S=10.S_{xq}=10.26400=264000$$(c{m}^2)$.

Chọn (D)

Một cái cốc hình trụ được đổ đầy sữa. Liệu em có thể rót ra đúng một nửa lượng sữa mà không cần phải sử dụng các công dụng cụ hay không?

Phương pháp giải:

Dùng trực quan và suy luận suy ra đáp án.

Lời giải:

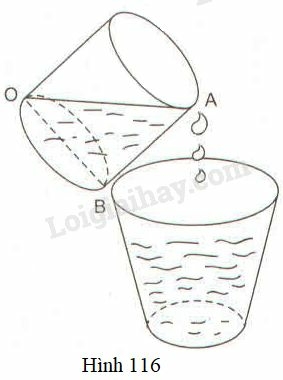
Ta nghiêng cái cốc hình trụ đựng đầy sữa, rót sữa ra vật chứa sữa đến khi sữa trong cốc hình trụ tạo thành góc $AOB$ như hình vẽ thì lượng sữa trong cốc còn đúng một nửa.

Trong các số sau đây, số nào là số biểu diễn khối lượng nước đổ vào thùng?

(A) $165$;                          (B) $16500$;

(C) $33000$;                      (D) $66000$.

(Lấy ${\displaystyle \pi =\frac{22}{7}}$ và kết quả tính theo kilogam).

Phương pháp giải:

Sử dụng: Công thức tính thể tích hình trụ: $V=Sh=\pi r^{2}h$

($r$ là bán kính đường tròn đáy, $h$ là chiều cao, $S$ là diện tích đáy).

Lời giải:

Ta có: ${\displaystyle 2\frac{1}{3}m=\frac{7}{3}m}$.

Thể tích nước chứa trong thùng hình trụ là:

${\displaystyle V=\frac{22}{7}.{\left(\frac{3}{2}\right)}^2.\frac{7}{3}=16,5m^3}$$=16500000(c{m}^3)$.

Khối lượng nước đổ vào thùng là:

$m=16500000.1=16500000(g)$$=16500(kg)$.

Chọn (B).

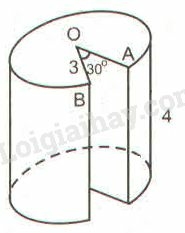
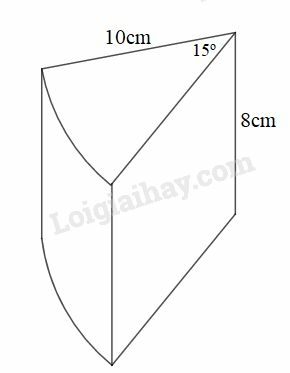
Hãy tính:

a) Thể tích phần còn lại.

b) Diện tích toàn bộ của hình sau khi đã bị cắt.

Phương pháp giải:

Lời giải:

a) Thể tích hình trụ là:

$\begin{array}{l}V=\pi r^2.h\\ V=\pi {.3}^2.4=36\pi (c{m}^3)\end{array}$

Phần hình trụ bị cắt đi bằng  ${\displaystyle \frac{{30}^{\circ }}{{360}^{\circ }}=\frac{1}{12}}$ (hình trụ)

Phần hình trụ còn lại bằng ${\displaystyle 1-\frac{1}{12}=\frac{11}{12}}$ (hình trụ)

Thể tích phần hình trụ còn lại là: ${\displaystyle \frac{11}{12}.36\pi =33\pi (c{m}^3)}$

b) Phần diện tích xung quanh còn lại (không kể phần lõm): $S=2.\pi .3.4.{\displaystyle \frac{11}{12}=22\pi (c{m}^2)}$

Phần diện tích còn lại của $2$ đáy là: ${\displaystyle \pi {.3}^2.\frac{11}{12}.2=\frac{33\pi }{2}(c{m}^2)}$

Diện tích phần lõm là hai hình chữ nhật kích thước $3$ và $4$ là:

$2.(3.4)=24(c{m}^2)$

Diện tích toàn bộ hình sau khi cắt là:

$22\pi +{\displaystyle \frac{33\pi }{2}+24=\left(38\frac{1}{2}\pi +24\right)}$ $(c{m}^2)$.