Câu 1: Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O; R) đường kính BC. Vẽ đường cao AH của tam giác ABC. Đường tròn tâm K đường kính AH cắt AB, AC lần lượt tại D và E. Chọn khẳng định sai:

A. ADHE là hình chữ nhật                

B. AB. AD = AE. AC

C. AH² = AD. AB                             

D. AB. AD = AE. AH

Lời giải:

Xét (O) có 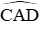 = 90^o (góc nội tiếp chắn nửa đường tròn)

Xét (K) có 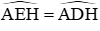 = 90^o (góc nội tiếp chắn nửa đường tròn)

Nên tứ giác ADHE là hình chữ nhật (vì có ba góc vuông) ⇒ Phương án A đúng

Xét tam giác vuông AHB có AH² = AD. AB ⇒ Phương án C đúng

Xét tam giác vuông AH² = AC. AE nên AD. AB = AC. AE ⇒ Phương án B đúng

Đáp án cần chọn là: D

Vận dụng: Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O; R) đường kính BC. Vẽ đường cao AH của tam giác ABC. Đường tròn tâm K đường kính AH cắt AB, AC lần lượt tại D và E. Biết BC = 25cm và AH = 12cm. Hãy tính diện tích xung quanh của hình tạo thành bởi khi cho tứ giác ADHE quay quanh AD.

Lời giải:

Xét tam giác vuông ABC có HB. HC = AH² ⇔ HB. HC = 144 và HB + HC = BC ⇔ HB + HC = 25

Suy ra HB = 9cm; HC = 16cm (chú ý: AB < AC nên HB < HC)

Khi quay hình chữ nhật ADHE quanh AD ta được hình trụ có chiều cao AD, bán kính đáy HD. Nên:

Đáp án cần chọn là: B

Câu 2: Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là 3cm

A. 7cm       

B. 5cm       

C. 3cm       

D. 9cm

Lời giải:

Từ giả thiết ta có 2πRh + 2πR² = 2.2.π.Rh ⇒ Rh = R² ⇒ R = h.

Vậy chiều cao của hình trụ là 3cm

Đáp án cần chọn là: C

Câu 3: Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là 4cm

A. 2cm       

B. 4cm       

C. 1cm       

D. 8cm

Lời giải:

Từ giả thiết ta có 2πRh + 2πR² = 3.2.π.Rh ⇒ 2Rh = R² ⇒ h = 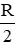 = 2cm

Vậy chiều cao của hình trụ là 2cm

Đáp án cần chọn là: A

Câu 4: Một hình trụ có thể tích V không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất?

Lời giải:

Gọi bán kính đáy và chiều cao của hình trụ lần lượt là R, h (R > 0; h > 0)

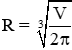
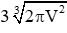
Vậy với   thì S_tp đạt giá trị nhỏ nhất là  

Đáp án cần chọn là: A

Câu 5: Một hình trụ có thể tích 8 cm³ không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất?

Lời giải:

Gọi bán kính đáy và chiều cao của hình trụ lần lượt là R, h (R > 0; h > 0)

Vậy với 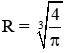  thì S_tp đạt giá trị nhỏ nhất là  

Đáp án cần chọn là: B

Câu 6: Cho hình trụ có bán kính đáy R = 4 (cm) và chiều cao h = 5 (cm). Diện tích xung quanh của hình trụ là:

A. 40π        

B. 30π        

C. 20π        

D. 50π

Lời giải:

Diện tích xung quanh của hình trụ là S_xq = 2πRh = 2π.4.5 = 40π (cm²)

Đáp án cần chọn là: A

Câu 7: Cho hình trụ có bán kính đáy R = 3 (cm) và chiều cao h = 6 (cm). Diện tích xung quanh của hình trụ là:

A. 40π        

B. 36π        

C. 18π        

D. 24π

Lời giải:

Diện tích xung quanh của hình trụ là S_xq = 2πRh = 2π.3.6 = 36π (cm²)

Đáp án cần chọn là: B

Câu 8: Cho hình trụ có chu vi đáy là 8π và chiều cao h = 10. Tính thể tích hình trụ

A. 80π        

B. 40π        

C. 160π      

D. 150π

Lời giải:

Ta có chu vi đáy C = 2πR = 8π  ⇒ R = 4

Thể tích hình trụ là V = πR²h = π.4².10 = 160π  (đvtt)

Đáp án cần chọn là: C

Câu 9: Cho hình trụ có chu vi đáy là 10π và chiều cao h = 11. Tính thể tích hình trụ

A. 55π        

B. 275π      

C. 75π        

D. 150π

Lời giải:

Ta có chu vi đáy C = 2πR = 10π ⇒ R = 5

Thể tích hình trụ là V = πR²h = π.5².11 = 275π  (đvtt)

Đáp án cần chọn là: B

Câu 10: Cho hình trụ có bán kính đáy R = 8cm và diện tích toàn phần 564  cm². Tính chiều cao của hình trụ

A. 27cm     

B. 27,25cm

C. 25cm     

D. 25,27cm

Lời giải:

Đáp án cần chọn là: B

Câu 11: Cho hình trụ có bán kính đáy R = 12 cm và diện tích toàn phần 672π cm². Tính chiều cao của hình trụ

A. 16cm     

B. 18cm     

C. 8cm       

D. 20cm

Lời giải:

Đáp án cần chọn là: A

Câu 12: Cho hình trụ có bán kính đáy R và chiều cao h. Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì

A. Thể tích hình trụ không đổi           

B. Diện tích toàn phần không đổi

C. Diện tích xung quanh không đổi    

D. Chu vi đáy không đổi

Lời giải:

Chiều cao mới của hình trụ là h’ = 2h; bán kính mới là 

Hình trụ mới có:

Chu vi đáy 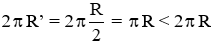 = C nên Phương án D sai

Diện tích toàn phần 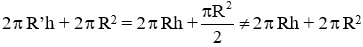 nên Phương án B sai

Thể tích 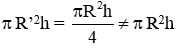 nên Phương án A sai

Diện tích xung quanh 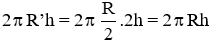 nên Phương án C đúng

Đáp án cần chọn là: C

Câu 13: Chọn câu đúng. Cho hình trụ có bán kính đáy R và chiều cao h. Nếu ta giảm chiều cao đi chín lần và tăng bán kính đáy lên ba lần thì

A. Thể tích hình trụ không đổi           

B. Diện tích toàn phần không đổi

C. Diện tích xung quanh không đổi    

D. Chu vi đáy không đổi

Lời giải:

Chiều cao mới của hình trụ là 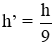; bán kính đáy mới là R’ = 3R

Hình trụ mới có:

Chu vi đáy 2πR’ = 2π.3R = 6πR = 3.2πR = 3C nên phương án D sai

Thể tích 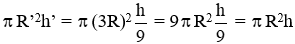 nên phương án A đúng

Diện tích xung quanh 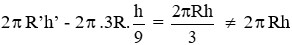 nên phương án C sai

Đáp án cần chọn là: A

Câu 14: Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 12cm và đường kính đáy là d = 8cm. Tính diện tích toàn phần của hộp sữa. Lấy π ≈ 3,14

A. 110π  (cm²)

B. 128π  (cm²)

C. 96π  (cm²)

D. 112π  (cm²)

Lời giải:

Bán kính đường tròn đáy R = 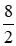 = 4cm nên diện tích một đát S_d = πR² = 16π (cm²)

Ta có diện tích xung quanh của hình trụ S_xq = 2πRh = 2π.4.12 = 96 (cm²)

Vì hộp sữa đã mất nắp nên diện tích toàn phần của hộp sữa

S_tp = 96π + 16π = 112π (cm²)

Đáp án cần chọn là: D

*Chú ý: Một số bạn sẽ tính diện tích toàn phần bằng tổng diện tích xung quanh với diện tích hai đáy nhưng hộp sữa ở đây đã mất nắp nên chỉ còn một đáy. Khi tính ta chỉ cần lấy tổng diện tích xung quanh với diện tích một đáy

Câu 15: Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 10cm và đường kính đáy là d = 6cm. Tính diện tích toàn phần của hộp sữa. Lấy π ≈ 3,14

A. 110π  (cm²)

B. 129π  (cm²)

C. 96π  (cm²)

D. 69π  (cm²)

Lời giải:

Bán kính đường tròn đáy R = 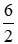 = 3cm nên diện tích một đát S_d = πR² = 9 (cm²)

Ta có diện tích xung quanh của hình trụ S_xq = 2πRh = 2π.3.10 = 60 (cm²)

Vì hộp sữa đã mất nắp nên diện tích toàn phần của hộp sữa

S_tp = 9π + 60π = 69π  (cm²)

Đáp án cần chọn là: D

*Chú ý: Một số bạn sẽ tính diện tích toàn phần bằng tổng diện tích xung quanh với diện tích hai đáy nhưng hộp sữa ở đây đã mất nắp nên chỉ còn một đáy. Khi tính ta chỉ cần lấy tổng diện tích xung quanh với diện tích một đáy

Câu 16: Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy S = 25π cm² và chiều cao h = 10cm. Nếu trục lăn đủ 12 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?

A. 1200  (cm²)                                

B. 600π  (cm²)      

C. 1000π  (cm²)                                

D. 1210π  (cm²)

Lời giải:

Bán kính R của đường tròn đáy là πR² = 25π ⇒  R = 5cm

Diện tích xung quanh của hình trụ S_xq = 2πRh = 2π.5.10 = 100π (cm²)

Vì trục lăn 12 vòng nên diện tích tạo trên sân phẳng là 12.100 = 1200 (cm²)

Đáp án cần chọn là: A

Câu 17: Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy S = 36π cm² và chiều cao h = 8cm. Nếu trục lăn đủ 10 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?

A. 1200π  (cm²)                                

B. 480π  (cm²)      

C. 960π  (cm²)                                  

D. 960 (cm²)

Lời giải:

Bán kính R của đường tròn đáy là πR² = 36π ⇒ R = 6cm

Diện tích xung quanh của hình trụ S_xq = 2πRh = 2π.6.8 = 96π (cm²)

Vì trục lăn 12 vòng nên diện tích tạo trên sân phẳng là 10.96 = 960 (cm²)

Đáp án cần chọn là: C

Câu 18: Cho hình trụ bị cắt bỏ một phần OABB’A’O’ như hình vẽ. Thể tích phần còn lại là:

A. 70π  (cm³)                                    

B. 80π  (cm³)        

C. 60π  (cm³)                                    

D. 10π  (cm³)

Lời giải:

Đáp án cần chọn là: A

Câu 19: Cho hình trụ bị cắt bỏ một phần OABB’A’O’ như hình vẽ. Thể tích phần còn lại là:

A. 187,5π  (cm³)                               

B. 187π  (cm³)      

C. 375π  (cm³)                                  

D. 75π  (cm³)

Lời giải:

Đáp án cần chọn là: A

Bài giảng Toán 9 Bài 1: Hình trụ, diện tích xung quanh và thể tích của hình trụ