Với giải Câu 4 trang 59 Vở bài tập Toán lớp 7 Cánh diều chi tiết trong Bài 5: Phép chia đa thức một biến giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 7. Mời các bạn đón xem:

Giải VBT Toán lớp 7 Bài 5: Phép chia đa thức một biến

• Câu 4 trang 59 vở bài tập Toán lớp 7 Tập 2:

  a) ( 6x² – 2x + 1) : ( 3x – 1 )

  .......................................................................................................................

  ........................................................................................................................

  b) ( 27x³ + x² – x + 1) : ( –2x + 1)

  ........................................................................................................................

  ........................................................................................................................

  c) (8x³ + 2x² + x) : (2x³ + x + 1)

  ........................................................................................................................

  ........................................................................................................................

  d) ( 3x⁴ + 8x³ – 2x² + x + 1) : ( 3x + 1) ........................................................................................................................

  ........................................................................................................................

  Lời giải:

  a) ( 6x² – 2x + 1) : ( 3x – 1 )

  
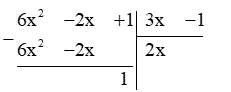
  Vậy (6x² – 2x + 1) : (3x – 1) = 2x ( dư 1).

  b) ( 27x³ + x² – x + 1) : (–2x + 1)

  
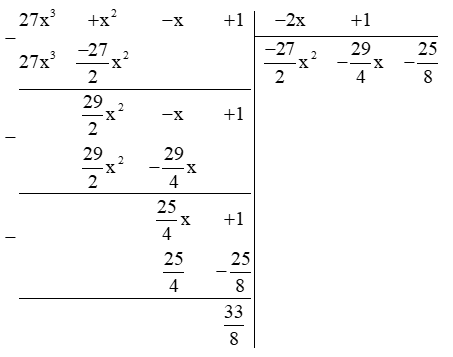
  Vậy ( 27x³ + x² – x + 1) : ( –2x + 1) = $\frac{-27}{2}{\text{x}}^2-\frac{29}{4}\text{x}-\frac{25}{8}$ ( dư $\frac{33}{8}$).

  c) (8x³ + 2x² + x) : (2x³ + x + 1)

  
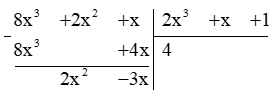
  Vậy (8x³ + 2x² + x) : (2x³ + x + 1) = 4 (dư 2x² – 3x).

  d) ( 3x⁴ + 8x³ – 2x² + x + 1) : ( 3x + 1)

  
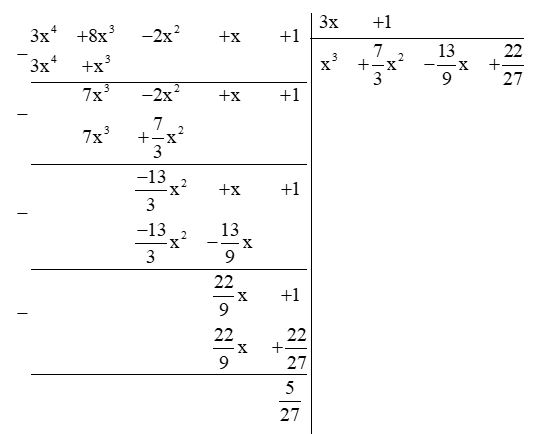
  Vậy ( 3x⁴ + 8x³ – 2x² + x + 1) : ( 3x + 1) = x³ + $\frac{7}{3}$x² – $\frac{13}{9}$x + $\frac{22}{7}$ (dư $\frac{5}{27}$).