Với Giải toán lớp 7 trang 119 Tập 2 Cánh diều tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải Toán 7 trang 119 Tập 2 Cánh diều

Bài 1 trang 119 Toán 7 Tập 2: Cho tam giác ABC có: $\widehat{A}=42°,\widehat{B}=37°.$

a) Tính $\widehat{C}$.

b) So sánh độ dài các cạnh AB, BC, CA.

Lời giải:

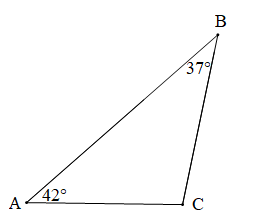
a) Xét tam giác ABC: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (tổng ba góc trong một tam giác)

Suy ra $\widehat{C}=180°-\widehat{A}-\widehat{B}=180°-42°-37°=101°$.

Vậy $\widehat{C}=101°.$ 

b) Ta có: 37° < 42° < 101° nên $\widehat{B}<\widehat{A}<\widehat{C}$.

Do đó CA < BC < AB (quan hệ giữa góc và cạnh đối diện)

Vậy CA < BC < AB.

Bài 2 trang 119 Toán 7 Tập 2: Tìm các số đo x, y trong Hình 140.

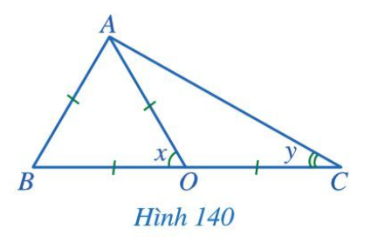
Lời giải:

Xét tam giác ABO có OA = AB = BO nên tam giác ABO đều.

Do đó x = 60°.

Tam giác OAC có OA = OC nên tam giác OAC cân tại O.

Do đó $y=\widehat{OAC}=\widehat{OAC}$.

Ta có $\widehat{AOB}$ là góc ngoài tại đỉnh O của $∆$OAC nên $\widehat{AOB}=\widehat{OCA}+\widehat{OAC}$.

hay x = y + y = 2y.

Suy ra 2y = 60°

Do đó y = 30°.

Vậy x = 60° và y = 30°.

Bài 3 trang 119 Toán 7 Tập 2: Bạn Hoa đánh dấu ba vị trí A, B, C trên một phần sơ đồ xe buýt ở Hà Nội năm 2021 và xem xe buýt có thể đi như thế nào giữa hai vị trí A và B. Đường thứ nhất đi từ A đến C và đi tiếp từ C đến B, đường thứ hai đi từ B đến A (Hình 141). Theo em, đường nào đi dài hơn? Vì sao?

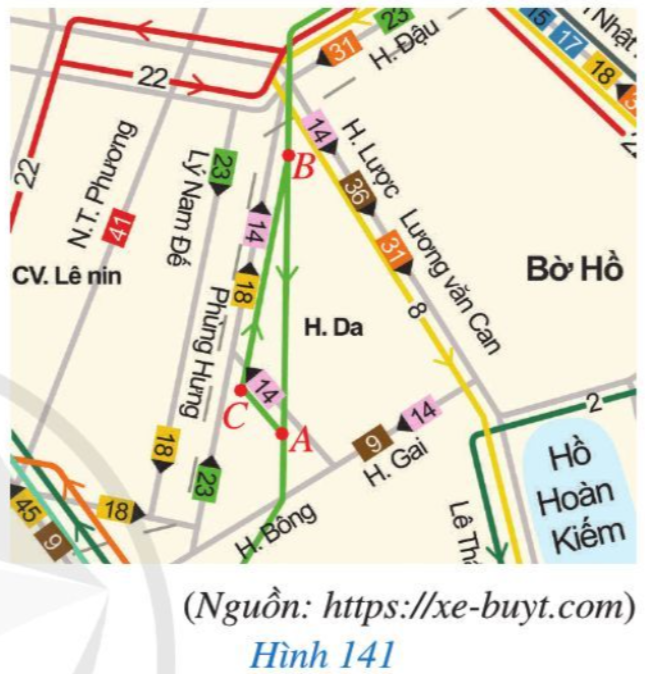
Lời giải:

Ba vị trí A, B, C mà bạn Hoa đánh dấu tạo thành ba đỉnh của tam giác ABC (Hình 141).

Khi đó trong tam giác ABC ta có: AC + CB > BA (Bất đẳng thức tam giác)

Vậy đường thứ nhất dài hơn đường thứ hai.

Bài 4 trang 119 Toán 7 Tập 2: Cho hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM. Gọi I và K lần lượt là trung điểm của BC và NP. Chứng minh: AI = MK.

Lời giải:

Chứng minh (Hình vẽ dưới đây):

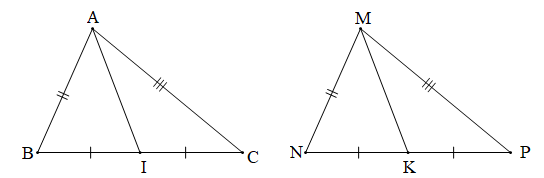
Xét $∆$ABC và $∆$MNP có:

AB = MN (giả thiết).

BC = NP (giả thiết).

CA = PM (giả thiết).

Do đó $∆$ABC = $∆$MNP  (c.c.c).

Suy ra $\widehat{ABC}=\widehat{MNP}$.

Do I, K lần lượt là trung điểm của BC và NP nên $BI=IC=\frac{1}{2}BC$ và $NK=KP=\frac{1}{2}NP$ 

Mà BC = NP (giả thiết) nên BI = NK.

Xét $∆$ABI và $∆$MNK có:

AB = MN (giả thiết).

$\widehat{ABI}=\widehat{MNK}$ (chứng minh trên).

BO = NK (chứng minh trên).

Do đó $∆$ABI = $∆$MNK (c.g.c).

Suy ra AI = MK (hai cạnh tương ứng).

Vậy AI = MK.

Bài 5 trang 119 Toán 7 Tập 2: Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N.

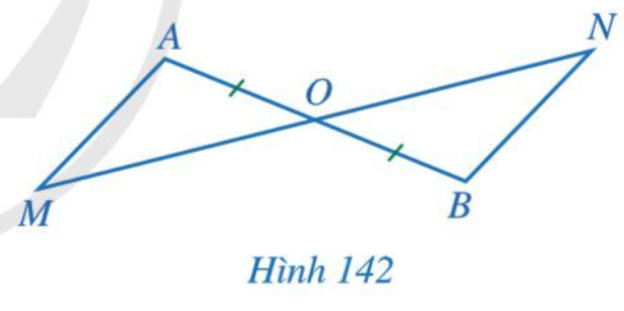
Chứng minh:

a) Nếu OM = ON thì AM // BN;

b) Nếu AM // BN thì OM = ON.

Lời giải:

a)

Chứng minh (Hình 142):

Xét $∆$OAM và $∆$OBN có:

AO = BO (do M là trung điểm của AB),

$\widehat{AOM}=\widehat{BON}$ (hai góc đối đỉnh),

OM = ON (giả thiết).

Do đó $∆$OAM = $∆$OBN (c.g.c).

Suy ra $\widehat{AM\text{O}}=\widehat{BNO}$ (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong nên AM // BN (dấu hiệu nhận biết)

Vậy AM //BN.

b)

Chứng minh (Hình 142):

Do AM // BN (giả thiết) nên $\widehat{MAO}=\widehat{NBO}$ (hai góc so le trong).

Xét $∆$OAM và $∆$OBN có:

$\widehat{MAO}=\widehat{NBO}$ (chứng minh trên),

AO = BO (do M là trung điểm của AB),

$\widehat{AOM}=\widehat{BON}$ (hai góc đối đỉnh).

Do đó $∆$OAM = $∆$OBN (g.c.g).

Suy ra OM = ON (hai cạnh tương ứng).

Vậy OM = ON.

Bài 6 trang 119 Toán 7 Tập 2: Cho tam giác ABC cân tại A có

$\widehat{ABC}=70°$. Hai đường cao BD và CE cắt nhau tại H.

a) Tính số đo các góc còn lại của tam giác ABC.

b) Chứng minh BD = CE.

c) Chứng minh tia AH là tia phân giác của góc BAC.

Lời giải:

Chứng minh (Hình vẽ dưới đây):

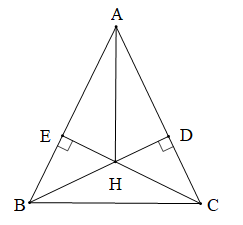
a) Do tam giác ABC cân tại A (giả thiết)

Nên AB = AC và $\widehat{ABC}=\widehat{ACB}=70°$ (tính chất tam giác cân)

Xét tam giác ABC có $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$ (tổng ba góc trong tam giác)

Suy ra $\widehat{BAC}=180°-\widehat{ABC}-\widehat{ACB}=180°-70°-70°=40°$.

Vậy $\widehat{ACB}=70°$ và $\widehat{BAC}=40°.$ 

b) Xét $∆$ADB (vuông tại D) và $∆$ACE (vuông tại E) có:

AB = AC (chứng minh trên),

$\widehat{A}$ là góc chung,

Do đó $∆$ABD = $∆$ACE (cạnh huyền - góc nhọn).

Suy ra BD = CE (hai cạnh tương ứng).

Vậy BD = CE.

c) Vì $∆$ABD = $∆$ACE (chứng minh câu a) nên AD = AE (hai cạnh tương ứng).

Xét $∆$AHE (vuông tại E) và $∆$AHD (vuông tại D) có:

AE = AD (chứng minh trên),

AH là cạnh chung.

Do đó $∆$AHE  = $∆$AHD (cạnh huyền - cạnh góc vuông).

Suy ra $\widehat{HA\text{E}}=\widehat{HA\text{D}}$ (hai góc tương ứng).

Do đó AH là tia phân giác của $\widehat{EAD}$.

Vậy AH là tia phân giác của $\widehat{BAC}$.

Bài 7 trang 119 Toán 7 Tập 2: Cho hai tam giác nhọn ABC và ECD, trong đó ba điểm B, C, D thẳng hàng. Hai đường cao BM và CN của tam giác ABC cắt nhau tại I, hai đường cao CP và DQ của tam giác ECD cắt nhau tại K (Hình 143). Chứng minh AI // EK.

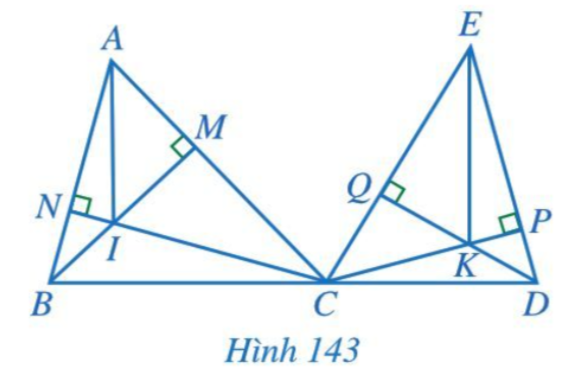
Lời giải:

Chứng minh (Hình 143):

Vì $∆$ABC có hai đường cao BM và CN cắt nhau tại I (giả thiết) nên I là trực tâm của $∆$ABC.

Suy ra AI $\perp$ BC.

Vì $∆$ECD có hai đường cao CP và DQ cắt nhau tại K (giả thiết) nên K là trực tâm của $∆$ECD.

Suy ra EK $\perp$ CD.

Mà B, C, D thẳng hàng (giả thiết) nên

• AI $\perp$ BC (chứng minh trên)  suy ra AI $\perp$ BD;

• EK $\perp$ CD (chứng minh trên) suy ra EK $$ BD.

Do đó AI // EK (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì hai đường thẳng đó song song)

Vậy AI // EK.

Xem thêm các bài giải Toán lớp 7 Cánh diều hay, chi tiết khác:

Giải Toán 7 trang 120 Tập 2