Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi hai số cần tìm là $x$ và $y$.

Vì tổng của hai số bằng $59$ nên ta có phương trình: $x+y=59$

Vì hai lần của số này bé hơn ba lần của số kia là $7$ nên ta có phương trình: $3y–2x=7$

Khi đó ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}x+y=59\\ 3y-2x=7\end{array}\iff \{\begin{array}{c}2x+2y=118\\ -2x+3y=7\end{array}\\ & \iff \{\begin{array}{c}5y=125\\ x+y=59\end{array}\iff \{\begin{array}{c}y=25\\ x+25=59\end{array}\\ & \iff \{\begin{array}{c}y=25\\ x=34\end{array}\end{array}$

Vậy hai số phải tìm là $34$ và $25.$

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi tuổi mẹ năm nay là $x$, tuổi con năm nay là $y.$

Điều kiện: $x,y\in {\mathbb{N}}^{\ast };x>y>7.$

Năm nay tuổi mẹ gấp ba lần tuổi con nên ta có phương trình: $x=3y$

Bảy năm trước, tuổi của mẹ là $(x-7)$ tuổi và tuổi con là $(y-7)$ tuổi.

Vì bảy năm trước tuổi mẹ bằng năm lần tuổi con cộng thêm $4$ nên ta có phương trình:

$x–7=5(y–7)+4\iff x-5y=-24$

Khi đó ta có hệ phương trình: 

$\begin{array}{rl}& \{\begin{array}{c}x=3y\\ x-5y=-24\end{array}\\ & \iff \{\begin{array}{c}x=3y\\ 3y-5y=-24\end{array}\\ & \iff \{\begin{array}{c}x=3y\\ y=12\end{array}\\ & \iff \{\begin{array}{c}x=36\\ y=12\end{array}\end{array}$

Ta thấy $x=36,y=12$ thỏa mãn điều kiện  $x,y\in {\mathbb{N}}^{\ast };x>y>7.$

Vậy năm nay mẹ $36$ tuổi, con $12$ tuổi.

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

- Biểu diễn số có hai chữ số: 

$\overline{xy}=10x+y$ $(x,y\in \mathbb{N}$  và $0<x\le 9;$ $0\le y\le 9)$

Lời giải:

Gọi chữ số hàng chục của số đã cho là $x$, chữ số hàng đơn vị là $y.$

Điều kiện: $x,y\in {\mathbb{N}}^{\ast },x\le 9,y\le 9$

Khi đó số đã cho $\overline{xy}=10x+y$.

Nếu đổi chỗ hai chữ số của số đã cho ta được số mới là $\overline{yx}=10y+x$

Do số mới lớn hơn số đã cho là $63$ nên ta có phương trình:

$\overline{yx}-\overline{xy}=63$

$$\begin{gathered} \iff \left(10y+x\right)-\left(10x+y\right)=63 \\ \iff 9y-9x=63 \\ \iff -x+y=7 \end{gathered}$$

Mà tổng của số mới và số đã cho bằng $99$ nên ta có phương trình:

$\overline{yx}+\overline{xy}=99$

$$\begin{gathered} \iff \left(10x+y\right)+\left(10y+x\right)=99 \\ \iff 11x+11y=99 \\ \iff x+y=9 \end{gathered}$$

Khi đó ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}-x+y=7\\ x+y=9\end{array}\iff \{\begin{array}{c}2y=16\\ x+y=9\end{array}\\ & \iff \{\begin{array}{c}y=8\\ x+8=9\end{array}\iff \{\begin{array}{c}y=8\\ x=1\end{array}\end{array}$

Ta thấy $x=1;y=8$ thỏa mãn điều kiện $x,y\in {\mathbb{N}}^{\ast },x\le 9,y\le 9$.

Vậy số đã cho là $18.$

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi số tiền lãi mà anh Quang được hưởng là $x$ (triệu đồng), anh Hùng được hưởng là $y$ ( triệu đồng).

Điều kiện: $0<x<7;0<y<7$

Do số tiền lãi cả hai anh được hưởng là $7$ triệu đồng nên ta có phương trình:

$x+y=7$

Mà số tiền lãi tỉ lệ với vốn đã góp nên ta có phương trình: ${\displaystyle \frac{x}{15}=\frac{y}{13}}$

Khi đó ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}x+y=7\\ {\displaystyle \frac{x}{15}=\frac{y}{13}}\end{array}\\ & \iff \{\begin{array}{c}x+y=7\\ x={\displaystyle \frac{15y}{13}}\end{array}\\ & \iff \{\begin{array}{c}{\displaystyle \frac{15y}{13}+y=7}\\ x={\displaystyle \frac{15y}{13}}\end{array}\\ & \iff \{\begin{array}{c}15y+13y=91\\ x={\displaystyle \frac{15y}{13}}\end{array}\\ & \iff \{\begin{array}{c}28y=91\\ x={\displaystyle \frac{15y}{13}}\end{array}\\ & \iff \{\begin{array}{c}y=3,25\\ x={\displaystyle \frac{15.3,25}{13}}\end{array}\\ & \iff \{\begin{array}{c}y=3,25\\ x=3,75\end{array}\end{array}$

Giá trị $x=3,75;y=3,25$ thỏa mãn điều kiện bài toán.

Vậy anh Quang  được hưởng $3750000$ đồng tiền lãi; anh Hùng được hưởng $3250000$ đồng tiền lãi.

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi giá của một quả trứng gà là $x$ (đồng), giá của một quả trứng vịt là $y$ (đồng).

Điều kiện: $x>0;y>0$

Hôm qua mẹ Lan mua năm quả trứng gà và năm quả trứng vịt hết $10000$ đồng nên ta có phương trình:

$5x+5y=10000$

Hôm nay mẹ Lan mua ba quả trứng gà và bảy quả trứng vịt  hết $9600$ đồng nên  ta có phương trình:

$3x+7y=9600$

Khi đó ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}5x+5y=10000\\ 3x+7y=9600\end{array}\\ & \iff \{\begin{array}{c}x+y=2000\\ 3x+7y=9600\end{array}\\ & \iff \{\begin{array}{c}3x+3y=6000\\ 3x+7y=9600\end{array}\\ & \iff \{\begin{array}{c}4y=3600\\ x+y=2000\end{array}\\ & \iff \{\begin{array}{c}y=900\\ x+900=2000\end{array}\\ & \iff \{\begin{array}{c}y=900\\ x=1100\end{array}\end{array}$

Ta thấy $x=1100$ và $y=900$ thỏa mãn điều kiện bài toán.

Vậy giá một quả trứng gà là $1100$ đồng; giá một quả trứng vịt là $900$ đồng.

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn:

Bước 1: Lập hệ phương trình

 + Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

 + Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

 + Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

- Chu vi hình chữ nhật bằng hai lần tổng của chiều dài và chiều rộng.

Lời giải:

Gọi chiều rộng của sân trường là $x(m)$, chiều dài của sân trường là $y(m).$

Điều kiện: $0<x<y<170$

Vì chu vi của sân trường bằng $340m$ nên ta có phương trình:

$\left(x+y\right).2=340\iff x+y=170$

Ba lần chiều dài hơn bốn lần chiều rộng là $20m$  nên ta có phương trình: $3y–4x=20$

Khi đó ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}x+y=170\\ 3y-4x=20\end{array}\\ & \iff \{\begin{array}{c}4x+4y=680\\ -4x+3y=20\end{array}\\ & \iff \{\begin{array}{c}7y=700\\ x+y=170\end{array}\\ & \iff \{\begin{array}{c}y=100\\ x+100=170\end{array}\\ & \iff \{\begin{array}{c}y=100\\ x=70\end{array}\end{array}$

Cả hai giá trị $x=70;y=100$ thỏa mãn điều kiện bài toán.

Vậy chiều rộng của sân là $70m$, chiều dài của sân là $100m.$

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn:

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi giá tiền của $1kg$ sắt $\varnothing 8$ là $x$ (đồng) và khoản tiền chi cho trần tầng một là $y$ (đồng).

Điều kiện: $x>0;y>0$

Vì giá tiền một cây sắt $\varnothing 18$ đắt gấp $22$ lần giá tiền $1kg$  sắt $\varnothing 8$ nên giá tiền một cây sắt $\varnothing 18$ là $22x$ (đồng).

Trần tầng một dùng $30$ cây sắt $\varnothing 18$ và $350kg$ sắt $\varnothing 8$ hết $y$ đồng nên ta có phương trình:

$30.22x+350x=y$

Trần tầng hai dùng $20$ cây sắt $\varnothing 18$ và $250kg$  sắt $\varnothing 8$ hết một khoản tiền ít hơn khoản tiền chi cho trần tầng một là $1440000$ đồng nên ta có phương trình:

$20.22x+250x=y–1440000$

Khi đó ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}30.22x+350x=y\\ 20.22x+250x=y-1440000\end{array}\\ & \iff \{\begin{array}{c}1010x=y\\ 690x=y-1440000\end{array}\\ & \iff \{\begin{array}{c}1010x=y\\ 690x=1010x-1440000\end{array}\\ & \iff \{\begin{array}{c}1010x=y\\ 320x=1440000\end{array}\\ & \iff \{\begin{array}{c}1010x=y\\ x=4500\end{array}\\ & \iff \{\begin{array}{c}y=4545000\\ x=4500\end{array}\end{array}$

Ta thấy $x=4500;y=4545000$ thỏa mãn điều kiện bài toán.

Vậy giá $1kg$ sắt $\varnothing 8$ là $4500$ đồng; giá một cây sắt $\varnothing 18$ bằng $4500.22=99000$ đồng.

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi số ghế trong phòng học là $x$ (ghế), số học sinh của lớp là $y$ (học sinh)

Điều kiện: $x,y\in {\mathbb{N}}^{\ast }$

Nếu xếp mỗi ghế ba học sinh thì số học sinh được ngồi ghế là $3x$ và có $6$ học sinh không có chỗ nên ta có phương trình: $3x+6=y$

Nếu xếp mỗi ghế bốn học sinh thì thừa $1$ ghế không có học sinh ngồi nên số học sinh được ngồi ghế là $(x-1).4$, ta có phương trình: $(x–1).4=y$ 

Khi đó ta có hệ phương trình: 

$\begin{array}{rl}& \{\begin{array}{c}3x+6=y\\ \left(x-1\right).4=y\end{array}\iff \{\begin{array}{c}3x-y=-6\\ 4x-y=4\end{array}\\ & \iff \{\begin{array}{c}x=10\\ 4x-y=4\end{array}\\ & \iff \{\begin{array}{c}x=10\\ y=4x-4\end{array}\iff \{\begin{array}{c}x=10\\ y=36\end{array}\end{array}$

Ta thấy $x=10$ và $y=36$ thỏa mãn điều kiện bài toán.

Vậy phòng học có $10$ ghế và lớp có $36$ học sinh.

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi năng suất trên một ha của lúa giống mới là $x$ ( tấn), của lúa giống cũ là $y$ (tấn).

Điều kiện: $x>0;y>0$

Do trên cánh đồng cấy $60$ ha lúa giống mới và $40$ ha lúa giống cũ thu hoạch được tất cả $460$ tấn thóc nên ta có phương trình: $60x+40y=460$

Mà $3$ ha trồng lúa mới thu hoạch được ít hơn $4$ ha trồng lúa cũ là $1$ tấn nên ta có phương trình:

$4y–3x=1$

Khi đó ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}60x+40y=460\\ 4y-3x=1\end{array}\\ & \iff \{\begin{array}{c}6x+4y=46\\ -6x+8y=2\end{array}\\ & \iff \{\begin{array}{c}12y=48\\ 4y-3x=1\end{array}\\ & \iff \{\begin{array}{c}y=4\\ 4.4-3x=1\end{array}\\ & \iff \{\begin{array}{c}y=4\\ x=5\end{array}\end{array}$

Giá trị $x=5;y=4$ thỏa mãn điều kiện bài toán.

Vậy năng suất trên $1$ ha của lúa giống mới là $5$ tấn, năng suất trên $1$ ha của lúa giống cũ là $4$ tấn.

Phương pháp giải:

Sử dụng:

- Xem toàn bộ công việc là $1$ (công việc)

- Thực hiện một công việc trong $a$ (giờ) $(a>0)$ thì xong việc.

Suy ra trong một giờ thực hiện được ${\displaystyle \frac{1}{a}}$ công việc

- Cách giải bài toán bằng cách lập hệ phương trình:

Bước $1$: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng 

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước $2$: Giải hệ phương trình nói trên (sử dụng phương pháp đặt ẩn số phụ)

Bước $3$: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Đổi $7$ giờ $12$ phút $={\displaystyle \frac{36}{5}}$ giờ

Gọi thời gian người thứ nhất xây một mình xong bức tường là $x$ ( giờ), thời gian người thứ hai xây một mình xong bức tường là $y$ (giờ)

Điều kiện: $x>{\displaystyle \frac{36}{5};y>\frac{36}{5}}$

Trong $1$ giờ người thứ nhất xây được ${\displaystyle \frac{1}{x}}$ (bức tường)

Trong $1$ giờ người thứ hai xây được ${\displaystyle \frac{1}{y}}$ (bức tường)

Vì hai người thợ cùng xây một bức tường trong $7$ giờ $12$ phút  hay ${\displaystyle \frac{36}{5}}$ giờ thì xong nên trong $1$ giờ cả hai người xây được ${\displaystyle 1:\frac{36}{5}=\frac{5}{36}}$ (bức tường).

Do đó ta có phương trình: ${\displaystyle \frac{1}{x}+\frac{1}{y}=\frac{5}{36}}$

Nếu người thứ nhất làm trong $5$ giờ và người thứ hai làm trong $6$ giờ thì cả hai xây được ${\displaystyle \frac{3}{4}}$ bức tường, khi đó ta có:

${\displaystyle \frac{5}{x}+\frac{6}{y}=\frac{3}{4}}$

Ta có hệ phương trình:

$\{\begin{array}{c}{\displaystyle \frac{1}{x}+\frac{1}{y}=\frac{5}{36}}\\ {\displaystyle \frac{5}{x}+\frac{6}{y}=\frac{3}{4}}\end{array}$

Đặt ${\displaystyle \frac{1}{x}=a;\frac{1}{y}=b(a>0;b>0)}$ ta có:

$\begin{array}{rl}& \{\begin{array}{c}a+b={\displaystyle \frac{5}{36}}\\ 5a+6b={\displaystyle \frac{3}{4}}\end{array}\\ & \iff \{\begin{array}{c}5a+5b={\displaystyle \frac{25}{36}}\\ 5a+6b={\displaystyle \frac{3}{4}}\end{array}\\ & \iff \{\begin{array}{c}b={\displaystyle \frac{1}{18}}\\ a+b={\displaystyle \frac{5}{36}}\end{array}\\ & \iff \{\begin{array}{c}b={\displaystyle \frac{1}{18}}\\ a={\displaystyle \frac{1}{12}}\end{array}\text{(thỏa mãn)}\end{array}$

Suy ra:

$\{\begin{array}{c}{\displaystyle \frac{1}{x}=\frac{1}{12}}\\ {\displaystyle \frac{1}{y}=\frac{1}{18}}\end{array}\iff \{\begin{array}{c}x=12\\ y=18\end{array}\text{(thỏa mãn)}$

Vậy người thứ nhất làm một mình trong $12$ giờ thì xây xong bức tường, người thứ hai làm một mình trong $18$ giờ thì xây xong bức tường.

Phương pháp giải:

Sử dụng:

- Xem toàn bộ công việc là $1$ (công việc)

- Thực hiện một công việc trong $a$ (ngày) $(a>0)$ thì xong việc.

Suy ra trong một ngày thực hiện được ${\displaystyle \frac{1}{a}}$ công việc

- Cách giải bài toán bằng cách lập hệ phương trình:

Bước $1$: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước $2$: Giải hệ phương trình nói trên (sử dụng phương pháp đặt ẩn số phụ)

Bước $3$: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi thời gian người thứ nhất làm một mình xong công việc là $x$ (ngày), thời gian người thứ hai làm một mình xong công việc là $y$ (ngày).

Điều kiện: $x>4;y>4$

Trong $1$ ngày người thứ nhất làm được ${\displaystyle \frac{1}{x}}$ (công việc)

Trong 1 ngày người thứ hai làm được ${\displaystyle \frac{1}{y}}$ (công việc)

Vì hai người làm chung trong bốn ngày thì xong việc nên trong 1 ngày cả hai người làm được $1:4={\displaystyle \frac{1}{4}}$ (công việc)

Do đó ta có phương trình: ${\displaystyle \frac{1}{x}+\frac{1}{y}=\frac{1}{4}}$

Nếu người thứ nhất làm một mình trong chín ngày rồi người thứ hai đến cùng làm tiếp trong một ngày nữa thì xong việc, tức là người thứ nhất làm trong $10$ ngày và người thứ hai làm trong $1$ ngày thì xong công việc. Khi đó ta có phương trình:

 ${\displaystyle \frac{10}{x}+\frac{1}{y}=1}$

Ta có hệ phương trình:

$\{\begin{array}{c}{\displaystyle \frac{1}{x}+\frac{1}{y}=\frac{1}{4}}\\ {\displaystyle \frac{10}{x}+\frac{1}{y}=1}\end{array}$

Đặt ${\displaystyle \frac{1}{x}=a;\frac{1}{y}=b}$$(a>0;b>0)$ 

Khi đó hệ phương trình trên trở thành:

$\begin{array}{rl}& \{\begin{array}{c}a+b={\displaystyle \frac{1}{4}}\\ 10a+b=1\end{array}\\ & \iff \{\begin{array}{c}9a={\displaystyle \frac{3}{4}}\\ a+b={\displaystyle \frac{1}{4}}\end{array}\\ & \iff \{\begin{array}{c}a={\displaystyle \frac{1}{12}}\\ {\displaystyle \frac{1}{12}+b=\frac{1}{4}}\end{array}\\ & \iff \{\begin{array}{c}a={\displaystyle \frac{1}{12}}\\ b={\displaystyle \frac{1}{6}}\end{array}\text{(thỏa mãn)}\end{array}$

Suy ra:

$\{\begin{array}{c}{\displaystyle \frac{1}{x}=\frac{1}{12}}\\ {\displaystyle \frac{1}{y}=\frac{1}{6}}\end{array}\iff \{\begin{array}{c}x=12\\ y=6\end{array}$

Ta thấy $x=12;y=6$ thỏa mãn điều kiện bài toán.

Vậy người thứ nhất làm một mình trong $12$ ngày thì xong công việc, người thứ hai làm một mình trong $6$ ngày thì xong công việc.

Sử dụng:

- Xem toàn bộ công việc là $1$ (công việc)

- Thực hiện một công việc trong $a$ ngày thì xong việc.

Suy ra trong một ngày thực hiện được ${\displaystyle \frac{1}{a}}$ công việc

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước $1$: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước $2$: Giải hệ phương trình nói trên (sử dụng phương pháp đặt ẩn số phụ).

Bước $3$: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi thời gian một cần cẩu lớn làm một mình xong công việc là $x$ (giờ), thời gian một cần cẩu bé làm một mình xong công việc là $y$ (giờ)

Điều kiện: $x>0;y>0$

Trong $1$ giờ một cần cẩu lớn làm được ${\displaystyle \frac{1}{x}}$ (công việc)

Trong $1$ giờ một cần cẩu bé làm được ${\displaystyle \frac{1}{y}}$ (công việc)

Hai cần cẩu lớn làm trong $6$ giờ và $5$ cần cẩu bé làm trong $3$ giờ thì xong công việc nên ta có:

${\displaystyle \mathrm{6.2.}\frac{1}{x}+\mathrm{5.3.}\frac{1}{y}=1}$$\iff {\displaystyle \frac{12}{x}+\frac{15}{y}=1}$

Nếu cả bảy cần cẩu cùng làm việc từ đầu thì trong $4$ giờ xong việc. Do đó trong $1$ giờ cả $7$ cần cẩu làm được $1:4={\displaystyle \frac{1}{4}}$ công việc, khi đó ta có phương trình:

${\displaystyle \frac{2}{x}+\frac{5}{y}=\frac{1}{4}}$

Ta có hệ phương trình:

$\{\begin{array}{c}{\displaystyle \frac{12}{x}+\frac{15}{y}=1}\\ {\displaystyle \frac{2}{x}+\frac{5}{y}=\frac{1}{4}}\end{array}$

Đặt ${\displaystyle \frac{1}{x}=a;\frac{1}{y}=b}$ $(a>0;b>0)$

Khi đó hệ phương trình trên trở thành:

$\begin{array}{rl}& \{\begin{array}{c}12a+15b=1\\ 2a+5b={\displaystyle \frac{1}{4}}\end{array}\\ & \iff \{\begin{array}{c}12a+15b=1\\ 12a+30b={\displaystyle \frac{3}{2}}\end{array}\\ & \iff \{\begin{array}{c}15b={\displaystyle \frac{1}{2}}\\ 2a+5b={\displaystyle \frac{1}{4}}\end{array}\\ & \iff \{\begin{array}{c}b={\displaystyle \frac{1}{30}}\\ 2a+{\displaystyle 5.\frac{1}{30}=\frac{1}{4}}\end{array}\\ & \iff \{\begin{array}{c}b={\displaystyle \frac{1}{30}}\\ a={\displaystyle \frac{1}{24}}\end{array}\text{(thỏa mãn)}\end{array}$

Suy ra:  

$\{\begin{array}{c}{\displaystyle \frac{1}{x}=\frac{1}{24}}\\ {\displaystyle \frac{1}{y}=\frac{1}{30}}\end{array}\iff \{\begin{array}{c}x=24\\ y=30\end{array}\text{(thỏa mãn)}$

Vậy một cần cẩu lớn làm một mình trong $24$ giờ thì xong công việc, một cần cẩu nhỏ làm một mình trong $30$ giờ thì xong công việc.

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước $1$: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước $2$: Giải hệ phương trình nói trên.

Bước $3$: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

- Công thức tính quãng đường đi được: $S=v.t;$

Trong đó $S$ là quãng đường đi được $(km)$; $v$ là vận tốc $(km/h)$; $t$ là thời gian $(h)$.

Lời giải:

Gọi vận tốc của bác Toàn là $x(km/h)$, vận tốc của cô Ba Ngần  là $y(km/h)$

Điều kiện: $x>0;y>0$

Đổi $1h{30}^{\prime }=1,5h,1h{15}^{\prime }={\displaystyle \frac{5}{4}}h$

Theo đề bài bác Toàn đi được $1$ giờ $30$ phút, cô Ba Ngần đi được $2$ giờ thì gặp nhau. Mà hai người đi ngược chiều nhau nên tổng quãng đường hai người đi được là $38km$, ta có phương trình: $1,5x+2y=38$

Quãng đường bác Toàn đi trong $1$ giờ $15$ phút hay ${\displaystyle \frac{5}{4}}$ giờ là ${\displaystyle \frac{5}{4}x(km)}$

Quãng đường cô Ba Ngần đi trong $1$ giờ $15$ phút hay ${\displaystyle \frac{5}{4}}$ giờ là ${\displaystyle \frac{5}{4}y(km)}$ 

Sau $1$ giờ $15$ phút, hai người còn cách nhau $10,5km$ nên tổng quãng đường hai người đi được là $38-10,5=27,5$ km, ta có phương trình:

${\displaystyle \frac{5}{4}x+\frac{5}{4}y=27,5}$

Ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}1,5x+2y=38\\ {\displaystyle \frac{5}{4}x+\frac{5}{4}y=27,5}\end{array}\\ & \iff \{\begin{array}{c}3x+4y=76\\ 5x+5y=110\end{array}\\ & \iff \{\begin{array}{c}15x+20y=380\\ 15x+15y=330\end{array}\\ & \iff \{\begin{array}{c}5y=50\\ 5x+5y=110\end{array}\\ & \iff \{\begin{array}{c}y=10\\ 5x+5.10=110\end{array}\\ & \iff \{\begin{array}{c}y=10\\ x=12\end{array}\text{(thỏa mãn)}\end{array}$

Vậy vận tốc của bác Toàn là $12km/h$, vận tốc của cô Ba Ngần đi $10km/h.$

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước $1$: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước $2$: Giải hệ phương trình nói trên.

Bước $3$: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

- Công thức tính quãng đường đi được: $S=v.t;$

Trong đó $S$ là quãng đường đi được $(km)$; $v$ là vận tốc $(km/h)$; $t$ là thời gian $(h)$.

- Hai xe đi ngược chiều nhau từ A và B thì tổng quãng đường hai xe đi được cho đến khi gặp nhau bằng khoảng cách AB

- Hai xe khởi hành đồng thời từ A và B đi cùng chiều. Đến khi gặp nhau, hiệu quãng đường hai xe đi được là độ dài AB

Lời giải:

Gọi vận tốc của xe khách là $x(km/h)$, vận tốc của xe hàng là $y(km/h)$

Điều kiện: $x>y>0.$

Đổi $24$ phút $={\displaystyle \frac{2}{5}}$ giờ

Sau khi xe khách đi được $24$ phút $={\displaystyle \frac{2}{5}}$ giờ, xe hàng đi được $36+24=60$ phút = $1$ giờ thì xe khách gặp xe hàng mà hai xe đi ngược chiều nhau nên tổng quãng đường hai xe đi được bằng khoảng cách giữa ga Sài Gòn và ga Dầu Giây, ta có phương trình:

 ${\displaystyle \frac{2}{5}x+y=65}$

Hai xe khởi hành đồng thời và cùng đi Hà Nội thì sau $13$ giờ gặp nhau nên đến khi gặp nhau, xe khách đã đi quãng đường nhiều hơn quãng đường của xe hàng là $65km$, do đó ta có phương trình:

$13x-13y=65$

Ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}{\displaystyle \frac{2}{5}x+y=65}\\ 13x-13y=65\end{array}\\ & \iff \{\begin{array}{c}2x+5y=325\\ x-y=5\end{array}\\ & \iff \{\begin{array}{c}2x+5y=325\\ 2x-2y=10\end{array}\\ & \iff \{\begin{array}{c}7y=315\\ x-y=5\end{array}\\ & \iff \{\begin{array}{c}y=45\\ x-45=5\end{array}\\ & \iff \{\begin{array}{c}y=45\\ x=50\end{array}\end{array}$

Ta thấy $x=50;y=45$ thỏa mãn điều kiện bài toán.

Vậy vận tốc của xe khách là $50km/h$, vận tốc của xe hàng là $45km/h.$

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước $1$: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước $2$: Giải hệ phương trình nói trên.

Bước $3$: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi số thợ cần thiết để làm xong việc là $x$ (người), thời gian cần thiết để làm xong việc là $y$ (ngày)

Điều kiện: $x\in {\mathbb{N}}^{\ast },y>0$

Số ngày công để hoàn thành công việc là $xy$ (ngày)

Nếu giảm $3$ người thì thời gian tăng thêm $6$ ngày, ta có phương trình:

$\left(x-3\right)\left(y+6\right)=xy$

Nếu tăng $2$ người thì thời gian làm giảm $2$ ngày, ta có phương trình:

$\left(x+2\right)\left(y-2\right)=xy$

Ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}\left(x-3\right)\left(y+6\right)=xy\\ \left(x+2\right)\left(y-2\right)=xy\end{array}\\ & \iff \{\begin{array}{c}xy+6x-3y-18=xy\\ xy-2x+2y-4=xy\end{array}\\ & \iff \{\begin{array}{c}2x-y=6\\ -x+y=2\end{array}\iff \{\begin{array}{c}x=8\\ -x+y=2\end{array}\\ & \iff \{\begin{array}{c}x=8\\ y=10\end{array}\end{array}$

Ta thấy $x=8;y=10$ thỏa mãn điều kiện bài toán.

Vậy theo quy định cần có $8$ người thợ và làm trong $10$ ngày.

Đặt $EB=2x(cm)$. Tính $x$ và $y$ để diện tích của hình chữ nhật bằng diện tích hình vuông và ngũ giác $ABCFG$ có chu vi bằng $100+4\sqrt{13}(cm)$

Phương pháp giải:

Sử dụng:

- Diện tích hình chữ nhật bằng tích hai kích thước của nó: $S=a.b$

Trong đó $S$ là diện tích, $a$ là chiều dài, $b$ là chiều rộng của hình chữ nhật.

- Diện tích hình vuông bằng bình phương cạnh của nó: $S=a^2$

- Định lý Pytago: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

- Giải bài toán bằng cách lập hệ phương trình.

Lời giải:

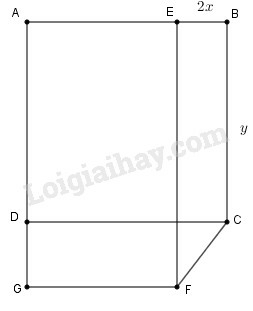
Theo giả thiết ta có: $EB=2x(cm)$ 

Điều kiện: $y>2x>0$

$AE=AB–EB=y–2x(cm)$

$AG=AD+DG$$$\begin{gathered} =y+{\displaystyle \frac{3}{2}EB} \\ =y+{\displaystyle \frac{3}{2}.2x=y+3x(cm)} \end{gathered}$$

Diện tích hình chữ nhật $GAEF$ bằng diện tích hình vuông  $ABCD$ nên ta có phương trình:

$\left(y-2x\right)\left(y+3x\right)=y^2$

Mặt khác theo định lí Pitago ta có:

$$\begin{gathered} FC=\sqrt{E{B}^2+D{G}^2} \\ =\sqrt{4x^2+9x^2}=x\sqrt{13}(cm) \end{gathered}$$

Chu vi của ngũ giác $ABCFG$ bằng: 

$\begin{array}{rl}& AB+BC+CF+FG+GA\\ & =y+y+x\sqrt{13}+y-2x+3x+y\\ & =x\left(1+\sqrt{13}\right)+4y\end{array}$

Chu vi ngũ giác $ABCFG$ bằng $100+4\sqrt{13}(cm)$ nên ta có phương trình:

$x\left(1+\sqrt{13}\right)+4y=100+4\sqrt{13}$

Ta có hệ phương trình:

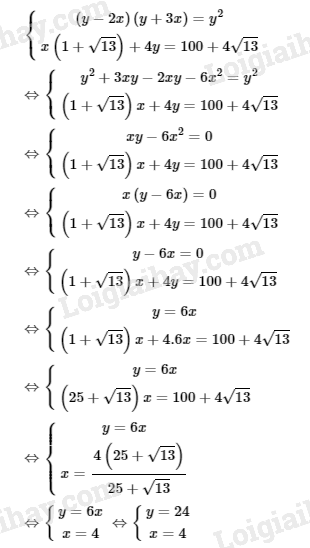
Giá trị $x=4$ và $y=24$ thỏa mãn điều kiện bài toán.

Vậy $x=4(cm);y=24(cm).$

Bài tập bổ sung (trang 15 SBT Toán 9)

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải:

Gọi tuổi của tôi hiện nay là $x$ (tuổi), điều kiện: $x\in {\mathbb{N}}^{\ast }$

Tổng số tuổi của tôi và của em tôi năm nay bằng $26$ nên tuổi của em tôi hiện nay là $26–x$ (tuổi)

Giả sử số năm phải thêm là $y$ (năm) (điều kiện: $y\in {\mathbb{N}}^{\ast })$ để tổng số tuổi của chúng tôi bằng 5 lần tuổi của tôi hiện nay.

Vì sau $y$ năm tổng số tuổi của chúng tôi gấp $5$ lần tuổi của tôi hiện nay nên ta có phương trình:

$\left(x+y\right)+\left(26-x+y\right)=5x$

Tuổi của tôi sau $y$ năm gấp $3$ lần tuổi của em tôi hiện nay nên ta có phương trình:

$x+y=3\left(26-x\right)$

Khi đó ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}\left(x+y\right)+\left(26-x+y\right)=5x\\ x+y=3\left(26-x\right)\end{array}\\ & \iff \{\begin{array}{c}5x-2y=26\\ 4x+y=78\end{array}\\ & \iff \{\begin{array}{c}5x-2y=26\\ 8x+2y=156\end{array}\\ & \iff \{\begin{array}{c}13x=182\\ 4x+y=78\end{array}\\ & \iff \{\begin{array}{c}x=14\\ 4.14+y=78\end{array}\\ & \iff \{\begin{array}{c}x=14\\ y=22\end{array}\end{array}$

Ta thấy $x=14;y=22$ thỏa mãn điều kiện bài toán.

Vậy hiện nay tuổi của tôi là $14$ tuổi, tuổi của em tôi là $26–14=12$ (tuổi).

Phương pháp giải:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước $1$: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước $2$: Giải hệ phương trình nói trên.

Bước $3$: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

- Công thức tính quãng đường đi được: $S=v.t;$

Trong đó $S$ là quãng đường đi được $(km)$; $v$ là vận tốc $(km/h)$; $t$ là thời gian $(h)$.

Lời giải:

Gọi vận tốc người đi xe đạp là $y$ (km/phút), vận tốc xe khách là $z$ (km/phút)

Điều kiện: $z>y>0$

- Xét trường hợp các xe khách đi cùng chiều với người đi xe đạp.

Giả sử khi xe khách thứ nhất vượt người đi xe đạp tại điểm $B$ thì xe khách thứ hai ở điểm $A$ như hình vẽ.

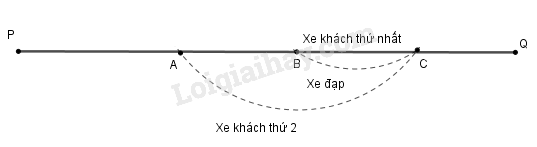
Hai xe khách khởi hành cách nhau $x$ phút nên quãng đường $AB$ là quãng đường mà xe khách phải đi trong $x$ phút và $AB=xz$ (km).

Gọi điểm mà xe khách thứ hai vượt người đi xe đạp là $C$ thì quãng đường $BC$ là quãng đường người đi xe đạp đi trong $15$ phút nên $BC=15y$ (km). Quãng đường $AC$ là quãng đường xe khách đi trong $15$ phút nên $AC=15z$ (km).

Ta có phương trình: $xz+15y=15z$

- Xét trường hợp các xe khách đi ngược chiều với người đi xe đạp.

Giả sử người đi xe đạp gặp xe khách thứ nhất đi ngược chiều tại điểm $D$ thì xe khách thứ hai đi ngược chiều  đang ở vị trí $E$ như hình vẽ.

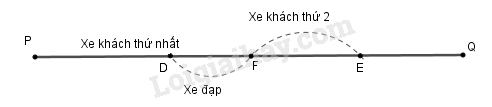
Hai xe khách khởi hành cách nhau $x$ phút nên $DE=xz$ (km). Sau đó $10$ phút, người đi xe đạp gặp xe khách thứ hai tại điểm $F$. Khi đó, quãng đường $DF$ là quãng đường người đi xe đạp đi trong $10$ phút nên $DF=10y$ (km). Quãng đường $EF$ là quãng đường xe khách đi trong $10$ phút nên $EF=10z$ (km).

Ta có phương trình:  $10y+10z=xz$

Ta có hệ phương trình:

$\begin{array}{rl}& \{\begin{array}{c}xz+15y=15z\\ 10y+10z=xz\end{array}\\ & \iff \{\begin{array}{c}xz+15y=15z\\ xz-10y=10z\end{array}\\ & \iff \{\begin{array}{c}x+{\displaystyle 15.\frac{y}{z}=15}\\ x-{\displaystyle 10.\frac{y}{z}=10}\end{array}\end{array}$

Đặt ${\displaystyle \frac{y}{z}=t}$ $(t>0)$

Khi đó hệ phương trình trên trở thành:

$\begin{array}{rl}& \{\begin{array}{c}x+15t=15\\ x-10t=10\end{array}\iff \{\begin{array}{c}25t=5\\ x-10t=10\end{array}\\ & \iff \{\begin{array}{c}t={\displaystyle \frac{1}{5}}\text{(thoả mãn)}\\ x-10t=10\end{array}\\ & \iff \{\begin{array}{c}t={\displaystyle \frac{1}{5}}\\ x-10.{\displaystyle \frac{1}{5}=10}\end{array}\\ & \iff \{\begin{array}{c}t={\displaystyle \frac{1}{5}}\\ x=12\end{array}\end{array}$

Suy ra: $x=12;{\displaystyle \frac{y}{z}=\frac{1}{5}\Rightarrow 5y=z}$

Vậy cứ $12$ phút lại có một chuyến xe khách rời bến và vận tốc của xe khách gấp $5$ lần vận tốc của người đi xe đạp.