Với Giải toán 10 trang 47 Tập 1 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải toán 10 trang 47 Tập 1 Chân trời sáng tạo
Thực hành 4 trang 47 Toán lớp 10: a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
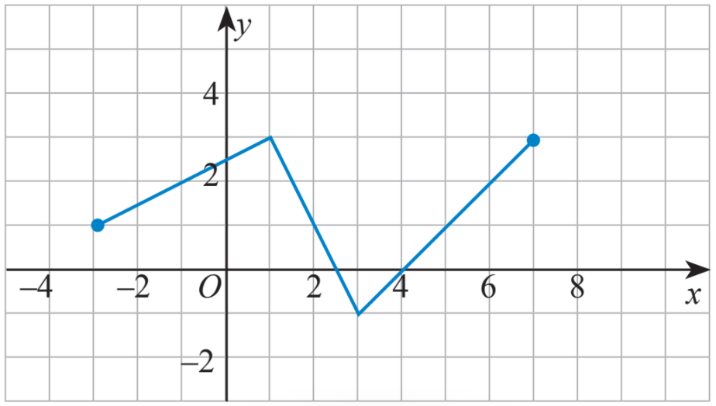
b) Xét tính đồng biến, nghịch biến của hàm số trên khoảng (2; 5).
Phương pháp giải:
a) Quan sát đồ thị trên các khoảng (-3; 1), (1;3), (3;7)
Khi hàm số đồng biến trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải.
Khi hàm số nghịch biến trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.
b)
Bước 1: Lấy là hai số tùy ý sao cho .
Bước 2: So sánh và
Bước 3: Kết luận tính đồng biến, nghịch biến
+ Nếu thì hàm số đồng biến trên khoảng (2; 5)
+ Nếu thì hàm số nghịch biến trên khoảng (2; 5)
Lời giải:
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thì có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thì có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thì có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số trên khoảng (2; 5).
Lấy là hai số tùy ý sao cho .
Do và nên , suy ra hay
Từ đây suy ra
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).
Bài 1 trang 47 Toán lớp 10: Tìm tập xác định của các hàm số sau:
a) f(x) =
b)
Phương pháp giải:
Tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức có nghĩa.
a) có nghĩa
b) có nghĩa
Lời giải:
a) Biểu thức có nghĩa khi và chỉ khi tức là khi
Vậy tập xác định của hàm số này là
b) Biểu thức có nghĩa khi và chỉ khi tức là khi
Vậy tập xác định của hàm số này là
Bài 2 trang 47 Toán lớp 10: Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10.
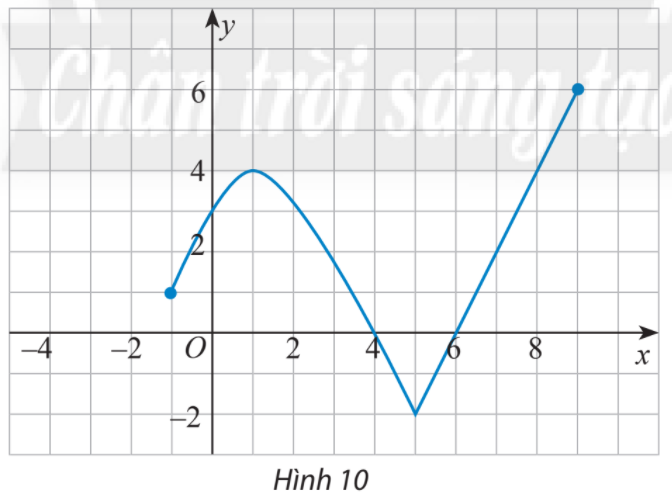
Phương pháp giải:
+) Tập xác định là tập hợp các giá trị của biến số x.
+) Tập giá trị là tập hợp các giá trị y (tương ứng với x thuộc tập xác định)
Lời giải:
Từ đồ thị, ta có:
Đồ thị hàm số xác định (liền mạch) từ đến , do đó tập xác định của hàm số là
Tập giá trị , vậy
Bài 3 trang 47 Toán lớp 10: Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
a)
b)
Phương pháp giải:
Bước 1: Lấy là hai số tùy ý sao cho .
Bước 2: Tìm điều kiện để và
a)
b)
Bước 3: Kết luận khoảng đồng biến, nghịch biến
+ với thì hàm số đồng biến trên khoảng
+ với thì hàm số nghịch biến trên khoảng
Lời giải:
a) Xét hàm số xác định trên
Lấy là hai số tùy ý sao cho .
Do nên , suy ra
Từ đây ta có
Vậy hàm số ngịch biến (giảm) trên
b) Xét hàm số xác định trên
+ Trên khoảng lấy là hai số tùy ý sao cho ., ta có:
Do nên và do nên .
Từ đây suy ra hay
Vậy hàm số nghịch biến (giảm) trên khoảng
+ Trên khoảng lấy là hai số tùy ý sao cho ., ta có:
Do nên và do nên .
Từ đây suy ra hay
Vậy hàm số đồng biến (tăng) trên khoảng
Bài 4 trang 47 Toán lớp 10: Vẽ đồ thị hàm số biết rằng hàm số này còn được viết như sau:
Phương pháp giải:
Vẽ đồ thị từng hàm trên mỗi khoảng cho trước
Lời giải:
Hàm số xác định trên
Trên khoảng ta vẽ đồ thị hàm số , đi qua 2 điểm
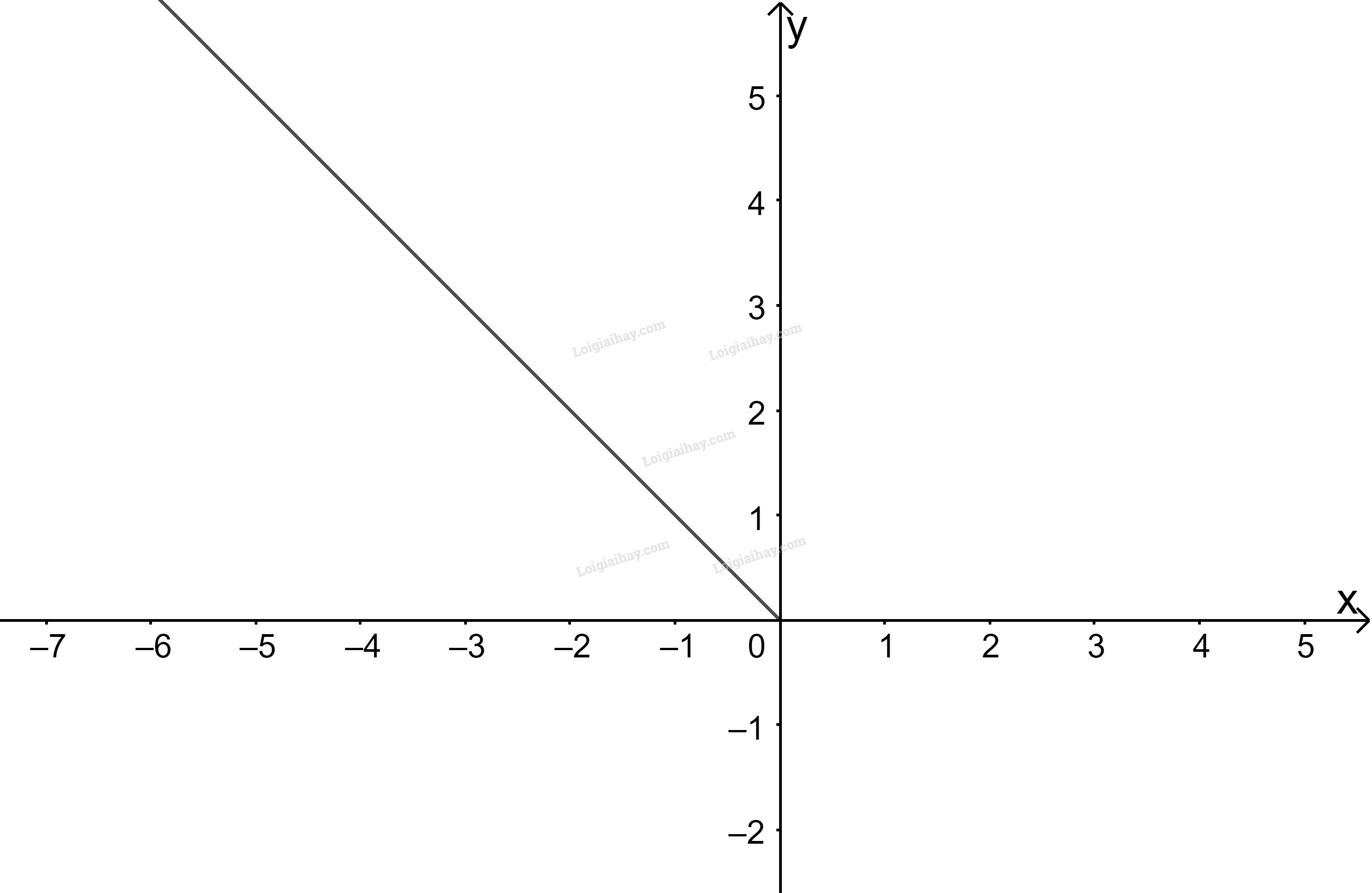
Trên khoảng ta vẽ đồ thị hàm số , đi qua 2 điểm
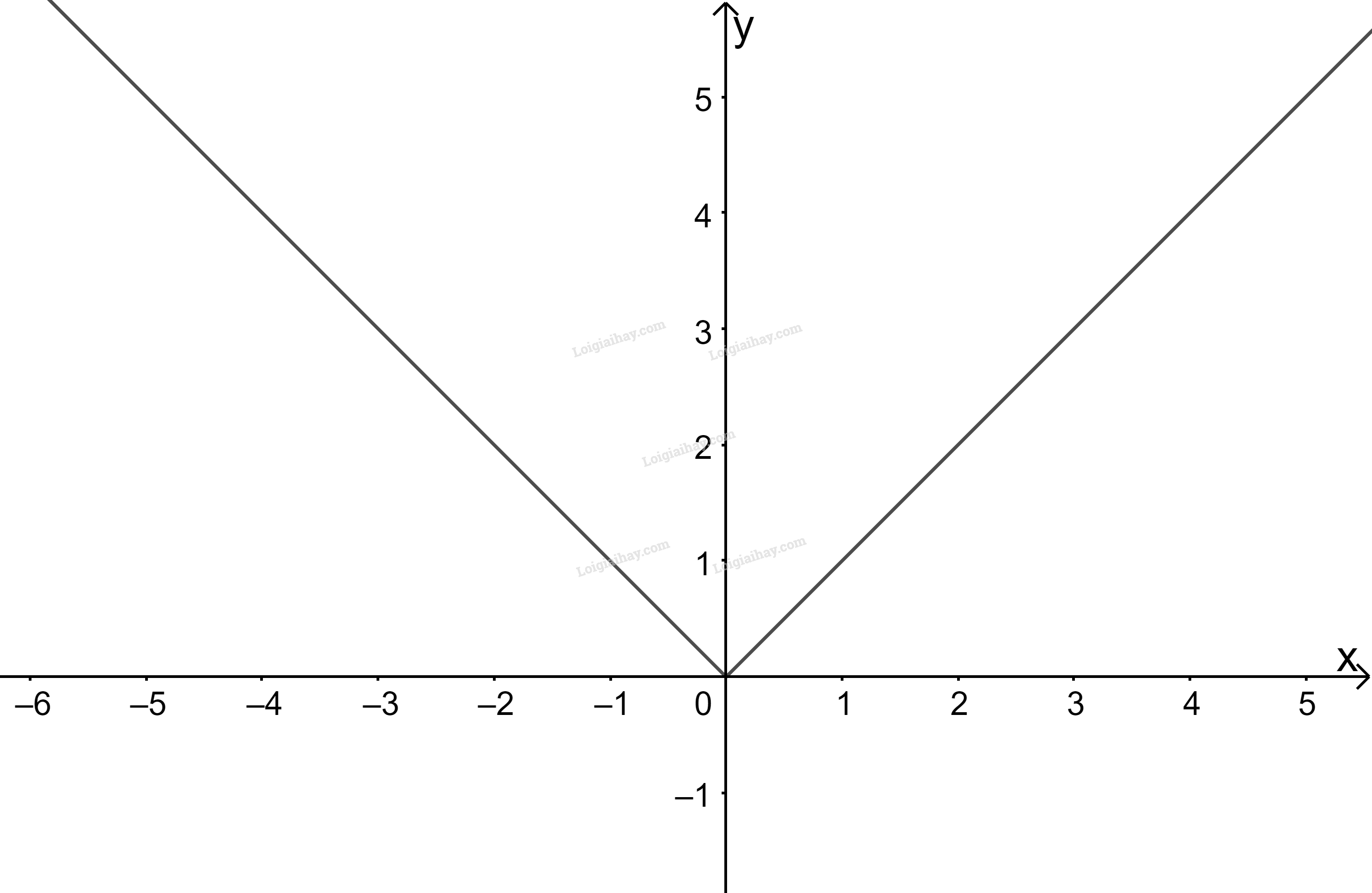
Như vậy ta được đồ thị hàm số .
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Giải toán lớp 10 trang 41 Tập 1
Giải toán lớp 10 trang 43 Tập 1
Giải toán lớp 10 trang 44 Tập 1
Giải toán lớp 10 trang 45 Tập 1
Giải toán lớp 10 trang 48 Tập 1