SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây

SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9

thuy an pham Ngày: 19-05-2022 Lớp 9

1.6 K

Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây

Bài 24 trang 160 SBT Toán 9 tập 1: Cho hình

74,

trong đó

M N = P Q .

Chứng minh rằng:

$a)$ $A E = A F$

$b)$ $A N = A Q .$

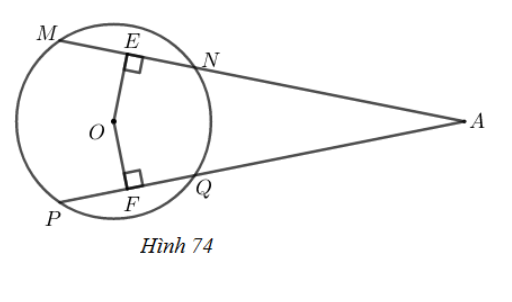
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 1)

Phương pháp giải:

Sử dụng kiến thức: Trong một đường tròn:

+) Hai dây bằng nhau thì cách đều tâm.

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Lời giải:

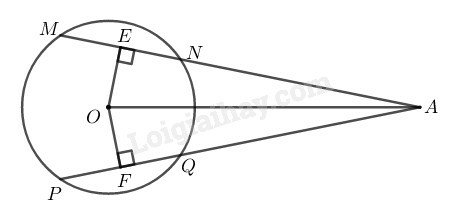
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 2)

$a)$ Nối $O A$

Ta có: $M N = P Q (g t)$

Suy ra: $O E = O F$ (hai dây bằng nhau cách đều tâm)

Xét hai tam giác $O A E$ và $O A F,$ ta có:

+) $\hat{O E A} = \hat{O F A} = 90^{\circ}$

+) $O A$ chung

+) $O E = O F$ ( chứng minh trên)

Suy ra: $∆ O A E = ∆ O A F$ (cạnh huyền, cạnh góc vuông)

Suy ra: $A E = A F$

$b)$ Xét (O) có: $O E ⊥ M N (g t)$

Suy ra: $E N = \frac{1}{2} M N$ (đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy) $(1)$

Xét (O) có: $O F ⊥ P Q (g t)$

Suy ra: $F Q = \frac{1}{2} P Q$ (đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy) $(2)$

Mặt khác: $M N = P Q (g t) (3)$

Từ $(1),$ $(2)$ và $(3)$ suy ra: $E N = F Q (4)$

Mà $A E = A F$ ( chứng minh câu a)

Hay $A N + N E = A Q + Q F (5)$

Từ $(4)$ và $(5)$ suy ra: $A N = A Q .$

Bài 25 trang 160 SBT Toán 9 tập 1: Cho hình

75,

trong đó hai dây

C D, E F

bằng nhau và vuông góc với nhau tại

I,

I C = 2 c m,

I D = 14 c m .

Tính khoảng cách từ

O

đến mỗi dây.

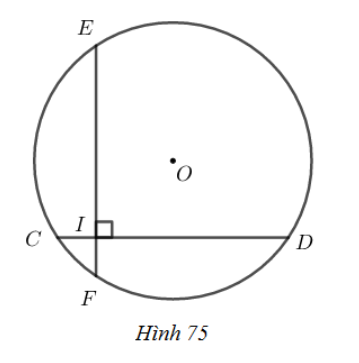
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 3)

Phương pháp giải:

Sử dụng kiến thức: Trong một đường tròn:

+) Hai dây bằng nhau thì cách đều tâm.

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Lời giải:

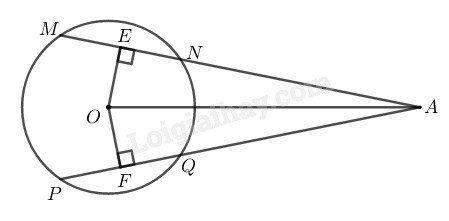
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 4)

Kẻ $O H ⊥ C D,$ $O K ⊥ E F$

Vì tứ giác $O K I H$ có ba góc vuông nên nó là hình chữ nhật.

Ta có: $C D = E F (g t)$

Suy ra: $O H = O K$ (hai dây bằng nhau cách đều tâm)

Suy ra tứ giác $O K I H$ là hình vuông.

Ta có: $C D = C I + I D = 2 + 14 = 16 (c m)$

Xét (O) có $O H ⊥ C D$ mà OH là 1 phần đường kính và CD là dây cung nên $H C = H D = \frac{C D}{2} = 8$ $(c m)$ (quan hệ giữa đường kính và dây cung)

Suy ra $I H = H C - C I = 8 - 2 = 6 (c m)$

Do đó $O H = O K = I H = 6 (c m)$ (do $O K I H$ là hình vuông).

Vậy khoảng cách từ $O$ đến mỗi dây là 6cm.

Bài 26 trang 160 SBT Toán 9 tập 1: Cho đường tròn

(O),

dây

A B

và dây

C D,

A B < C D .

Giao điểm

K

của các đường thẳng

A B,

C D

nằm ngoài đường tròn. Đường tròn

(O; O K)

cắt

K A

và

K C

tại

M

và

N .

Chứng minh rằng

K M < K N .

Phương pháp giải:

Sử dụng kiến thức: Trong hai dây của một đường tròn:

+) Dây nào lớn hơn thì dây đó gần tâm hơn.

+) Dây nào gần tâm hơn thì dây đó lớn hơn.

Lời giải:

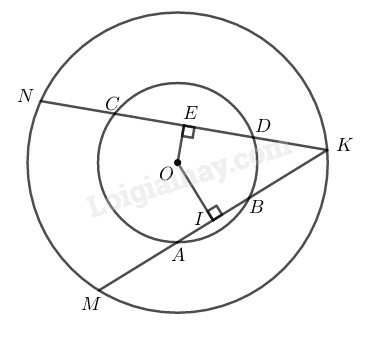
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 5)

Kẻ $O I ⊥ A B,$ $O E ⊥ C D$

Trong $(O; O A)$ ta có: $A B < C D (g t)$

Suy ra: $O I > O E$ (dây lớn hơn gần tâm hơn)

Trong $(O; O K)$ ta có: $O I > O E$ (cmt)

Suy ra: $K M < K N$ (dây gần tâm hơn thì lớn hơn).

Bài 27 trang 160 SBT Toán 9 tập 1: Cho đường tròn

(O)

và điểm

I

nằm bên trong đường tròn. Chứng minh rằng dây

A B

vuông góc với

O I

tại

I

ngắn hơn mọi dây khác đi qua

I .

Phương pháp giải:

Sử dụng kiến thức: Trong hai dây của một đường tròn:

+) Dây nào lớn hơn thì dây đó gần tâm hơn.

Lời giải:

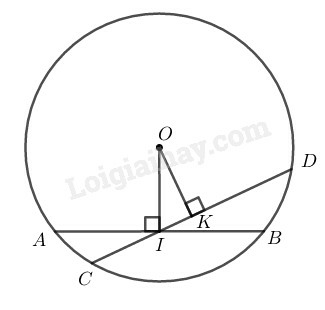
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 6)

Gọi $C D$ là dây bất kì đi qua $I$ và $C D$ không vuông góc với $O I .$

Kẻ $O K ⊥ C D$

Tam giác $O K I$ vuông tại $K$ nên $O I > O K$

Suy ra: $A B < C D$ ( dây lớn hơn gần tâm hơn)

Vậy dây $A B$ vuông góc với $I O$ tại $I$ ngắn hơn mọi dây khác đi qua $I .$

Bài 28 trang 160 SBT Toán 9 tập 1: Tam giác

A B C

nội tiếp đường tròn

(O)

có

\hat{A} > \hat{B} > \hat{C} .

Gọi

O H, O I, O K

theo thứ tự là khoảng cách từ

O

đến

B C,

A C,

A B .

So sánh các độ dài

O H, O I, O K .

Phương pháp giải:

Sử dụng kiến thức:

+) Trong một tam giác, cạnh nào đối diện với góc lớn hơn thì cạnh đó lớn hơn.

+) Trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.

Lời giải:

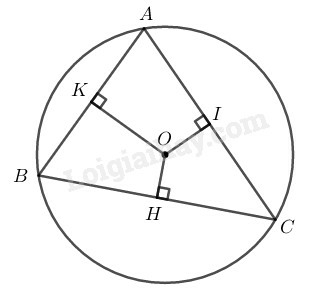
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 7)

Tam giác $A B C$ có $\hat{A} > \hat{B} > \hat{C}$ nên suy ra:

$B C > A C > A B$ (cạnh đối diện góc lớn hơn thì lớn hơn)

Ta có $A B,$ $B C,$ $A C$ lần lượt là các dây cung của đường tròn $(O)$

Mà $B C > A C > A B$ nên suy ra:

$O H < O I < O K$ ( dây lớn hơn thì gần tâm hơn).

Bài 29 trang 161 SBT Toán 9 tập 1: Cho đường tròn

(O),

hai dây

A B, C D

bằng nhau và cắt nhau tại điểm

I

nằm bên trong đường tròn. Chứng minh rằng:

$a)$ $I O$ là tia phân giác của một trong hai góc tạo bởi hai dây $A B$ và $C D .$

$b)$ Điểm $I$ chia $A B,$ $C D$ thành các đoạn thẳng bằng nhau đôi một.

Phương pháp giải:

Sử dụng kiến thức: Trong một đường tròn:

+) Hai dây bằng nhau thì cách đều tâm.

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Lời giải:

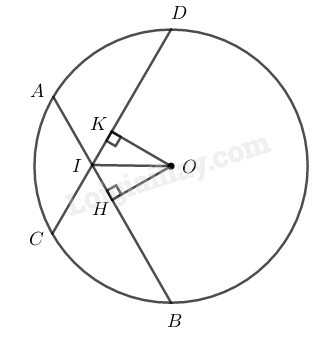
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 8)

$a)$ Kẻ $O H ⊥ A B,$ $O K ⊥ C D$

Ta có: $A B = C D (g t)$

Suy ra: $O H = O K$ (hai dây bằng nhau cách đều tâm)

Do đó O nằm trên tia phân giác của góc BID (tính chất đường phân giác)

Vậy $I O$ là tia phân giác của góc $B I D$

$b)$ Xét hai tam giác $O I H$ và $O I K,$ ta có:

+) $\hat{O H I} = \hat{O K I} = 90^{\circ}$

+) $O I$ chung

+) $O H = O K$ (chứng minh trên)

Suy ra: $∆ O I H = ∆ O I K$ (cạnh huyền, cạnh góc vuông)

Suy ra: $I H = I K (1)$

Xét (O) có $O H ⊥ A B$ nên $H A = H B = \frac{1}{2} A B$ (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Xét (O) có $O K ⊥ D C$ nên $K C = K D = \frac{1}{2} C D$ (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Mà $A B = C D$ (gt) nên $H A = K C$ hay $A I + I H = I C + I K$ mà $I H = I K$ (theo (1))

Suy ra: $I A = I C$

Ta lại có $A B = C D$ (gt) hay $I A + I B = I C + I D$ mà $I A = I C$ (cmt) nên $I B = I D .$

Vậy $I A = I C, I B = I D$ .

Bài 30 trang 161 SBT Toán 9 tập 1: Cho đường tròn tâm

O

bán kính

25 c m .

Hai dây

A B, C D

song song với nhau và có độ dài theo thứ tự bằng

40 c m,

48 c m .

Tính khoảng cách giữa hai dây ấy.

Phương pháp giải:

Sử dụng kiến thức:

+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+) Sử dụng định lí Py-ta-go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Lời giải:

Kẻ $O K ⊥ C D,$ $O H ⊥ A B .$

Xét (O) có $O K ⊥ C D$ mà OK là 1 phần đường kính và CD là dây cung $\Rightarrow C K = D K = \frac{1}{2} C D$ (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Xét (O) có $O H ⊥ A B$ mà OH là 1 phần đường kính và CD là dây cung $\Rightarrow A H = B H = \frac{1}{2} A B$ (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Vì $A B / / C D$ nên $H, O, K$ thẳng hàng.

Áp dụng định lí Pi-ta-go vào tam giác vuông $O B H,$ ta có:

$O B^{2} = B H^{2} + O H^{2}$

Suy ra: $O H^{2} = O B^{2} - B H^{2}$ $= 25^{2} - 20^{2} = 225$

$\Rightarrow O H = 15 (c m)$

Áp dụng định lí Pi-ta-go vào tam giác vuông $O D K,$ ta có:

$O D^{2} = D K^{2} + O D^{2}$

Suy ra: $O K^{2} = O D^{2} - D K^{2}$ $= 25^{2} - 24^{2} = 49$

$\Rightarrow O K = 7 (c m)$

* Trường hợp $O$ nằm giữa hai dây $A B$ và $C D$ :

$H K = O H + O K = 15 + 7 = 22 (c m)$

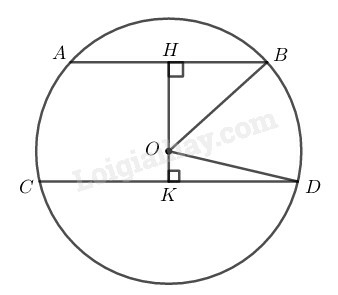
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 9)

* Trường hợp $O$ nằm ngoài hai dây $A B$ và $C D$ :

$H K = O H - O K = 15 - 7 = 8 (c m) .$

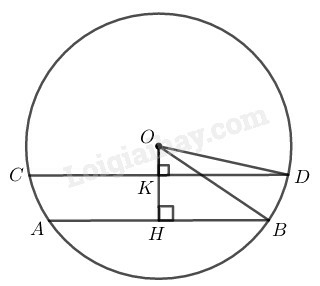
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 10)

Bài 31 trang 161 SBT Toán 9 tập 1: Cho đường tròn

(O),

các bán kính

O A

và

O B .

Trên cung nhỏ

A B

lấy các điểm

M

và

N

sao cho

A M = B N .

Gọi

C

là giao điểm của các đường thẳng

A M

và

B N .

Chứng minh rằng:

$a)$ $O C$ là tia phân giác của góc $A O B .$

$b)$ $O C$ vuông góc với $A B .$

Phương pháp giải:

Sử dụng kiến thức:

+) Trong một đường tròn: Hai dây bằng nhau thì cách đều tâm.

+) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy vừa là đường cao, đường phân giác.

Lời giải:

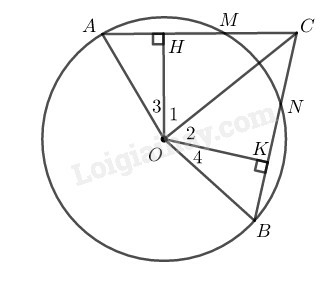
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 11)

$a)$ Kẻ $O H ⊥ A M, O K ⊥ B N$

Ta có: $A M = B N (g t)$

Suy ra: $O H = O K$ (hai dây bằng nhau cách đều tâm)

Xét hai tam giác $O C H$ và $O C K,$ ta có:

$\hat{O H C} = \hat{O K C} = 90^{\circ}$

$O C$ chung

$O H = O K$ (chứng minh trên)

Suy ra: $∆ O C H = ∆ O C K$ (cạnh huyền, cạnh góc vuông)

$\hat{O_{1}} = \hat{O_{2}}$ (1)

Xét hai tam giác $O A H$ và $O B K,$ ta có:

$\hat{O H A} = \hat{O K B} = 90^{\circ}$

$O A = O B$ (cùng bằng bán kính)

$O H = O K$ ( chứng minh trên)

Suy ra: $∆ O A H = ∆ O B K$ (cạnh huyền, cạnh góc vuông)

$\hat{O_{3}} = \hat{O_{4}}$ (2)

Từ (1) và (2) suy ra: $\hat{O_{1}} + \hat{O_{3}} = \hat{O_{2}} + \hat{O_{4}}$ hay $\hat{A O C} = \hat{B O C}$

Vậy $O C$ là tia phân giác của $\hat{A O B}$

$b)$ Tam giác $O A B$ cân tại $O$ (do $O A = O B)$ có $O C$ là tia phân giác nên $O C$ đồng thời cũng là đường cao ( tính chất tam giác cân).

Suy ra: $O C ⊥ A B .$

Chú ý: TH hình vẽ dưới đây các em vẫn làm như trên:

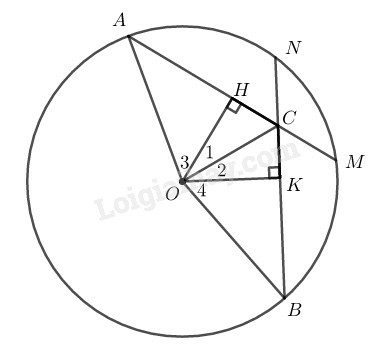
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 12)

Bài 32* trang 161 SBT Toán 9 tập 1: Cho đường tròn tâm

O

bán kính

5 d m,

điểm

M

cách

O

là

3 d m .

$a)$ Tính độ dài dây ngắn nhất đi qua điểm $M .$

$b)$ Tính độ dài dây dài nhất đi qua $M .$

Phương pháp giải:

Sử dụng kiến thức:

+) Trong các dây của một đường tròn, dây lớn nhất là đường kính.

+) Trong hai dây của đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.

+) Trong một đường tròn, đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy.

Lời giải:

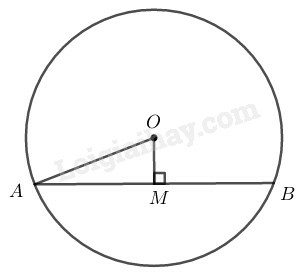
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 13)

$a)$ Dây đi qua $M$ ngắn dây là dây $A B$ vuông góc với $O M$ (xem bài 27 trang 160 SBT toán 9 tập 1)

Áp dụng định lí Pi-ta-go vào tam giác vuông $O A M$ ta có:

$O A^{2} = A M^{2} + O M^{2}$

Suy ra: $A M^{2} = O A^{2} - O M^{2} = 5^{2} - 3^{2} = 16$

$A M = 4 (d m)$

Xét (O) có $O M ⊥ A B$ mà OM là 1 phần đường kính và AB là dây cung

Suy ra M là trung điểm dây AM (đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy), do đó $A M = \frac{1}{2} A B$

Hay: $A B = 2 A M = 2.4 = 8 (d m)$

$b)$ Dây đi qua $M$ lớn nhất khi nó là đường kính của đường tròn $(O) .$ Vậy dây có độ dài bằng $2 R = 2.5 = 10 (d m)$

Bài 33* trang 161 SBT Toán 9 tập 1: Cho đường tròn

(O),

hai dây

A B

và

C D

cắt nhau tại điểm

M

nằm bên trong đường tròn. Gọi

H

và

K

theo thứ tự là trung điểm của

A B

và

C D .

Cho biết

A B > C D,

chứng minh rằng

Phương pháp giải:

Sử dụng kiến thức:

+) Trong hai dây của một đường tròn: Dây nào lớn hơn thì dây đó gần tâm hơn.

+) Trong một đường tròn: Đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó.

+) Định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Lời giải:

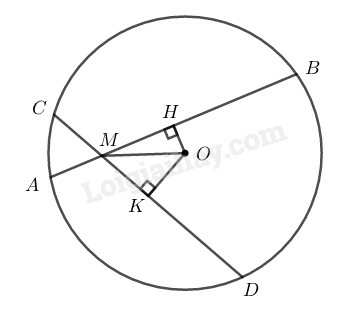
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 14)

Xét (O) có $H A = H B (g t)$

Suy ra: $O H ⊥ A B$ (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)

Xét (O) có $K C = K D (g t)$

Suy ra: $O K ⊥ C D$ (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)

Mà $A B > C D (g t)$

Nên $O K > O H$ ( dây lớn hơn thì gần tâm hơn)

Áp dụng định lí Pi-ta-go vào tam giác vuông $O H M$ ta có:

$O M^{2} = O H^{2} + H M^{2}$

Suy ra: $H M^{2} = O M^{2} - O H^{2}$ $(1)$

Áp dụng định lí Pi-ta-go vào tam giác vuông $O K M,$ ta có:

$O M^{2} = O K^{2} + K M^{2}$

Suy ra: $K M^{2} = O M^{2} - O K^{2}$ $(2)$

Mà $O H < O K (c m t)$ $(3)$

Từ $(1),$ $(2)$ và $(3)$ suy ra: $H M^{2} > K M^{2}$ hay $H M > K M .$

Bài 34* trang 161 SBT Toán 9 tập 1: Cho đường tròn

(O)

và hai điểm

A, B

nằm bên trong đường tròn và không cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao cho điểm

A

nằm trên một dây, điểm

B

nằm trên dây còn lại.

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

+) Sử dụng kiến thức: Trong một đường tròn, hai dây cách đều tâm thì bằng nhau.

Lời giải:

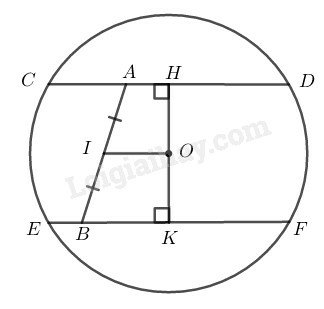
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 15)

* Cách dựng

− Dựng trung điểm $I$ của $A B .$

− Qua $A$ dựng dây $C D$ song song với $O I .$

− Qua $B$ dựng dây $E F$ song song với $O I .$

Ta được $C D$ và $E F$ là hai dây cần dựng.

* Chứng minh

Ta có: $C D / / O I, E F / / O I$

Suy ra: $C D / / E F$

Kẻ $O H ⊥ C D$ cắt $E F$ tại $K$

Suy ra: $O K ⊥ E F$

Xét hình thang AHKB (do AH//BK) có $O I / / A H / / B K$ và I là trung điểm của AB nên O là trung điểm của HK.

Suy ra: $O H = O K$

Vậy $C D = E F$ (hai dây cách đều tâm thì bằng nhau)

* Biện luận

Bài toán có một nghiệm hình.

Bài tập bổ sung (trang 161 SBT Toán 9)

Bài 3.1 trang 161 SBT Toán 9 tập 1: Cho đường tròn

(O)

đường kính

6 c m,

dây

A B

bằng

2 c m .

Khoảng cách từ

O

đến

A B

bằng:

$(A)$ $\sqrt{35} c m$ ; $(B)$ $\sqrt{5} c m$ ;

$(C)$ $4 \sqrt{2} c m$ ; $(D)$ $2 \sqrt{2} c m$ .

Hãy chọn phương án đúng.

Phương pháp giải:

Sử dụng kiến thức:

+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+) Sử dụng định lí Py-ta-go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Lời giải:

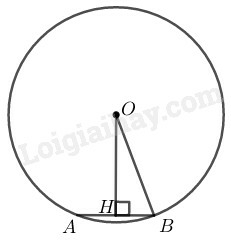
SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 16)

Ta có: $O A = O B = 6 : 2 = 3 c m$

Kẻ $O H ⊥ A B$ tại $H$ mà OH là 1 phần đường kính và AB là dây cung của đường tròn tâm O

$\Rightarrow A H = H B = \frac{1}{2} A B = 1 c m$ (quan hệ giữa đường kính và dây)

Xét trong $Δ O H B,$ có:

$O B^{2} = O H^{2} + H B^{2}$ (định lý Pytago)

$\Rightarrow O H^{2} = O B^{2} - H B^{2}$

$O H^{2} = 3^{2} - 1^{2} = 8$

$\Rightarrow O H = 2 \sqrt{2}$

Vậy chọn $(D) .$

Bài 3.2 trang 161 SBT Toán 9 tập 1: Cho đường tròn

(O),

điểm

I

nằm bên trong đường tròn

(

I

khác

O) .

Dựng dây

A B

đi qua

I

và có độ dài ngắn nhất.

Phương pháp giải:

Sử dụng kiến thức: Trong một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.

Lời giải:

SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 17)

Dây $A B$ phải dựng vuông góc với $O I$ tại $I .$

Bài 3.3* trang 161 SBT Toán 9 tập 1: Cho đường tròn

(O; 25 c m),

điểm

C

cách

O

là

7 c m .

Có bao nhiêu dây đi qua

C

có độ dài là một số nguyên xentimét

?

Phương pháp giải:

Sử dụng kiến thức:

+) Trong các dây của một đường tròn, dây lớn nhất là đường kính.

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Lời giải:

SBT Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây | Giải SBT Toán lớp 9 (ảnh 18)

Dây lớn nhất đi qua $C$ là đường kính $E F = 50 c m .$

Dây nhỏ nhất đi qua $C$ là dây $A B$ vuông góc với $O C$ tại $C,$ $A B = 48 c m .$

$($ Vì tam giác $O A C$ vuông tại $C,$ theo định lý Pytago ta có $A C = \sqrt{O A^{2} - O C^{2}}$ $= \sqrt{25^{2} - 7^{2}} = 24 c m,$ mà $O C ⊥ A B$ tại C nên C là trung điểm AB (quan hệ giữa đường kính và dây cung), suy ra $A B = 2 A C = 2.24 = 48 c m)$

Có hai dây đi qua $C$ có độ dài $49 c m$ $($ là dây $G H$ và $I K$ đối xứng nhau qua $E F$ , hai dây đối xứng qua một đường thẳng thì có độ dài bằng nhau)