Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 2: Phương trình mặt phẳng chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Phương trình mặt phẳng lớp 12.
Giải bài tập Toán lớp 12 Bài 2: Phương trình mặt phẳng
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 70 SGK Hình học 12: Trong không gian
cho ba điểm
. Hãy tìm tọa độ một vecto pháp tuyến của mặt phẳng
.
Phương pháp giải:
- Véc tơ pháp tuyến của mặt phẳng vuông góc với cả hai véc tơ và
- Tính tích có hướng của hai véc tơ và chọn ra một véc tơ pháp tuyến của mặt phẳng.
Lời giải:
Ta có:
Chọn là pháp tuyến của mặt phẳng .
Lưu ý: Các em thể chọn véc tơ pháp tuyến khác , chẳng hạn như hay nhưng để tiện cho tính toán ta thường chọn tọa độ đơn giản nhất
Trả lời câu hỏi 2 trang 72 SGK Hình học 12: Hãy tìm một vecto pháp tuyến của mặt phẳng
.
Phương pháp giải:
Mặt phẳng có một véc tơ pháp tuyến là
Lời giải:
Một vecto pháp tuyến của mặt phẳng là:
Trả lời câu hỏi 3 trang 72 SGK Hình học 12: Lập phương trình tổng quát của mặt phẳng
với
.
Phương pháp giải:
- Tính véc tơ tích có hướng của hai véc tơ và .
- Chọn một véc tơ cùng phương với véc tơ trên làm VTPT của mặt phẳng.
- Viết phương trình
Lời giải:
⇒ Một vecto pháp tuyến của mặt phẳng là
Phương trình tổng quát của mặt phẳng với là:
Hay .
Trả lời câu hỏi 4 trang 73 SGK Hình học 12: Nếu
hoặc
thì mặt phẳng
có đặc điểm gì ?
Lời giải:
mặt phẳng hoặc chứa trục mặt phẳng hoặc chứa trục .
Trả lời câu hỏi 5 trang 74 SGK Hình học 12: Nếu
và
hoặc nếu
và
thì mặt phẳng
có đặc điểm gì?
Lời giải:
và mặt phẳng hoặc trùng với
và mặt phẳng hoặc trùng với
Trả lời câu hỏi 6 trang 74 SGK Hình học 12: Cho hai mặt phẳng
và
có phương trình
; .
Có nhận xét gì về vecto pháp tuyến của chúng?
Phương pháp giải:
Tìm hai VTPT của hai mặt phẳng rồi suy ra nhập xét.
Lời giải:
Ta thấy nên chúng cùng phương.
Trả lời câu hỏi 7 trang 80 SGK Hình học 12: Tính khoảng cách giữa hai mặt phẳng
và
cho bởi các phương trình sau đây:
Phương pháp giải:
- Chứng minh hai mặt phẳng song song.
- Tính khoảng cách giữa hai mặt phẳng ở đó tọa điểm chọn trước thuộc .
- Công thức khoảng cách:
Lời giải:
Ta thấy: và cùng có VTPT .
Dễ thấy điểm nhưng nên .
Từ đó
Vậy khoảng cách giữa hai mặt phẳng bằng .
Câu hỏi và bài tập (trang 80, 81 SGK Hình học 12)
Bài 1 trang 80 SGK Hình học 12: Viết phương trình mặt phẳng:
a) Đi qua điểm và nhận làm vectơ pháp tuyến.
b) Đi qua điểm và song song với giá của các vectơ và .
c) Đi qua ba điểm và .
Phương pháp giải:
a) Phương trình mặt phẳng đi qua và có VTPT có dạng:
b) Mặt phẳng song song với các vecto VTPT của là:
Sau đó áp dụng công thức như câu a để lập phương trình mặt phẳng.
c) Mặt phẳng đi qua điểm và có VTPT:
Khi đó áp dụng công thức như câu a để lập phương trình mặt phẳng.
Lời giải:
a)
Mặt phẳng đi qua điểm và nhận làm vectơ pháp tuyến có phương trình:
.
b)
Gọi là mặt phẳng cần lập. Theo đề bài ta có: song song với
Khi đó ta có VTPT của là:
Do đó ta chọn một VTPT của có tọa độ
Phương trình mặt phẳng có dạng:
c)
Gọi là mặt phẳng qua . Khi đó , là cặp vectơ chỉ phương của .
Ta có: và
Khi đó:
Vậy phương trình mặt phẳng có dạng:
Cách khác:
Mp đi qua ba điểm và có phương trình:
Bài 2 trang 80 SGK Hình học 12: Viết phương trình mặt phẳng trung trực của đoạn thẳng
với
và
.
Phương pháp giải:
Gọi mặt phẳng là mặt phẳng cần tìm. Khi đó mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với hay nhận vecto làm VTPT.
Sau đó ta áp dụng công thức dưới đây để lập phương trình:
Phương trình mặt phẳng đi qua và có VTPT có dạng:
Lời giải:
Gọi là trung điểm của
Khi đó mặt phẳng cần lập đi qua và nhận làm VTPT.
Có và nên phương trình mặt phẳng là:
Bài 3 trang 80 SGK Hình học 12: a) Lập phương trình của các mặt phẳng tọa độ
.
b) Lập phương trình của các mặt phẳng đi qua điểm và lần lượt song song với các mặt phẳng tọa độ.
Phương pháp giải:
a) Phương trình mặt phẳng đi qua và có VTPT có dạng:
b) Cho hai mặt phẳng: thì
Sau đó dựa vào công thức để lập phương trình mặt phẳng cần lập.
Lời giải:
a)
Mặt phẳng qua điểm và có vectơ pháp tuyến nên:
hay .
Tương tự:
:
: .
b)
Mặt phẳng qua điểm song song với mặt phẳng nên nhận làm VTPT.
.
Tương tự mặt phẳng qua và song song với mặt phẳng có phương trình:
.
Mặt phẳng qua song song với mặt phẳng có phương trình:
.
Bài 4 trang 80 SGK Hình học 12: Lập phương trình mặt phẳng :
a) Chứa trục và điểm ;
b) Chứa trục và điểm ;
c) Chứa trục và điểm ;
Phương pháp giải:
+) Mặt phẳng chứa các vecto VTPT của là:
+) Phương trình mặt phẳng đi qua và có VTPT có dạng:
Lời giải:
a)
Gọi là mặt phẳng qua và chứa trục , thì qua điểm và .
Khi đó là vectơ pháp tuyến của .
Phương trình mặt phẳng có dạng: hay .
b)
Mặt phẳng qua điểm và chứa trục thì qua điểm có và là cặp vectơ chỉ phương.
Ta có VTPT của là:
Phương trình mặt phẳng có dạng : hay .
c)
Mặt phẳng qua điểm và chứa trục nên nó đi qua và nhận cặp vectơ và làm vectơ chỉ phương.
Ta có:
Chọn , phương trình mặt phẳng có dạng: hay .
Bài 5 trang 80 SGK Hình học 12: Cho tứ diện có các đỉnh là
a) Hãy viết các phương trình mặt phẳng và
b) Hãy viết phương trình mặt phẳng đi qua cạnh và song song với cạnh .
Phương pháp giải:
Mặt phẳng đi qua điểm và có VTPT:
+) Phương trình mặt phẳng đi qua và có VTPT có dạng:
Lời giải:
a)
Mặt phẳng đi qua và chứa giá của các vectơ và .
Ta có::
Chọn .
Phương trình có dạng: hay .
Tương tự ta có :, và
Chọn là VTPT của mặt phẳng .
Phương trình mặt phẳng có dạng: hay .
b)
Mặt phẳng qua cạnh và song song với thì qua và nhận , làm vectơ chỉ phương.
VTPT của mặt phẳng
Phương trình mặt phẳng có dạng : hay .
Bài 6 trang 80 SGK Hình học 12: Viết phương trình mặt phẳng
đi qua điểm
và song song với mặt phẳng
có phương trình:
.
Phương pháp giải:
+) Cho hai mặt phẳng: thì
+) Phương trình mặt phẳng đi qua và có VTPT có dạng:
Lời giải:
Ta có vectơ là vectơ pháp tuyến của mặt phẳng .
Vì nên cũng là vectơ pháp tuyến của mặt phẳng .
Phương trình mặt phẳng có dạng: hay .
Cách khác:
Vì mặt phẳng (α) song song với mặt phẳng nên phương trình của mp có dạng:
Vì nên
Vậy phương trình của là:
Bài 7 trang 80 SGK Hình học 12: Lập phương trình mặt phẳng
đi qua hai điểm
và vuông góc với mặt phẳng
:
.
Phương pháp giải:
+) Mặt phẳng thì:
+) Mặt phẳng đi qua hai điểm thì:
+) Sử dụng công thức lập phương trình mặt phẳng: Phương trình mặt phẳng đi qua và có VTPT có dạng:
Lời giải:
Ta có:
Theo đề bài ta có:
Mặt phẳng đi qua hai điểm thì:
Ta có:
Mặt phẳng đi qua và nhận vecto làm VTPT có phương trình:
Bài 8 trang 81 SGK Hình học 12: Xác định giá trị của
và
để mỗi cặp mặt phẳng sau đây là một cặp mặt phẳng song song với nhau:
a) và ;
b) và ;
Phương pháp giải:
Cho hai mặt phẳng: và .
Khi đó hay
Lời giải:
a)
Nếu thì nên hai mặt phẳng không song song.
Xét thì hai mặt phẳng và song song với nhau khi và chỉ khi:
b)
Nếu thì nên hai mặt phẳng không song song.
Hai mặt phẳng và song song khi và chỉ khi:
Bài 9 trang 81 SGK Hình học 12: Tính khoảng cách từ điểm
lần lượt đến các mặt phẳng sau:
a) ;
b) ;
c) .
Phương pháp giải:
Cho điểm và mặt phẳng Khi đó khoảng cách từ điểm đến mặt phẳng được tính bởi công thức:
Lời giải:
a)
b)
c)
Bài 10 trang 81 SGK Hình học 12: Giải các bài toán sau đây bằng phương pháp tọa độ.
Cho hình lập phương cạnh bằng
a) Chứng minh rằng hai mặt phẳng và song song với nhau.
b) Tính khoảng cách giữa hai mặt phẳng nói trên.
Phương pháp giải:
a) Chọn hệ trục tọa độ hợp lý sau đó suy ra tọa độ các điểm của hình lập phương.
+) Lập phương trình mặt phẳng đi qua ba điểm có VTPT và mặt phẳng đi qua ba điểm có VTPT
+) Chứng minh hai mặt phẳng này song song ta cần chứng minh cùng phương
b) Hai mặt phẳng và song song nên
+) Sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng để tính.
Lời giải:
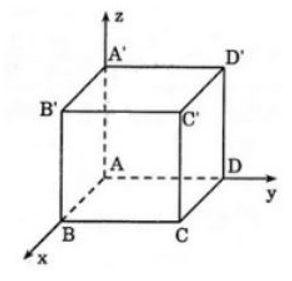
Chọn hệ trục tọa độ như hình vẽ có:
Khi đó:
a) Ta có:
Ta có:
Mặt phẳng đi qua và có VTPT Phương trình mặt phẳng là:
PT hay
Xét phương trình hai mặt phẳng ta có:
Chú ý : Bài này có thể làm không cần phương pháp tọa độ như sau:
Xét hai mặt phẳng và , ta có vì là hình chữ nhật, vì là hình chữ nhật.
Do đó mặt phẳng có hai đường thẳng cắt nhau và lần lượt song song với hai đường thẳng cắt nhau và của mặt phẳng . Vì vậy
b) Vì nên:
Lý thuyết Bài 2: Phương trình mặt phẳng
1. Vectơ pháp tuyến của mặt phẳng.
* Cho mặt phẳng , vectơ mà giá của nó vuông góc với mặt phẳng thì được gọi là vectơ pháp tuyến của mặt phẳng .
* Cho mặt phẳng , cặp vectơ , không cùng phương mà giá của chúng là hai đường thẳng song song hay nằm trong mặt phẳng được gọi là cặp vectơ chỉ phương của mặt phẳng . Khi đó vectơ . là vectơ pháp tuyến của mặt phẳng .
* Nếu , thì :
* Mặt phẳng hoàn toàn được xác định khi biết một điểm và một vectơ pháp tuyến của nó, hay một điểm thuộc mặt phẳng và cặp vectơ chỉ phương của nó.
2. Phương trình mặt phẳng.
* Mặt phẳng qua điểm và nhận làm vectơ pháp tuyến có phương trình có dạng:
* Mọi mặt phẳng trong không gian có phương trình tổng quát có dạng:
Khi đó vectơ là vectơ pháp tuyến của mặt phẳng.
* Mặt phẳng đi qua ba điểm ở đó có phương trình :. Phương trình này còn được gọi là phương trình mặt phẳng theo đoạn chắn.
3. Vị trí tương đối của hai mặt phẳng.
Cho hai mặt phẳng và có phương trình :
Ta có và . Khi đó:
⇔ ⇔
và
và
(nghĩa là và không cùng phương).
4. Khoảng cách từ một điểm đến một mặt phẳng.
Trong không gian cho mặt phẳng có phương trình:
và điểm .Khoảng cách từ M0 đến được cho bởi công thức:
5. Góc giữa hai mặt phẳng.
Cho hai mặt phẳng và có phương trình :
Gọi là góc giữa hai mặt phẳng và thì và :
Sơ đồ tư duy về phương trình mặt phẳng
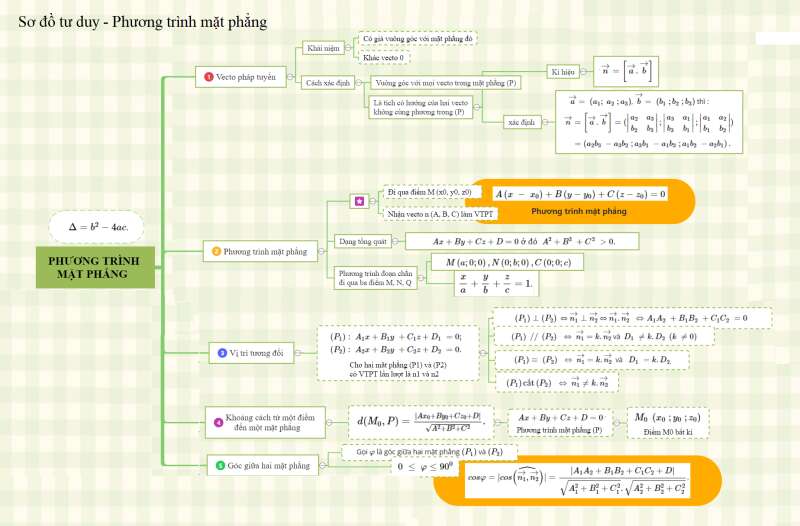
Các dạng toán viết phương trình mặt phẳng
1. Kiến thức cần nhớ
- Phươngtrình mặt phẳng đi qua điểm và nhận làm VTPT là:
Lưu ý: Muốn viết phương trình mặt phẳng ta cần xác định một điểm và một véc tơ pháp tuyến.
- Phương trình đoạn chắn: Mặt phẳng đi qua điểm là:
- Phương trình các mặt phẳng tọa độ:
- Chùm mặt phẳng:
Giả sử trong đó:
Khi đó, mọi mặt phẳng chứa đều có phương trình dạng:với
2. Một số dạng toán thường gặp
Dạng 1: Viết phương trình mặt phẳng.
-) Mặt phẳng đi qua ba điểm.
đi qua đi qua và nhận làm VTPT.
-) Mặt phẳng trung trực của đoạn thẳng.
là mặt phẳng trung trực của nếu đi qua trung điểm của và nhận làm VTPT.
-) Mặt phẳng đi qua một điểm và song song với mặt phẳng.
đi qua và song song nếu đi qua và nhận làm VTPT.
-) Mặt phẳng đi qua hai điểm và vuông góc với một mặt phẳng.
đi qua hai điểm và song song mặt phẳng nếu đi qua và nhận làm VTPT.
-) Mặt phẳng đi qua một điểm và vuông góc với hai mặt phẳng.
đi qua điểm và vuông góc với (không song song) nếu đi qua và nhận làm VTPT.
Dạng 2: Tính khoảng cách giữa hai mặt phẳng song song.
Phương pháp:
- Bước 1: Tìm một điểm nằm trên mặt phẳng này.
- Bước 2: Tính khoảng cách từ điểm đó đến mặt phẳng còn lại.
- Bước 3: Kết luận: khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm thuộc mặt phẳng này đến mặt phẳng kia.
Dạng 3: Tìm điều kiện của tham số để hai mặt phẳng vuông góc, song song, …
Sử dụng các điều kiện để hai mặt phẳng song song, vuông góc,… để tìm tham số.

