Giải Toán 11 Ôn tập chương I

Nguyễn Lê Thục Nhi Ngày: 18-05-2022 Lớp 11

2.2 K

Tailieumoi.vn giới thiệu Giải bài tập Toán 11 Ôn tập chương I chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Ôn tập chương I lớp 11.

Giải bài tập Toán 11 Ôn tập chương I

Bài tập (trang 40, 41 sgk Đại số và Giải tích 11)

Bài 1 trang 40 sgk Đại số và Giải tích 11:

a. Hàm số y = cos3x có phải là hàm số chẵn không? Tại sao?

b. Hàm số

y = \tan (x + \frac{π}{5})

có phải là hàm số lẻ không? Tại sao?

Phương pháp giải:

Hàm số $y = f (x)$ có tập xác định D, với mọi $x \in D \Rightarrow - x \in D$ .

Hàm số được gọi là hàm chẵn khi và chỉ khi: $f (x) = f (- x)$

Hàm số được gọi là hàm lẻ khi và chỉ khi: $- f (x) = f (- x)$

Lưu ý: Các hàm $y = \sin x, y = \tan x, y = \cot x$ là hàm lẻ, hàm số $y = \cos x$ là hàm chẵn.

Lời giải:

a. Ta có:

+) Hàm số $y = c o s 3 x$ có tập xác định là $D = R$

+) $\forall x \in R \Rightarrow - x \in R$

+) $f (- x) = c o s 3 (- x) = c o s (- 3 x) = c o s (3 x) = f (x)$

Vậy hàm số $y = c o s 3 x$ là hàm số chẵn

b. $D K : x + \frac{π}{5} \neq \frac{π}{2} + k π$ $\Leftrightarrow x \neq \frac{3 π}{10} + k π$

Ta có:

+) $y = f (x) = \tan (x + \frac{π}{5})$ có tập xác định là $D = R ∖ {\frac{3 π}{10} + k π, k \in Z}$

+) $\forall x \in D \Rightarrow - x \in D$

$f (- x) = \tan (- x + \frac{π}{5})$ $= \tan [- (x - \frac{π}{5})] = - \tan (x - \frac{π}{5})$

$- f (x) = - \tan (x + \frac{π}{5})$

Dễ thấy $- \tan (x - \frac{π}{5}) \neq - \tan (x + \frac{π}{5})$ khi $x = 0$ nên $f (- x) \neq - f (x)$ hay hàm số không lẻ.

Bài 2 trang 40 sgk Đại số và Giải tích 11: Căn cứ vào đồ thị hàm số

y = s i n x

, tìm các giá trị của

x

trên đoạn

[\frac{- 3 π}{2}, 2 π]

để hàm số đó:

a. Nhận giá trị bằng −1

b. Nhận giá trị âm

Phương pháp giải:

B1: Vẽ đồ thị hàm số $y = s i n x$ trên đoạn $[\frac{- 3 π}{2}, 2 π]$

B2: Vẽ đường thẳng $y = - 1$ , giao điểm của đồ thị với đường thẳng $y = - 1$ chính là giá trị $x$ cần tìm

Lời giải:

Đồ thị hàm số $y = s i n x$ trên đoạn $[\frac{- 3 π}{2}, 2 π]$

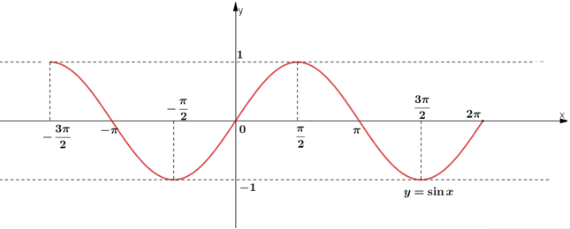
Dựa vào đồ thị hàm số $y = s i n x$

Những giá trị của $x \in$ $[\frac{- 3 π}{2}, 2 π]$ để hàm số $y = s i n x$ nhận giá trị bằng $- 1$ là: $x = \frac{- π}{2}; x = \frac{3 π}{2}$

(Hoành độ giao điểm của đồ thị hàm số và đường thẳng y = -1).

Phương pháp giải:

Quan sát đồ thị, các giá trị nào của x thảo mà đồ

Lời giải:

Những giá trị của $x \in$ $[\frac{- 3 π}{2}, 2 π]$ để hàm số $y = s i n x$ nhận giá trị âm là: $x \in (- π, 0) \cup (π, 2 π)$ .

(Các khoảng mà đồ thị nằm phía dưới trục hoành).

Bài 3 trang 41 sgk Đại số và Giải tích 11: Tìm giá trị lớn nhất của các hàm số sau:

Phương pháp giải:

Dựa vào tính chất:

- 1 \leq \sin x \leq 1; - 1 \leq \cos x \leq 1

Lời giải:

Ta có:

$\begin{aligned} - 1 \leq \cos x \leq 1, \forall x \in R \\ \Leftrightarrow 0 \leq 1 + \cos x \leq 2 \\ \Leftrightarrow 0 \leq 2 (1 + \cos x) \leq 4 \\ \Leftrightarrow 0 \leq \sqrt{2 (1 + \cos x)} \leq 2 \\ \Leftrightarrow 1 \leq \sqrt{2 (1 + \cos x)} + 1 \leq 3 \end{aligned}$

$\Rightarrow y_{m a x} = 3$

Dấu “ = “ xảy ra $\Leftrightarrow c o s x = 1 \Leftrightarrow x = k 2 π (k \in Z)$

Vậy $y_{m a x} = 3$ khi $x = k 2 π$

Phương pháp giải:

Dựa vào tính chất:

- 1 \leq \sin x \leq 1; - 1 \leq \cos x \leq 1

Lời giải:

Ta có:

Với mọi $x \in R$ , ta có:

$\begin{aligned} - 1 \leq \sin (x - \frac{π}{6}) \leq 1 \\ \Leftrightarrow - 3 \leq 3 \sin (x - \frac{π}{6}) \leq 3 \\ \Leftrightarrow - 5 \leq 3 \sin (x - \frac{π}{6}) - 2 \leq 1 \\ \Leftrightarrow - 5 \leq y \leq 1 \end{aligned}$

Vậy $y_{m a x} = 1$ $\Leftrightarrow \sin (x - \frac{π}{6}) = 1$

$\Leftrightarrow x - \frac{π}{6} = \frac{π}{2} + k 2 π \Leftrightarrow x = \frac{2 π}{3} + k 2 π (k \in Z)$

Bài 4 trang 41 sgk Đại số và Giải tích 11: Giải các phương trình:

\sin (x + 1) = \frac{2}{3}

b. $\sin^{2} 2 x = \frac{1}{2}$

c. $\cot^{2} \frac{x}{2} = \frac{1}{3}$

d. $\tan (\frac{π}{12} + 12 x) = - \sqrt{3}$

Phương pháp giải:

Giải phương trình lượng giác cơ bản của hàm sin.

Lời giải:

Ta có:

$\begin{aligned} \sin (x + 1) = \frac{2}{3} \\ \Leftrightarrow [\begin{matrix} x + 1 = \arcsin \frac{2}{3} + k 2 π \\ x + 1 = π - \arcsin \frac{2}{3} + k 2 π \end{matrix} \\ \Leftrightarrow [\begin{matrix} x = - 1 + \arcsin \frac{2}{3} + k 2 π \\ x = - 1 + π - \arcsin \frac{2}{3} + k 2 π \end{matrix}; k \in Z \end{aligned}$

Vậy nghiệm của phương trình là $x = - 1 + \arcsin \frac{2}{3} + k 2 π;$ $x = - 1 + π - \arcsin \frac{2}{3} + k 2 π (k \in Z)$

Phương pháp giải:

Sử dụng công thức hạ bậc.

Lời giải:

Ta có:

$\begin{aligned} \sin^{2} 2 x = \frac{1}{2} \Leftrightarrow \frac{1 - \cos 4 x}{2} = \frac{1}{2} \\ \Leftrightarrow \cos 4 x = 0 \Leftrightarrow 4 x = \frac{π}{2} + k π \\ \Leftrightarrow x = \frac{π}{8} + k \frac{π}{4}, k \in Z \end{aligned}$

Vậy nghiệm của phương trình là $x = \frac{π}{8} + \frac{k π}{4} (k \in Z)$ .

Cách khác:

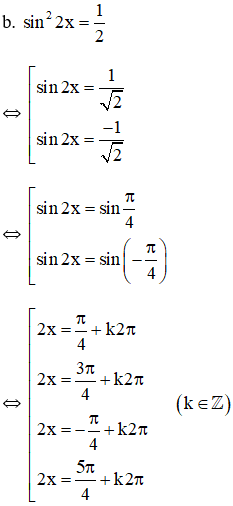
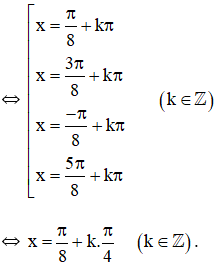
Có thể để nguyên các họ nghiệm không nhất thiết phải gộp nghiệm.

Phương pháp giải:

Lấy căn bậc hai hai vế. Giải phương trình lượng giác cơ bản của hàm cot.

Lời giải:

$D K : \frac{x}{2} \neq k π \Leftrightarrow x \neq k 2 π$

Ta có:

$\begin{aligned} \cot^{2} \frac{x}{2} = \frac{1}{3} \Leftrightarrow [\begin{matrix} \cot \frac{x}{2} = \frac{\sqrt{3}}{3} (1) \\ \cot \frac{x}{2} = - \frac{\sqrt{3}}{3} (2) \end{matrix} \\ (1) \Leftrightarrow \cot \frac{x}{2} = \cot \frac{π}{3} \\ \Leftrightarrow \frac{x}{2} = \frac{π}{3} + k π \\ \Leftrightarrow x = \frac{2 π}{3} + k 2 π, k \in Z \\ (2) \Leftrightarrow \cot \frac{x}{2} = \cot (- \frac{π}{3}) \\ \Leftrightarrow \frac{x}{2} = - \frac{π}{3} + k π \\ \Leftrightarrow x = - \frac{2 π}{3} + k 2 π; k \in Z (T M) \end{aligned}$

Vậy nghiệm của phương trình là $x = \pm \frac{2 π}{3} + k 2 π (k \in Z)$ .

Chú ý:

$\cot (- \frac{\sqrt{3}}{3}) = \cot (\frac{2 π}{3})$ nên khi giải pt (2) cũng có thể đưa về góc $\frac{2 π}{3}$ .

Phương pháp giải:

Giải phương trình lượng giác cơ bản của hàm tan.

Lời giải:

$D K : \frac{π}{12} + 12 x \neq \frac{π}{2} + k π$ $\Leftrightarrow 12 x \neq \frac{5 π}{12} + k π$ $\Leftrightarrow x \neq \frac{5 π}{144} + \frac{k π}{12}$

Ta có:

$\tan (\frac{π}{12} + 12 x) = - \sqrt{3}$

$\Leftrightarrow \tan (\frac{π}{12} + 12 x) = \tan (\frac{- π}{3})$
$\Leftrightarrow \frac{π}{12} + 12 x = \frac{- π}{3} + k π$

$\Leftrightarrow x = - \frac{5 π}{144} + k \frac{π}{12}, k \in Z (T M)$

Vậy nghiệm của phương trình đã cho là: $x = \frac{- 5 π}{144} + \frac{k π}{12}, k \in Z$

Bài 5 trang 41 sgk Đại số và Giải tích 11: Giải các phương trình sau:

Phương pháp giải:

Đặt

t = \cos x

, đưa về phương trình bậc hai ẩn t.

Lời giải:

$2 c o s^{2} x - 3 c o s x + 1 = 0$

Đặt $t = c o s x$ với điều kiện $- 1 \leq x \leq 1$ , khi đó ta có:

$2 t^{2} - 3 t + 1 = 0 \Leftrightarrow [\begin{matrix} t = 1 \\ t = \frac{1}{2} \end{matrix}$

Với $t = 1$ , ta có: $c o s x = 1 \Leftrightarrow x = k 2 π, k \in Z$

Với $t = \frac{1}{2}$ ta có: $\cos x = \frac{1}{2} \Leftrightarrow x = \pm \frac{π}{3} + k 2 π (k \in Z)$

Vậy phương trình đã cho có nghiệm là: $x = k 2 π, x = \pm \frac{π}{3} + k 2 π, k \in Z$

Phương pháp giải:

Đưa phương trình về dạng phương trình tích.

Lời giải:

Ta có:

$25 s i n^{2} x + 15 s i n 2 x + 9 c o s^{2} x = 25$

$\Leftrightarrow 25 (1 - c o s^{2} x) + 15.2 s i n x c o s x + 9 c o s^{2} x = 25$

$\Leftrightarrow 25 - 25 \cos^{2} x + 30 \sin x \cos x + 9 \cos^{2} x - 25 = 0$

$\Leftrightarrow - 25 c o s^{2} x + 30 s i n x c o s x + 9 c o s^{2} x = 0$

$\Leftrightarrow - 16 c o s^{2} x + 30 s i n x c o s x = 0$

$\begin{aligned} \Leftrightarrow - 2 \cos x (8 \cos x - 15 \sin x) = 0 \\ \Leftrightarrow [\begin{matrix} \cos x = 0 \\ 8 \cos x - 15 \sin x = 0 \end{matrix} \\ \Leftrightarrow [\begin{array}{l} \cos x = 0 \\ 8 \cos x = 15 \sin x \end{array} \\ \Leftrightarrow [\begin{array}{l} \cos x = 0 \\ \frac{8}{15} = \frac{\sin x}{\cos x} \end{array} \\ \Leftrightarrow [\begin{matrix} \cos x = 0 \\ \tan x = \frac{8}{15} \end{matrix} \\ \Leftrightarrow [\begin{matrix} x = \frac{π}{2} + k π \\ x = \arctan \frac{8}{15} + k π \end{matrix}, k \in Z \end{aligned}$

Vậy nghiệm của phương trình là $x = \frac{π}{2} + k π, x = \arctan \frac{8}{15} + k π (k \in Z)$

Phương pháp giải:

Phương trình dạng

a \sin x + b \cos x = c

, chia cả 2 vế cho

\sqrt{a^{2} + b^{2}}

Lời giải:

Chia cả hai vế của phương trình cho $\sqrt{5}$ , ta được:

$\frac{2}{\sqrt{5}} \sin x + \frac{1}{\sqrt{5}} \cos x = \frac{1}{\sqrt{5}}$ (*)

Vì ${(\frac{2}{\sqrt{5}})}^{2} + {(\frac{1}{\sqrt{5}})}^{2} = 1$ nên tồn tại một góc $α$ thỏa mãn:

${\begin{matrix} \sin α = \frac{2}{\sqrt{5}} \\ \cos α = \frac{1}{\sqrt{5}} \end{matrix}$

Khi đó, phương trình (*) trở thành:

$\begin{array}{l} \sin x \sin α + \cos x \cos α = \cos α \\ \Leftrightarrow \cos (x - α) = \cos α \\ \Leftrightarrow [\begin{array}{l} x - α = α + k 2 π \\ x - α = - α + k 2 π \end{array} \\ \Leftrightarrow [\begin{array}{l} x = 2 α + k 2 π \\ x = k 2 π \end{array} (k \in Z) \end{array}$

Vậy nghiệm của phương trình là: $x = 2 α + k 2 π; x = k 2 π$ $(k \in Z)$ .

Phương pháp giải:

Biến đổi, quy đồng, đưa phương trình về dạng phương trình bậc cao đối với 1 hàm số lượng giác.

Lời giải:

Điều kiện $s i n x \neq 0 \Leftrightarrow x \neq k π, k \in Z$ .

Phương trình đã cho biến đổi:

$\begin{aligned} \sin x + \frac{3}{2} . \frac{\cos x}{\sin x} = 0 \\ \Leftrightarrow 2 \sin^{2} x + 3 \cos x = 0 \\ \Leftrightarrow 2 (1 - \cos^{2} x) + 3 \cos x = 0 \\ \Leftrightarrow 2 \cos^{2} x - 3 \cos x - 2 = 0 (*) \end{aligned}$

Đặt $t = c o s x$ với điều kiện $- 1 \leq t \leq 1$

Khi đó, phương trình (*) trở thành:

$2 t^{2} - 3 t - 2 = 0 \Leftrightarrow [\begin{matrix} t = 2 (loại) \\ t = \frac{- 1}{2} (t m) \end{matrix}$

Với $t = - \frac{1}{2} \Leftrightarrow \cos x = - \frac{1}{2}$ $\Leftrightarrow x = \pm \frac{2 π}{3} + k 2 π (k \in Z)$

Bài 6 trang 41 sgk Đại số và Giải tích 11: Phương trình

\cos x = \sin x

có số nghiệm thuộc đoạn

[- π, π]

là:

(A). $2$ (B). $4$

(C). $5$ (D). $6$

Phương pháp giải:

Đưa phương trình về dạng phương trình cơ bản của hàm tan.

Lời giải:

Ta có: $\sin x = \cos x \Leftrightarrow \tan x = 1$ $\Leftrightarrow x = \frac{π}{4} + k π (k \in Z)$

Vì $x \in [- π, π]$ nên:

$- π \leq \frac{π}{4} + k π \leq π \Leftrightarrow - 1 \leq \frac{1}{4} + k \leq 1$

$\Leftrightarrow - \frac{5}{4} \leq k \leq \frac{3}{4}$

Ta có: $k \in Z$ nên $k \in {- 1; 0}$ .

Suy ra phương trình đã cho có hai nghiệm thuộc $[- π, π]$ là $x = - \frac{3 π}{4}; x = \frac{π}{4}$

Chọn đáp án A.

Bài 7 trang 41 sgk Đại số và Giải tích 11: Phương trình

\frac{\cos 4 x}{\cos 2 x} = \tan 2 x

có số nghiệm thuộc khoảng

(0; \frac{π}{2})

là:

A. $2$ B. $3$

C. $4$ D.

Phương pháp giải:

+) Sử dụng công thức $\tan 2 x = \frac{\sin 2 x}{\cos 2 x}$ , quy đồng, bỏ mẫu.

+) Sử dụng công thức nhân đôi: $\cos 4 x = 1 - 2 \sin^{2} 2 x$

+) Giải phương trình bậc hai của $\sin 2 x$ .

+) Giải phương trình lượng giác cơ bản của hàm sin.

Lời giải:

Điều kiện: $c o s 2 x \neq 0 \Leftrightarrow s i n 2 x \neq \pm 1$

Ta có:

$\frac{\cos 4 x}{\cos 2 x} = \frac{\sin 2 x}{\cos 2 x} \Rightarrow \cos 4 x = \sin 2 x$

$\Leftrightarrow 1 - 2 s i n^{2} 2 x = \sin 2 x$

$\Leftrightarrow 2 \sin^{2} 2 x + \sin 2 x - 1 = 0$

$\Leftrightarrow [\begin{matrix} \sin 2 x = - 1 (loại) \\ \sin 2 x = \frac{1}{2} \end{matrix}$

Ta có:

$\begin{aligned} \sin 2 x = \frac{1}{2} = \sin \frac{π}{6} \\ \Leftrightarrow [\begin{matrix} 2 x = \frac{π}{6} + k 2 π \\ 2 x = π - \frac{π}{6} + k 2 π \end{matrix} \Leftrightarrow [\begin{matrix} x = \frac{π}{12} + k π \\ x = \frac{5 π}{12} + l π \end{matrix} k, l \in Z \end{aligned}$

Ta lại có:

$x \in (0, \frac{π}{2})$

+) $x = \frac{π}{12} + k π : 0 < \frac{π}{12} + k π < \frac{π}{2}$

$\Leftrightarrow 0 < \frac{1}{12} + k < \frac{1}{2}$

$\Leftrightarrow \frac{- 1}{12} < k < \frac{5}{12} (k \in Z) \Rightarrow k = 0$

$\Rightarrow x = \frac{π}{12}$

+) $x = \frac{5 π}{12} + l π : 0 < \frac{5 π}{12} + l π < \frac{π}{2}$

$\Leftrightarrow 0 < \frac{5}{12} + l < \frac{1}{2}$

$\Leftrightarrow \frac{- 5}{12} < l < \frac{1}{12} (l \in Z) \Rightarrow l = 0$

$\Rightarrow x = \frac{5 π}{12}$

Vậy phương trình có đúng $2$ nghiệm thuộc khoảng $(0, \frac{π}{2})$

Chọn đáp án A.

Bài 8 trang 41 sgk Đại số và Giải tích 11: Nghiệm dương nhỏ nhất của phương trình

\sin x + \sin 2 x = \cos x + 2 \cos^{2} x

là:

A. $\frac{π}{6}$ B. $\frac{2 π}{3}$

C. $\frac{π}{4}$ D. $\frac{π}{3}$

Phương pháp giải:

Đưa phương trình về dạng tích, sau đó giải các phương trình lượng giác cơ bản, sử dụng công thức nhân đôi $\sin 2 x = 2 \sin x \cos x$ .

Sau khi tìm được các họ nghiệm, đối với mỗi họ nghiệm ta tìm nghiệm dương nhỏ nhất và chọn đáp án đúng.

Lời giải:

Ta có:

$s i n x + s i n 2 x = c o s x + 2 c o s^{2} x$

$\Leftrightarrow s i n x + 2 s i n x c o s x = c o s x + 2 c o s^{2} x$

$\Leftrightarrow s i n x (1 + 2 c o s x) = c o s (1 + 2 c o s x)$

$\Leftrightarrow (1 + 2 c o s x) (s i n x - c o s x) = 0$

$\Leftrightarrow [\begin{matrix} 1 + 2 \cos x = 0 \\ \sin x - \cos x = 0 \end{matrix} \Leftrightarrow [\begin{matrix} \cos x = - \frac{1}{2} \\ \tan x = 1 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \pm \frac{2 π}{3} + k 2 π \\ x = \frac{π}{4} + k π \end{matrix} (k \in Z)$

Nghiệm dương nhỏ nhất của họ nghiệm : $x = \frac{2 π}{3} + k 2 π \Rightarrow x = \frac{2 π}{3}$

Nghiệm dương nhỏ nhất của họ nghiệm: $x = - \frac{2 π}{3} + k 2 π \Rightarrow x = - \frac{2 π}{3} + 2 π = \frac{4 π}{3}$

Nghiệm dương nhỏ nhất của họ nghiệm: $x = \frac{π}{4} + k π \Rightarrow x = \frac{π}{4}$

Suy ra nghiệm dương nhỏ nhất của phương trình đã cho là $x = \frac{π}{4}$

Chọn đáp án C.

Cách khác:

Thay các nghiệm ở mỗi đáp án vào phương trình ta thấy chỉ có nghiệm $x = \frac{π}{4}, x = \frac{2 π}{3}$ thỏa mãn phương trình.

Do $\frac{π}{4} < \frac{2 π}{3}$ nên ta chọn nghiệm $x = \frac{π}{4}$ .

Bài 9 trang 41 sgk Đại số và Giải tích 11: Nghiệm âm lớn nhất của phương trình

2 \tan^{2} x + 5 \tan x + 3 = 0

là:

A. $\frac{- π}{3}$ B. $\frac{- π}{4}$

C. $\frac{- π}{6}$ D. $\frac{- 5 π}{6}$

Phương pháp giải:

B1: Đặt $t = \tan x$ , giải phương trình bậc hai ẩn t.

B2: Giải phương trình lượng giác cơ bản và biểu diễn các nghiệm trên đường tròn lượng giác.

Lời giải:

Ta có:

$\begin{array}{l} 2 \tan^{2} x + 5 \tan x + 3 = 0 \\ \Leftrightarrow [\begin{array}{l} \tan x = - 1 \\ \tan x = - \frac{3}{2} \end{array} \\ \tan x = - 1 \Leftrightarrow x = - \frac{π}{4} + k π \\ \tan x = - \frac{3}{2} \Leftrightarrow x = \arctan (- \frac{3}{2}) + k π \end{array}$

Nghiệm âm lớn nhất của họ nghiệm $x = - \frac{π}{4} + k π$ là $x = - \frac{π}{4}$ .

Nghiệm âm lớn nhất của họ nghiệm $x = \arctan (- \frac{3}{2}) + k π$ là $x = \arctan (- \frac{3}{2})$

Mà $\arctan (- \frac{3}{2}) \approx - 0, 983,$ $- \frac{π}{4} \approx - 0, 785 \Rightarrow - \frac{π}{4} > \arctan (- \frac{3}{2})$

Vậy nghiệm âm lớn nhất của pt là $x = - \frac{π}{4}$ .

Cách khác:

Dựa vào đường tròn lượng giác ta có:

x = - \frac{π}{4}

là nghiệm âm lớn nhất của phương trình đã cho.

Bài 10 trang 41 sgk Đại số và Giải tích 11: Phương trình

2 \tan x - 2 \cot x - 3 = 0

có số nghiệm thuộc khoảng

(\frac{- π}{2}, π)

là:

A. $1$ B. $2$ C. $3$ D. $4$

Phương pháp giải:

B1: Đưa về phương trình bậc hai của tanx bằng công thức $\cot x = \frac{1}{\tan x}$ .

B2: Giải PT lượng giác , lấy các nghiệm thuộc khoảng $(\frac{- π}{2}, π)$ và KL.

Lời giải:

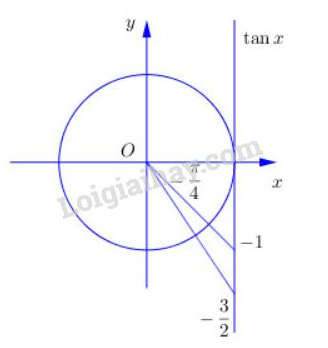
Ta có:

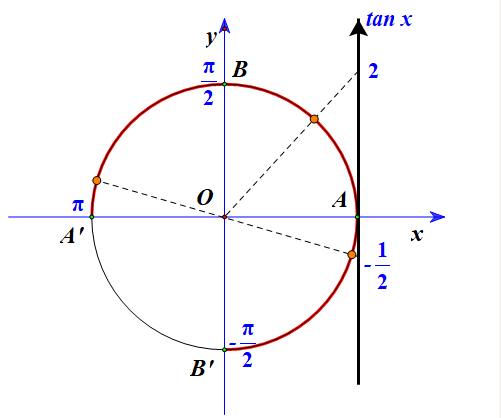
$\begin{aligned} 2 \tan x - 2 \cot x - 3 = 0 \\ \Leftrightarrow 2 \tan x - \frac{2}{\tan x} - 3 = 0 \\ \Rightarrow 2 \tan^{2} x - 3 \tan x - 2 = 0 \\ \Leftrightarrow [\begin{matrix} \tan x = 2 \\ \tan x = \frac{- 1}{2} \end{matrix} \end{aligned}$

Vẽ đường tròn lượng giác với giá trị $t a n x = 2$ , $\tan x = \frac{- 1}{2}$ ta thấy phương trình có ba nghiệm thuộc khoảng $(\frac{- π}{2}, π)$ .

Cách khác:

$[\begin{array}{l} \tan x = 2 \\ \tan x = - \frac{1}{2} \end{array} \Leftrightarrow [\begin{array}{l} x = \arctan 2 + k π \\ x = \arctan (- \frac{1}{2}) + k π \end{array}$

$\begin{array}{l} +) - \frac{π}{2} < \arctan 2 + k π < π \\ \Leftrightarrow - \frac{π}{2} - \arctan 2 < k π < π - \arctan 2 \\ \Leftrightarrow \frac{- \frac{π}{2} - \arctan 2}{π} < k < \frac{π - \arctan 2}{π} \\ \Rightarrow - 0, 85 < k < 0, 65 \\ \Rightarrow k = 0 \\ \Rightarrow x = \arctan 2 \\ +) - \frac{π}{2} < \arctan (- \frac{1}{2}) + k π < π \\ \Leftrightarrow - \frac{π}{2} - \arctan (- \frac{1}{2}) < k π < π - \arctan (- \frac{1}{2}) \\ \Leftrightarrow \frac{- \frac{π}{2} - \arctan (- \frac{1}{2})}{π} < k < \frac{π - \arctan (- \frac{1}{2})}{π} \\ \Rightarrow - 0, 35 < k < 1, 15 \\ \Rightarrow k \in {0; 1} \\ \Rightarrow x \in {\arctan (- \frac{1}{2}); \arctan (- \frac{1}{2}) + π} \end{array}$

Vậy có ba nghiệm cần tìm.

Chọn đáp án C.

Đọc thêm: Kĩ năng tổng hợp và loại nghiệm bằng đường tròn lượng giác

1. Lý thuyết

2. Ví dụ

Tìm và biểu diễn các nghiệm của phương trình sau trên đường tròn lượng giác:

a) $\sin (2 x + \frac{π}{3}) = \frac{1}{2}$ $\Leftrightarrow [\begin{array}{l} 2 x + \frac{π}{3} = \frac{π}{6} + k 2 π \\ 2 x + \frac{π}{3} = \frac{5 π}{6} + k 2 π \end{array}$ $\Leftrightarrow [\begin{array}{l} x = - \frac{π}{12} + k π \\ x = \frac{π}{4} + k π \end{array}, k \in Z$ .

Biểu diễn nghiệm trên đường tròn đơn vị:

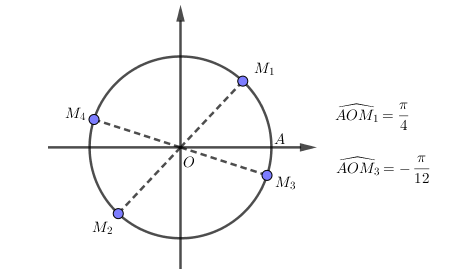
Ở đó, hai điểm $M_{1}, M_{2}$ biểu diễn góc $x = \frac{π}{4} + k π$ và hai điểm $M_{3}, M_{4}$ biểu diễn góc $x = - \frac{π}{12} + k π$ .

b) $\frac{2 \cos 2 x}{1 - \sin 2 x} = 0$

Điều kiện: $1 - \sin 2 x \neq 0 \Leftrightarrow \sin 2 x \neq 1$ $\Leftrightarrow 2 x \neq \frac{π}{2} + k 2 π \Leftrightarrow x \neq \frac{π}{4} + k π$ .

Phương trình $\Leftrightarrow \cos 2 x = 0 \Leftrightarrow 2 x = \frac{π}{2} + k π$ $\Leftrightarrow x = \frac{π}{4} + \frac{k π}{2}$ .

Biểu diễn trên đường tròn đơn vị:

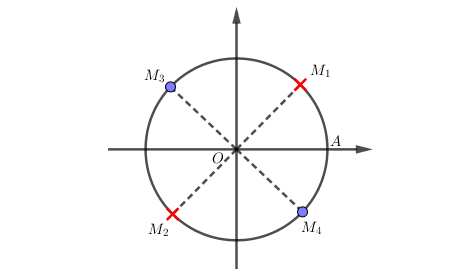
Các điểm biểu diễn $x = \frac{π}{4} + k π$ là $M_{1}, M_{2}$ nhưng điều kiện là $x \neq \frac{π}{4} + k π$ nên hai điểm này không lấy.

Các điểm biểu diễn $x = \frac{π}{4} + \frac{k π}{2}$ là $M_{1}, M_{2}, M_{3}, M_{4}$ nhưng do không lấy hai điểm $M_{1}, M_{2}$ nên các điểm biểu diễn nghiệm chỉ còn $M_{3}, M_{4}$ .

Dễ thấy hai điểm này đối xứng nhau qua $O$ và $\hat{A O M_{4}} = - \frac{π}{4}$ nên nghiệm của phương trình là $x = - \frac{π}{4} + k π, k \in Z$ .

c) $\frac{\sqrt{3} \cot 2 x - 1}{2 \cos x + 1} = 0$

Điều kiện: $2 \cos x + 1 \neq 0 \Leftrightarrow \cos x \neq - \frac{1}{2}$ $\Leftrightarrow {\begin{cases} x \neq \frac{2 π}{3} + k 2 π \\ x \neq - \frac{2 π}{3} + k 2 π \end{cases}, k \in Z$ .

Khi đó phương trình $\Leftrightarrow \sqrt{3} \cot 2 x - 1 = 0 \Leftrightarrow \cot 2 x = \frac{1}{\sqrt{3}}$ $\Leftrightarrow \cot 2 x = \cot \frac{π}{3} \Leftrightarrow 2 x = \frac{π}{3} + k π$ $\Leftrightarrow x = \frac{π}{6} + \frac{k π}{2}, k \in Z$ .

Biểu diễn trên đường tròn đơn vị:

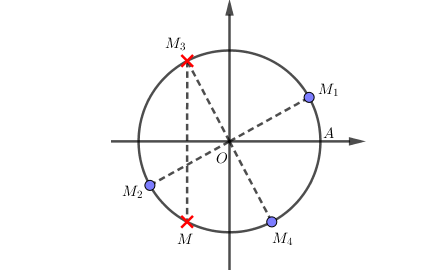
Ở đó, điểm $M$ biểu diễn góc $x = \frac{2 π}{3} + k 2 π$ và điểm $M_{3}$ biểu diễn góc $x = - \frac{2 π}{3} + k 2 π$ , ta đánh dấu đỏ thể hiện không lấy hai điểm đó (do điều kiện xác định).

Các điểm $M_{1}, M_{2}, M_{3}, M_{4}$ là các điểm biểu diễn nghiệm $x = \frac{π}{6} + \frac{k π}{2}$ , trong đó không lấy điểm $M_{3}$ do điều kiện xác định.

Do đó, chỉ còn lại hai điểm $M_{1}, M_{2}$ (với $\hat{A O M_{1}} = \frac{π}{6}$ ) biểu diễn góc $x = \frac{π}{6} + k π$ và điểm $M_{4}$ biểu diễn góc $x = - \frac{π}{3} + k 2 π$ (với $\hat{A O M_{4}} = - \frac{π}{3}$ ).