Với giải sách bài tập Toán 10 Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển

Giải SBT Toán 10 trang 66 Tập 2

Bài 9.7 trang 66 SBT Toán 10 Tập 2: Tại một quán ăn, lúc đầu có 50 khách trong đó có 2x đàn ông và y phụ nữ. Sau một tiếng, y – 6 đàn ông ra về và 2x – 5 khách mới đến là nữ. Chọn ngẫu nhiên một khách. Biết rằng xác suất để chọn được một khách nữ là $\frac{9}{13}$ . Tìm x và y.

Lời giải:

Theo đề bài ta có:

2x + y = 50 ⇔ y = 50 – 2x.

Sau một tiếng, trong quán có:

50 – (y – 6) + 2x – 5

= 50 – y + 6 + 2x – 5

= 51 + 2x – y (người)

Trong đó, có (2x – 5 + y) người là nữ. Vậy ta có xác suất để chọn được một khách nữ là:

$\frac{2x-5+y}{51+2x-y}=\frac{9}{13}$

⇔ 459 + 18x – 9y = 26x – 65 + 13y

⇔ 4x + 11y = 262

Mà y = 50 – 2x nên ta có:

4x + 11 . (50 – 2x) = 262

⇔ 18x = 288

⇔ x = 16

Do đó, y = 50 – 2 . 16 =  18.

Vậy x = 16, y = 18.

Bài 9.8 trang 66 SBT Toán 10 Tập 2: Một lớp có 40 học sinh trong đó có 16 nam. Trong các em nam có 3 em thuận tay trái. Trong các em nữ có 2 em thuận tay trái. Chọn ngẫu nhiên hai em. Tính xác suất để hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái.

Lời giải:

Số cách để chọn ngẫu nhiên hai em trong 40 em học sinh là: $C_{40}^2$ = 780 (cách).

Do đó, ta có n(Ω) = 780.

Gọi A là biến cố: “Hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái”

Lớp có 40 – 16 = 24 em nữ, trong đó, 24 – 2 = 22 em không thuận tay trái. Do đó, số cách chọn 1 em nữ không thuận tay trái là 22 cách.

Trong lớp có 3 em nam thuận tay trái, do đó, số cách chọn 1 em nam thuận tay trái là 3 cách.

Theo quy tắc nhân ta có: n(A) = 22 . 3 = 66.

Vậy xác suất của biến cố A là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{66}{780}=\frac{11}{130}$ .

Bài 9.9 trang 66 SBT Toán 10 Tập 2: Có ba chiếc hộp trong đó hộp I có một viên bi đỏ, một viên bi xanh, một viên bi vàng; hộp II có một viên bi xanh, một viên bi vàng, hộp III có một viên bi đỏ và một viên bi xanh. Tất cả các viên bi đều có cùng kích thước. Từ mỗi hộp rút ngẫu nhiên một viên bi.

a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.

b) Tính xác suất để trong ba viên bi rút ra có ít nhất một viên bi đỏ bằng cách tính gián tiếp thông qua tính xác suất của biến cố đối.

Lời giải:

a)

Kí hiệu Đ, X, V tương ứng là viên bi màu đỏ, xanh, vàng.

Ta có sơ đồ hình cây mô tả các phần tử của không gian mẫu:

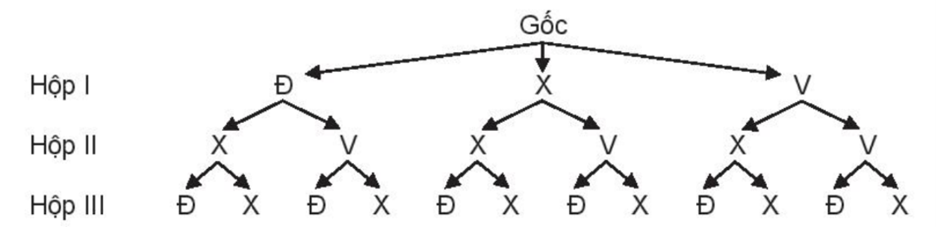
Do đó, ta có:

Ω = {(ĐXĐ; ĐXX; ĐVĐ; ĐVX; XXĐ; XXX; XVĐ; XVX; VXĐ; VXX; VVĐ; VVX}.

Vậy n(Ω) = 12.

b)

Gọi biến cố A: “Trong ba viên bi rút ra có ít nhất một viên bi đỏ”

Biến cố đối của A là $\overline{A}$ : “Trong ba viên bi rút ra không có viên bi màu đỏ”.

Ta có: $\overline{A}$  = {XXX; XVX; VXX; VVX}; n( $\overline{A}$) = 4.

Do đó, ta có: P( $\overline{A}$) = $\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{4}{12}=\frac{1}{3}$ .

Vậy P(A) = $1-P\left(\overline{A}\right)=1-\frac{1}{3}=\frac{2}{3}$ .

Bài 9.10 trang 66 SBT Toán 10 Tập 2: Có ba hộp đựng thẻ. Hộp I chứa các tấm thẻ đánh số {1; 2; 3}. Hộp II chứa các tấm thẻ đánh số {2; 4; 6; 8}. Hộp III chứa các tấm thẻ đánh số {1; 3; 5; 7; 9; 11}. Từ mỗi hộp rút ngẫu nhiên một tấm thẻ rồi cộng ba số trên ba tấm thẻ với nhau. Tính xác suất để kết quả là một số lẻ.

Lời giải:

Gọi a là số trên thẻ rút được từ hộp I, a ∈ {1; 2; 3}.

Gọi b là số trên thẻ rút được từ hộp II, b ∈ {2; 4; 6; 8}.

Gọi c là số trên thẻ rút được từ hộp III, c ∈ {1; 3; 5; 7; 9; 11}.

Ta có không gian mẫu: Ω = {(a, b, c) | a ∈ {1; 2; 3}, b ∈ {2; 4; 6; 8}, c ∈ {1; 3; 5; 7; 9; 11}}.

Theo quy tắc nhân, ta có: n(Ω) = 3 . 4 . 6 = 72.

Xét biến cố A: “Tổng ba số trên ba tấm thẻ là số lẻ”.

Do b luôn là một số chẵn và c luôn là một số lẻ nên tổng b + c luôn là một số lẻ, do đó để (a + b + c) là một số lẻ thì a phải là số chẵn. Do đó, a = 2.

Khi đó, A = {(2, b, c) | b ∈ {2; 4; 6; 8}, c ∈ {1; 3; 5; 7; 9; 11}}.

Do đó, n(A) = 1 . 4 . 6 = 24.

Vậy P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{24}{72}=\frac{1}{3}$ .

Bài 9.11 trang 66 SBT Toán 10 Tập 2: Trên một dãy phố có 3 quán ăn A, B, C. Hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán để ăn trưa.

a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.

b) Tính xác suất của các biến cố sau:

E: “Hai người cùng vào một quán”.

F: “Cả hai không chọn quán C”.

Lời giải:

a) Sơ đồ hình cây mô tả các phần tử của không gian mẫu là:

b)

Ta có không gian mẫu là:

Ω = {AA; AB; AC; BA; BB; BC; CA; CB; CC}.

Suy ra, n(Ω) = 9.

Ta có biến cố E: “Hai người cùng vào một quán”.

Do đó, E = {AA; BB; CC}; n(E) = 3.

Vậy P(E) = $\frac{n\left(E\right)}{n\left(\Omega \right)}=\frac{3}{9}=\frac{1}{3}$ .

Ta có biến cố F: “Cả hai không chọn quán C”.

Do đó, F = {AA; AB; BA; BB}; n(F) = 4.

Vậy P(F) = $\frac{n\left(F\right)}{n\left(\Omega \right)}=\frac{4}{9}$ .

Bài 9.12 trang 66 SBT Toán 10 Tập 2: Trên một phố có hai quán ăn A, B. Bốn bạn Sơn, Hải, Văn, Đạo mỗi người chọn ngẫu nhiên một quán ăn.

a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.

b) Tính xác suất để:

• Tất cả đều vào một quán;

• Mỗi quán có đúng 2 bạn vào;

• Quán A có 3 bạn vào, quán B có 1 bạn vào;

• Một quán có 3 bạn vào, quán kia có 1 bạn vào.

Lời giải:

a) Sơ đồ hình cây mô tả các phần tử của không gian mẫu là:

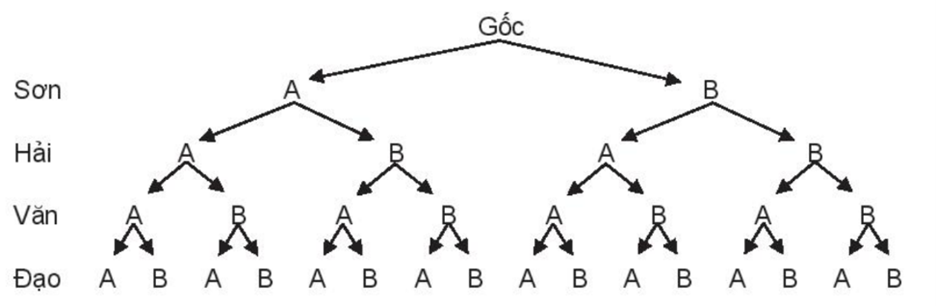
b)

Ta có không gian mẫu:

Ω = {AAAA; AAAB; AABA; AABB; ABAA; ABAB; ABBA; ABBB; BAAA; BAAB; BABA; BABB; BBAA; BBAB; BBBA; BBBB}.

Do đó, n(Ω) = 16.

Gọi biến cố E: “Tất cả đều vào một quán”. Ta có:

E = {AAAA; BBBB}, n(E) = 2, suy ra P(E) = $\frac{n\left(E\right)}{n\left(\Omega \right)}=\frac{2}{16}=\frac{1}{8}$ .

Gọi biến cố F: “Mỗi quán có đúng hai bạn vào”. Ta có:

F = {AABB; ABAB; ABBA; BAAB; BABA; BBAA}, n(F) = 6,

suy ra P(F) = $\frac{n\left(F\right)}{n\left(\Omega \right)}=\frac{6}{16}=\frac{3}{8}$ .

Gọi biến cố G: “Quán A có 3 bạn vào, quán B có 1 bạn vào”. Ta có:

G = {AAAB; AABA; ABAA; BAAA}, n(G) = 4, suy ra P(G) = $\frac{n\left(G\right)}{n\left(\Omega \right)}=\frac{4}{16}=\frac{1}{4}$ .

Gọi biến cố K: “Một quán có 3 bạn vào, quán kia có 1 bạn vào.”. Ta có:

K₁: “Quán A có 3 bạn vào, quán B có 1 bạn vào” nên K₁ = G, n(K₁) = 4.

K₂: “Quán B có 3 bạn vào, quán A có 1 bạn vào”. Ta có:

K₂ = {BBBA; BBAB; BABB; ABBB}, n(K₂) = 4

n(K) = n(K₁) + n(K₂) = 4 + 4 = 8.

Vậy P(K) = $\frac{n\left(K\right)}{n\left(\Omega \right)}=\frac{8}{16}=\frac{1}{2}$ .

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 25: Nhị thức Newton

Bài tập cuối chương 8

Bài 26: Biến cố và định nghĩa cổ điển của xác suất

Bài tập cuối chương 9