Với lời giải SBT Toán 10 trang 46 Tập 2 chi tiết trong Bài 22: Ba đường conic sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 22: Ba đường conic

Bài 7.28 trang 46 SBT Toán 10 Tập 2: Cho elip (E) có phương trình $\frac{x^2}{36}+\frac{y^2}{16}=1$ . Tìm tiêu điểm và tiêu cự của elip.

Lời giải:

Dựa vào phương trình chính tắc $\frac{x^2}{36}+\frac{y^2}{16}=1$  của (E) ta có

$\left\{\begin{array}{c}{a}^2=36\\ b^2=16\end{array}\right.\Rightarrow c=\sqrt{a^2-b^2}=2\sqrt{5}$

Vậy (E) có hai tiêu điểm là: $F_1\left(-2\sqrt{5};0\right),F_2\left(2\sqrt{5};0\right)$ và có tiêu cự là: $2c=4\sqrt{5}$ .

Bài 7.29 trang 46 SBT Toán 10 Tập 2: Cho hypebol (H) có phương trình $\frac{x^2}{16}-\frac{y^2}{20}=1$. Tìm tiêu điểm và tiêu cự của hypebol.

Lời giải:

Dựa vào phương trình chính tắc $\frac{x^2}{16}-\frac{y^2}{20}=1$  của (H) ta có

$\left\{\begin{array}{c}{a}^2=16\\ b^2=20\end{array}\right.\Rightarrow c=\sqrt{a^2+b^2}=6$

Vậy (H) có hai tiêu điểm là F₁ (–6; 0), F₂(6; 0) và có tiêu cự là 2c = 12.

Bài 7.30 trang 46 SBT Toán 10 Tập 2: Cho parabol (P) có phương trình y² = 4x. Tìm tiêu điểm và đường chuẩn của parabol.

Lời giải:

Dựa vào phương trình chính tắc y² = 4x của (P) ta có:

2p = 4 ⇔ p = 2 ⇔ $\frac{p}{2}=1$  .

Vậy (P) có tiêu điểm là F(1; 0) và có đường chuẩn là Δ: x = –1.

Bài 7.31 trang 46 SBT Toán 10 Tập 2: Viết phương trình chính tắc của elip (E), biết (E) đi qua điểm A(6; 0) và có tiêu cự bằng 8.

Lời giải:

Phương trình chính tắc của (E) có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$  (trong đó a > b > 0)

Vì (E) đi qua điểm A(6; 0) nên ta có $\frac{6^2}{a^2}+\frac{0^2}{b^2}=1$  ⇔ a² = 6² 

Do (E) có tiêu cự là 2c = 8 nên ta có c = 4 ⇒ b² = a² – c² = 6² – 4² = 20.

Vậy phương trình chính tắc của (E) là: $\frac{x^2}{36}+\frac{y^2}{20}=1$ .

Bài 7.32 trang 46 SBT Toán 10 Tập 2: Viết phương trình chính tắc của hypebol (H), biết (H) đi qua điểm $M\left(3\sqrt{2};-4\right)$ và có một tiêu điểm là F₂(5; 0).

Lời giải:

Phương trình chính tắc của (H) có dạng: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$   (trong đó a, b > 0)

Do (H) có một tiêu điểm là F₂(5; 0) nên ta có:

c = 5 ⇒ b² + a² = c² = 25 ⇔ a² = 25 – b²

Vì (H) đi qua điểm $M\left(3\sqrt{2};4\right)$ nên ta có

$\frac{{\left(3\sqrt{2}\right)}^2}{a^2}-\frac{4^2}{b^2}=1\iff \frac{18}{a^2}-\frac{16}{b^2}=1$            (1)

Đặt t = b² (t > 0) ⇒ a² = 25 – t. Thay vào (1) ta được

$\frac{18}{25-t}-\frac{16}{t}=1$

⇒ 18t – 16(25 – t) = (25 – t)t

⇔ 18t – 400 + 16t = 25t – t²

⇔ t² + 9t – 400 = 0

⇔ t = 16 (thỏa mãn) hoặc t = –25 (không thỏa mãn)

Do đó, b² = t = 16, a² = 25 – t = 9.

Vậy phương trình chính tắc của (H) là: $\frac{x^2}{9}-\frac{y^2}{16}=1$ .

Bài 7.33 trang 46 SBT Toán 10 Tập 2: Viết phương trình chính tắc của parabol (P), biết rằng (P) có đường chuẩn là đường thẳng Δ: x + 4 = 0. Tìm toạ độ điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của (P) bằng 5.

Lời giải:

Phương trình chính tắc của (P) có dạng y² = 2px, trong đó p > 0.

Vì (P) có đường chuẩn là Δ: x + 4 = 0 ⇔ x = –4 ⇔ –p : 2 = –4 ⇔ p = 8

Vậy phương trình chính tắc của (P) là y² = 16x.

Gọi M (x₀; y₀).

Vì M thuộc (P) nên ta có:

d(M, Δ) = MF = 5 với F là tiêu điểm của (P) và F(4; 0).

$\iff \frac{\left|x_0+4\right|}{\sqrt{1^2+0^2}}=5$

⇔ |x₀ + 4| = 5 (*)

TH1: x₀ + 4 ≥ 0 hay x₀ ≥ –4

 (*) ⇔  x₀ + 4 = 5  ⇔ x₀ = 1 (thỏa mãn)

TH2: x₀ + 4 < 0 hay x₀ < –4

 (*) ⇔  –x₀ – 4 = 5  ⇔ x₀ = –9 (thỏa mãn)

Với x₀ = –9, thay vào phương trình của (P) ta được y₀² = 16.(–9) = –144 < 0 (không thể tồn tại)

Với x₀ = 1, thay vào phương trình của (P) ta được y₀² = 16.1 = 16 ⇔ y₀  = ±4

Vậy M(1; 4) hoặc M(1; –4).

Bài 7.34 trang 46 SBT Toán 10 Tập 2: Cho parabol (P) có phương trình là y² = 16x. Gọi Δ là đường thẳng bất kì đi qua tiêu điểm F của (P) và không trùng với trục hoành. Chứng minh rằng Δ luôn cắt (P) tại hai điểm phân biệt A, B, đồng thời tích các khoảng cách từ A và B đến trục hoành không đổi.

Lời giải:

Gọi vectơ chỉ phương của Δ là $\overrightarrow{u_{\Delta }}=\left(a;b\right)$ . Vì Δ đi qua điểm F(4; 0) và Δ không trùng với trục Ox nên ta có b ≠ 0. Phương trình tham số của Δ là

$\left\{\begin{array}{c}x=4+at\\ y=0+bt=bt\end{array}\right.$.

Toạ độ giao điểm của Δ và (P) ứng với thoả mãn phương trình

(bt)² =16 . (4 + at) ⇔ b²t² – 16at – 64 = 0. (1)

Phương trình (1) có Δ’ = 64a² + 64b² > 0 (do b ≠ 0), suy ra phương trình (1) luôn có 2 nghiệm phân biệt. Vậy Δ luôn cắt (P) tại hai điểm phân biệt A, B.

Gọi A(4 + at₁; bt₁), B(4 + at₂; bt₂), trong đó t₁, t₂ là hai nghiệm của phương trình (1).

Ta có

$d\left(A,Ox\right).d\left(B,Ox\right)=\frac{\left|b{t}_1\right|}{\sqrt{0^2+1^2}}.\frac{\left|b{t}_2\right|}{\sqrt{0^2+1^2}}=\left|b^2.t_1{t}_2\right|$

Dựa vào phương trình (1). Theo định lí Vi–ét ta có: $t_1{t}_2=\frac{-64}{b^2}$ . Từ đó suy ra

$d\left(A,Ox\right).d\left(B,Ox\right)=\left|b^2.\frac{-64}{b^2}\right|=64$

Vậy tích các khoảng cách từ A và B đến trục hoành không đổi.

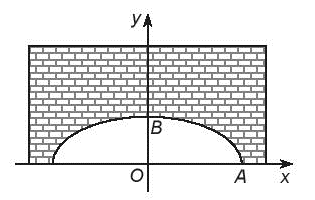
 Bài 7.35 trang 46 SBT Toán 10 Tập 2: Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hầm là 12 m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8 m thì có chiều rộng không quá 3 m. Hỏi chiếc xe tải có chiều cao 2,8 m có thể đi qua hầm được không?

Lời giải:

Giả sử phương trình chính tắc của (E) là: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$  (trong đó a > b > 0).

Vì chiều rộng của hầm là 12 m nên OA = 12 : 2 = 6 (m), do đó điểm A có tọa độ (6; 0).

Khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m nên OB = 3 m, do đó điểm B có tọa độ (0; 3).

Do các điểm B(0; 3) và A(6; 0) thuộc (E) nên thay vào phương trình của (E) ta có:

$$\begin{gathered} \frac{0^2}{a^2}+\frac{3^2}{b^2}=1\Rightarrow b^2=3^2=9 \\ \frac{6^2}{a^2}+\frac{0^2}{b^2}=1\Rightarrow a^2=6^2=36 \end{gathered}$$

Suy ra phương trình của (E) là

$\frac{x^2}{36}+\frac{y^2}{9}=1$.

Với những xe tải có chiều cao 2,8 m, chiều rộng của xe tải là 3 m, nếu xe chạy chính giữa hầm thì khoảng cách từ tâm xe tới mỗi bên xe khoảng 3 : 2 = 1,5 m, tương ứng với x = 1,5. Thay vào phương trình của elip để ta tìm ra độ cao y của điểm M (có hoành độ bằng 1,5 thuộc (E)) so với trục Ox.

$\frac{{x_M}^2}{36}+\frac{{y_M}^2}{9}=1$

Suy ra: $y_M=3.\sqrt{1-\frac{x_M^2}{36}}=3.\sqrt{1-\frac{{\mathrm{1,5}}^2}{36}}\approx \mathrm{2,905}>\mathrm{2,8}$

Kết luận: Ô tô tải có thể đi được qua hầm, tuy nhiên cần khuyến cáo ô tô phải đi vào chính giữa hầm.

Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 10 trang 47 Tập 2

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 22: Ba đường conic

Bài tập cuối chương 7

Bài 23: Quy tắc đếm

Bài 24: Hoán vị, chỉnh hợp và tổ hợp