Với lời giải SBT Toán 10 trang 21 Tập 2 chi tiết trong Bài 18: Phương trình quy về phương trình bậc hai sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 18: Phương trình quy về phương trình bậc hai
Bài 6.28 trang 21 SBT Toán 10 Tập 2: Giải các phương trình sau:
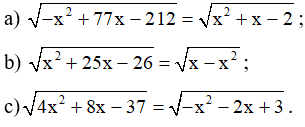
Lời giải:
a)
(1)
Bình phương hai vế của (1) ta có:
–x2 + 77x – 212 = x2 + x – 2
⇔ 2x2 – 76x + 210 = 0
⇔ x = 35 hoặc x = 3
Thay x = 35 vào (1) ta có:
Thay x = 3 vào (1) ta có:
Vậy tập nghiệm của phương trình (1) là S = {3; 35}.
b)
(2)
Bình phương hai vế của (2) ta có:
x2 + 25x – 26 = x – x2
⇔ 2x2 + 24x – 26 = 0
⇔ x = 1 hoặc x = –13
Thay x = 1 vào (2) ta có:
⇔ 0 = 0 (thỏa mãn)
Thay x = –13 vào (2) ta có:
(không thể tồn tại)
Vậy tập nghiệm của phương trình (2) là S = {1}.
c)
(3)
Bình phương hai vế của (3) ta có:
4x2 + 8x – 37 = –x2 – 2x + 3
⇔ 5x2 + 10x – 40 = 0
⇔ x = 2 hoặc x = –4
Thay x = 2 vào (3) ta có:
(không thể tồn tại)
Thay x = –4 vào (3) ta có:
(không thể tồn tại)
Vậy tập nghiệm của phương trình (3) là S = ∅.
Bài 6.29 trang 21 SBT Toán 10 Tập 2: Giải các phương trình sau:
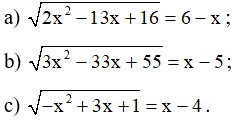
Lời giải:
a)
(1)
Bình phương hai vế của (1) ta có:
2x2 – 13x + 16 = (6 – x)2
⇔ 2x2 – 13x + 16 = 36 – 12x + x2
⇔ x2 – x – 20 = 0
⇔ x = 5 hoặc x = –4
Thay x = 5 vào (1) ta có:
(thỏa mãn)
Thay x = –4 vào (1) ta có:
Vậy tập nghiệm của phương trình (1) là S = {–4; 5}.
b)
(2)
Bình phương hai vế của (2) ta có:
3x2 – 33x + 55 = (x – 5)2
⇔ 3x2 – 33x + 55 = x2 – 10x + 25
⇔ 2x2 – 23x + 30 = 0
⇔ x = 10 hoặc x = 1,5
Thay x = 10 vào (2) ta có:
(thỏa mãn)
Thay x = 1,5 vào (2) ta có:
(không thỏa mãn)
Vậy tập nghiệm của phương trình (2) là S = {10}.
c)
(3)
Bình phương hai vế của (3) ta có:
–x2 + 3x + 1 = (x – 4)2
⇔ –x2 + 3x + 1 = x2 – 8x + 16
⇔ 2x2 – 11x + 15 = 0
⇔ x = 3 hoặc x = 2,5
Thay x = 3 vào (3) có:
(không thỏa mãn)
Thay x = 2,5 vào (3) có:
(không thỏa mãn)
Vậy phương trình (3) có tập nghiệm là S = ∅.
Bài 6.30 trang 21 SBT Toán 10 Tập 2: Giải các phương trình sau:
a) ;
b) .
Lời giải:
a)
(1)
Bình phương hai vế của (1) ta có:
2x – 3 = (x – 3)2
⇔ 2x – 3 = x2 – 6x + 9
⇔ x2 – 8x + 12 = 0
⇔ x = 6 hoặc x = 2
Thay x = 6 vào (1) ta có:
(thỏa mãn)
Thay x = 2 vào (1) ta có:
(không thỏa mãn)
Vậy tập nghiệm của phương trình là: S = {6}.
b)
Do x2 + 4 > 0 với mọi số thực x nên luôn có nghĩa với mọi số thực x
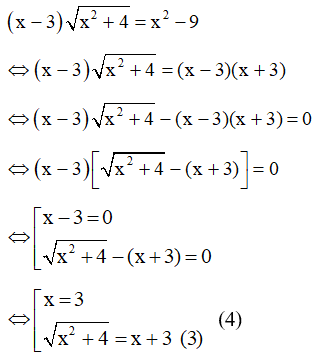
Bình phương hai vế của phương trình (3) ta có:
x2 + 4 = (x + 3)2
⇔ x2 + 4 = x2 + 6x + 9
⇔ 6x = –5
⇔
Thay vào (3) ta có:
(thỏa mãn)
Phương trình (3) có nghiệm là: .
Do đó, (4)
Vậy tập nghiệm của phương trình đã cho là S = .
Bài 6.31 trang 21 SBT Toán 10 Tập 2: Tìm điều kiện của tham số m để phương trình sau có nghiệm: .
Lời giải:
(1)
Bình phương hai vế của (1) ta có:
2x2 + x + 1 = x2 + mx + m – 1
⇔ x2 + (1 – m)x + 2 – m = 0 (2)
Xét tam thức bậc hai f(x) = 2x2 + x + 1 có: a = 2 > 0, ∆f = 12 – 4.2.1 = –7 < 0
Do đó, f(x) = 2x2 + x + 1 > 0 với mọi số thực x nên x2 + mx + m – 1 > 0 với mọi số thực x, do đó, , luôn có nghĩa với mọi số thực x.
Do đó, (1) có nghiệm khi và chỉ khi (2) có nghiệm.
Xét phương trình bậc hai (2) ta có:
∆ = (1 – m)2 – 4.1.(2 – m) = 1 – 2m + m2 – 8 + 4m = m2 + 2m – 7
Phương trình (2) có nghiệm khi và chỉ chi ∆ ≥ 0
⇔ m2 + 2m – 7 ≥ 0
Xét phương trình bậc hai ẩn m là: m2 + 2m – 7 = 0 có:
a = 1 > 0
∆m = 22 – 4.1.(–7) = 32 > 0
Do đó, phương trình có hai nghiệm phân biệt là:
Do đó, m2 + 2m – 7 ≥ 0 ⟺
Vậy khi hoặc thì phương trình có nghiệm.
Bài 6.32 trang 21 SBT Toán 10 Tập 2: Mặt cắt đứng của cột cây số trên quốc lộ có dạng nửa hình tròn ở phía trên và phía dưới có dạng hình chữ nhật (xem hình dưới). Biết rằng đường kính của nửa hình tròn cũng là cạnh phía trên của hình chữ nhật và đường chéo của hình chữ nhật có độ dài 66 cm. Tìm kích thước của hình chữ nhật, biết rằng diện tích của phần nửa hình tròn bằng 0,3 lần diện tích của phần hình chữ nhật. Lấy π = 3,14 và làm tròn kết quả đến chữ số thập phân thứ hai.
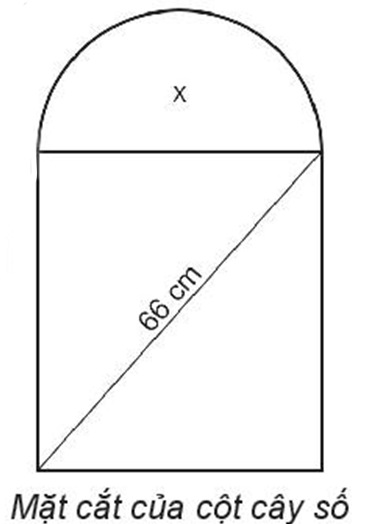
Lời giải:
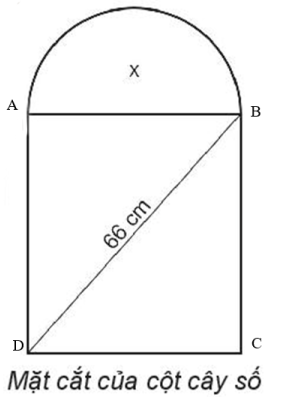
Gọi đường kính của nửa hình tròn là x (cm) (x > 0).
Độ dài cạnh phía trên của hình chữ nhật bằng đường kính của nửa hình tròn hay AB = x (cm).
Xét tam giác vuông ABD
Áp dụng định lí Pythagore, ta có:
BD2 = AD2 + AB2
⇔ AD2 = BD2 – AB2
Suy ra
.
Độ dài cạnh còn lại của hình chữ nhật là AD =
Diện tích nửa hình tròn là .
Diện tích hình chữ nhật là x. Theo giả thiết ta có:
(do x > 0).
Bình phương hai vế của phương trình ta có:
24 649x2 = 14 400(4 356 – x2)
⇔ 24 649x2 = 62 726 400 – 14 400x2
⇔ 39 049x2 = 62 726 400
⇔ x ≈ ± 40,08
Do x > 0 nên ta có: x = 40,08
Độ dài cạnh trên của hình chữ nhật là 40,08 cm, độ dài cạnh còn lại là: (cm)
Vậy kích thước của hình chữ nhật khoảng 40,08 cm × 52,44 cm.
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 17: Dấu của tam thức bậc hai
Bài 18: Phương trình quy về phương trình bậc hai
Bài 19: Phương trình đường thẳng
Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách