Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 1: Hình hộp chữ nhật hay, chi tiết giúp học sinh dễ dàng làm bài tập Hình hộp chữ nhật lớp 8.

Giải bài tập Toán lớp 8 Bài 1: Hình hộp chữ nhật

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 96 Toán 8 Tập 2: Quan sát hình hộp chữ nhật ABCD.A'B'C'D' (h.71a). Hãy kể tên các mặt, các đỉnh và các cạnh của hình hộp chữ nhật.

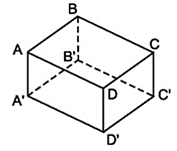
Lời giải:

- Các mặt: ABCD, A'B'C'D', ABB'A', CDD'C', ADD'A', BCC'B'

- Các đỉnh: A, B, C, D, A', B', C', D'

- Các cạnh: AB, BC, CD, DA, A'B', B'C', C'D', D'A', AA', BB', CC', DD'.

Bài tập (trang 96; 97)

Bài 1 trang 96 Toán 8 Tập 2: Hãy kể tên những cạnh bằng nhau của hình hộp chữ nhật ABCD.MNPQ (h.72).

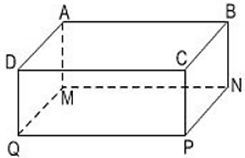
Hình 72

Lời giải:

Trong hình hộp chữ nhật ABCD.MNPQ những cạnh bằng nhau là:

AB = CD = PQ = MN

AD = QM = PN = CB

DQ = AM = BN = CP

Bài 2 trang 96 Toán 8 Tập 2: ABCD.A₁B₁C₁D₁ là một hình hộp chữ nhật (h.73).

a) Nếu O là trung điểm của đoạn CB₁ thì O có là điểm thuộc đoạn BC₁ hay không?

b) K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh BB₁ hay không?

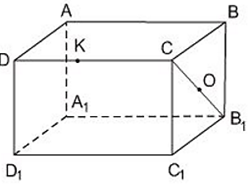
Hình 73

Lời giải:

Với hình hộp chữ nhật ABCD.A₁B₁C₁D₁:

a) Nếu O là trung điểm của đoạn CB₁ thì O cũng là trung điểm của đoạn C₁B vì CBB₁C₁ là hình chữ nhật nên hai đường chéo cắt nhau tại trung điểm mỗi đường (tính chất hình chữ nhật).

b) K là điểm thuộc cạnh CD thì K không thuộc cạnh BB₁ vì bốn điểm C, D, B, B₁ không thuộc một mặt phẳng.

Bài 3 trang 97 Toán 8 Tập 2: Các kích thước của hình hộp chữ nhật ABCD.A₁B₁C₁D₁ là DC = 5cm, CB = 4cm, BB₁ = 3cm. Hỏi độ dài DC₁ và CB₁ là bao nhiêu xentimet?

Lời giải:

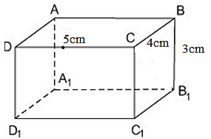
Vì ABCD.A₁B₁C₁D₁ là hình hộp chữ nhật

⇒ DCC₁D₁ và CBB₁C₁ là hình chữ nhật.

⇒ CC₁ = BB₁ = 3cm

ΔDCC₁ vuông tại C, áp dụng định lí Py-ta–go ta có:

DC₁² = DC² + CC₁²

$D{C}_1=\sqrt{D{C}^2+\text{\hspace{0.17em}\hspace{0.17em}}C{C}_1^2}$= $\sqrt{5^2+3^2}$

$=\sqrt{25+9}=\sqrt{34}\approx 5,83cm$

ΔCBB₁ vuông tại B, áp dụng định lí Py–ta-go ta có:

CB₁²= CB² + BB₁²

$C{B}_1=\sqrt{C{B}^2+\text{\hspace{0.17em}\hspace{0.17em}}B{B}_1^2}$= $\sqrt{4^2+3^2}$

$=\sqrt{16+9}=\sqrt{25}=5cm$.

Bài 4 trang 97 Toán 8 Tập 2: Xem hình 74a, các mũi tên hướng dẫn cách ghép các cạnh với nhau để có được một hình lập phương.

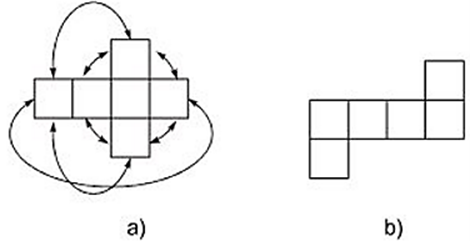
Hình 74

Hãy điền thêm vào hình 74b các mũi tên như vậy.

Lời giải:

Mỗi hình vuông tương ứng với một mặt của hình lập phương có 6 mặt. Đầu tiên chúng ta giữ cố định một hình vuông ở giữa để làm một mặt trong cùng của hình lập phương, sau đó di chuyển các hình vuông còn lại theo chiều mũi tên như sau để được hình lập phương: