Hình hộp chữ nhật - Hình học toán 8

Tưởng Thị Hồng Vân Ngày: 08-03-2024 Lớp 8

Tải xuống 10 3.6 K 10

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập về Hình hộp chữ nhật Toán lớp 8, tài liệu bao gồm 10 trang, tuyển chọn các bài tập Hình hộp chữ nhật có đầy đủ lý thuyết và phương pháp giải chi tiết và bài tập có lời giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Hình hộp chữ nhật gồm các nội dung chính sau:

I. Phương pháp giải

- tóm tắt lý thuyết ngắn gọn;

- phương pháp giải chi tiết từng dạng bài tập.

II. Một số ví dụ/ Ví dụ minh họa

- gồm 5 ví dụ minh họa đa dạng của các dạng bài tập trên có lời giải chi tiết.

III. Bài tập vận dụng

- gồm 11 bài tập vận dụng (11 bài tập có đáp án và lời giải chi tiết) giúp học sinh tự rèn luyện cách giải các dạng bài tập Hình hộp chữ nhật.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây: Hình hộp chữ nhật - Hình học toán 8 (ảnh 1)

Hình hộp chữ nhật

I. Phương pháp giải

1. Hình hộp chữ nhật

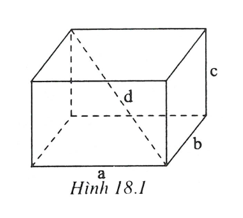
- Hình 18.1 cho ta hình ảnh của một hình hộp chữ nhật.

- Hình hộp chữ nhật có 6 mặt, 8 đỉnh và 12 cạnh.

- Hình lập phương có 6 mặt là những hình vuông.

2. Diện tích xung quanh và thể tích của hình hộp chữ nhật

· Diện tích xung quanh của hình hộp chữ nhật bằng chu vi đáy nhân với chiều cao.

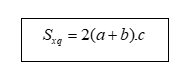
Hình hộp chữ nhật - Hình học toán 8 (ảnh 3)

· Diện tích toàn phần của hình hộp chữ nhật bằng tổng của diện tích xung quanh và diện tích hai đáy.

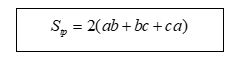
Hình hộp chữ nhật - Hình học toán 8 (ảnh 4)

Thể tích của hình hộp chữ nhật bằng tích của ba kích thước.

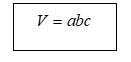
Hình hộp chữ nhật - Hình học toán 8 (ảnh 5)

Đặc biệt, đối với hình lập phương thì:

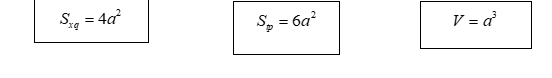Hình hộp chữ nhật - Hình học toán 8 (ảnh 6) 3. Tính chất đường chéo của hình hộp chữ nhật

· Bốn đường chéo của hình hộp chữ nhật cắt nhau tại trung điểm của mỗi đường.

· Bình phương của mỗi đường chéo bằng tổng các bình phương của ba kích thước.

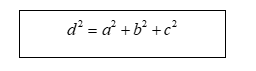
4. Quan hệ vị trí của hai đường thẳng phân biệt trong không gian (h.18.2)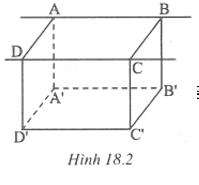 Hình hộp chữ nhật - Hình học toán 8 (ảnh 8)

· Cắt nhau: Nếu hai đường thẳng có một điểm chung.

Ví dụ: AB và BC.

· Song song: Nếu hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.

Ví dụ: AB và CD.

· Chéo nhau: Nếu hai đường thẳng không cùng nằm trong một mặt phẳng nào.

Ví dụ: AB và $C C^{'}$

Nhận xét. Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song.

5. Quan hệ song song của đường thẳng và mặt phẳng (h.18.2)

· Đường thẳng song song với mặt phẳng khi chúng không có điểm chung.

Ví dụ: $A B // m p (A^{'} B^{'} C^{'} D^{'})$ .

· Nếu $A B ⊄ m p (P); A^{'} B^{'} \subset m p (P)$ và $A B // A^{'} B^{'}$ thì $A B ∥ // m p (P)$ .

Nhận xét. Nếu thì đường thẳng AB nằm trọn trong mp(P)

Xem thêm

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10

Tài liệu có 10 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

toán 8 Hình hộp chữ nhật

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm