Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Ôn tập chương 2 Hình học hay, chi tiết giúp học sinh dễ dàng làm bài tập Ôn tập chương 2 Hình học lớp 8.

Giải bài tập Toán lớp 8 Ôn tập chương 2 Hình học

Trả lời câu hỏi giữa bài

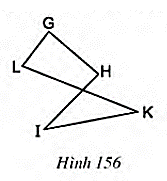
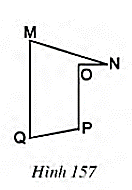
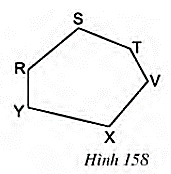
Câu hỏi 1 trang 131 Toán 8 Tập 1: Xem các hình 156, 157, 158 và trả lời các câu hỏi sau:

a) Vì sao hình năm cạnh GHIKL (h.156) không phải là đa giác lồi?

b) Vì sao hình năm cạnh MNOPQ (h.157) không phải là đa giác lồi?

c) Vì sao hình sáu cạnh RSTVXY (h.158) là một đa giác lồi?

Hãy phát biểu định nghĩa đa giác lồi.

Trả lời:

a) Đa giác GHIKL nằm ở hai nửa mặt phẳng có bờ là đường thẳng IH (hoặc bờ LK) nên đa giác GHIKL không là đa giác lồi.

b) Đa giác MNOPQ không phải là đa giác lồi vì đa giác nằm trong hai nửa mặt phẳng có bờ là đường thẳng NO (hoặc bờ PO).

c) Đa giác RSTVXY là đa giác lồi vì luôn nằm trong cùng nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.

Câu hỏi 2 trang 132 Toán 8 Tập 1:Điền vào chỗ trống trong các câu sau:

a) Biết rằng tổng số đo các góc của một đa giác n cạnh là $\widehat{A_1}+\widehat{A_2}+\mathrm{...}+\widehat{A_n}=\left(n-2\right){.180}^o.$

Vậy tổng số đo các góc của một đa giác 7 cạnh là ….

b) Đa giác đều là đa giác có ….

c) Biết rằng số đo mỗi góc của một đa giác đều n cạnh là $\frac{\left(n-2\right){.180}^0}{n}$. Vậy:

Số đo mỗi góc của ngũ giác đều là ....

Số đo mỗi góc của lục giác đều là ....

Lời giải

Ta điền vào chỗ trống như sau:

a) Vậy tổng số góc của đa giác 7 cạnh là:

(7 - 2).180^o = 900^o.

b) Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

c) Số đo mỗi góc của ngũ giác đều là $\frac{\left(5-2\right){.180}^0}{5}=\frac{{3.180}^o}{5}={108}^o$.

Số đo mỗi góc của lục giác đều là $\frac{\left(6-2\right){.180}^0}{6}=\frac{{4.180}^o}{6}={120}^o$.

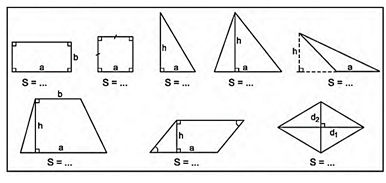
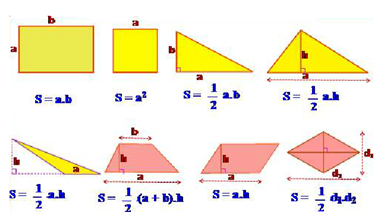
Câu hỏi 3 trang 132 Toán 8 Tập 1:Hãy viết công thức tính diện tích của mỗi hình trong khung sau:

Lời giải

Theo thứ tự từ trái sang phải, ta có:

Hình 1 là hình chữ nhật nên S = ab;

Hình 2 là hình vuông nên S = a²;

Hình 3 là tam giác vuông với đáy là a và chiều cao tương ứng là b: $S=\frac{1}{2}ab;$

Hình 4 là tam giác với đáy là a và chiều cao tương ứng là h: $S=\frac{1}{2}ah;$

Hình 5 là tam giác với đáy là a và chiều cao tương ứng là h: $S=\frac{1}{2}ah;$

Hình 6 là hình thang với độ dài hai đáy là a và b, chiều cao là h: $S=\frac{\left(a+b\right)h}{2};$

Hình 7 là hình bình hành với đáy là a và chiều cao tương ứng là h: S = a.h;

Hình 8 là hình thoi có độ dài hai đường chéo là d₁ và d₂: $S=\frac{1}{2}{d}_1.d_2.$

Tương ứng ta có bảng sau:

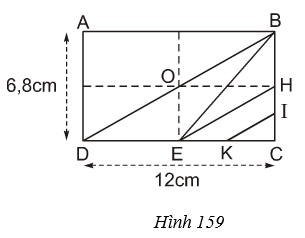
Bài tập (trang 132; 133)

Bài 41 trang 132 Toán 8 Tập 1:Cho hình chữ nhật ABCD. Gọi H, I, E, K lần lượt là các trung điểm của BC, HC, DC, EC (h.159). Tính

a) Diện tích tam giác DBE

b) Diện tích tứ giác EHIK

Lời giải:

Vì ABCD là hình chữ nhật nên AD = BC = 6,8 cm.

Ta có: DE = EC = $\frac{DC}{2}=\frac{12}{2}=6cm$ (Vì E là trung điểm của DC).

EK = KC = $\frac{EC}{2}=\frac{6}{2}=3cm$ (Vì K là trung điểm của EC)

Ta lại có: BH = HC = $\frac{BC}{2}=\frac{6,8}{2}=3,4cm$ (Vì H là trung điểm của BC).

HI = IC = $\frac{HC}{2}=\frac{3,4}{2}=1,7cm$ (Vì I là trung điểm HC)

a) Diện tích tam giác DBE là: 

$S_{DBE}=\frac{1}{2}DE.BC=\frac{1}{2}\mathrm{.6.6.8}=20,4\left(c{m}^2\right).$

Vậy diện tích tam giác DBE là 20,4 cm².

b) Diện tích EBC bằng diện tích tam giác DBE bằng 20,4 cm² vì DE = EC và chung chiều cao BC.

Diện tích tam giác EBH là: 

$S=\frac{1}{2}.BH.EC=\frac{1}{2}.3,4.6=10,2\left(c{m}^2\right).$

Diện tích tam giác KCI là:

$S=\frac{1}{2}.KC.IC=\frac{1}{2}.1,7.3=2,55\left(c{m}^2\right).$

Ta có:

$$\begin{gathered} S_{EHIK}=S_{EBC}-S_{EBH}-S_{KIC} \\ =20,4-5,1-2,55=12,75\left(c{m}^2\right). \end{gathered}$$

Vậy diện tích tứ giác EHIK là 12,75 cm².

Bài 42 trang 132 Toán 8 Tập 1: Trên hình 160 (AC // BF), hãy tìm tam giác có diện tích bằng diện tích tứ giác ABCD.

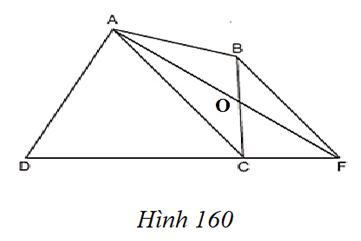
Lời giải:

Ta có: BF// AC

⇒ Khoảng cách từ B đến AC bằng khoảng cách từ F đến AC.

⇒ S_BAC = S_FAC (Chung đáy AC, chiều cao bằng nhau).

⇒ S_ABC + S_ADC = S_FAC + S_ADC

hay S_ABCD = S_ADF.

Vậy tam giác ADF có diện tích bằng diện tích tứ giác ABCD.

Bài 43 trang 133 Toán 8 Tập 1: Cho hình vuông ABCD có tâm đối xứng O, cạnh a. Một góc vuông xOy có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F (h.161). Tính diện tích tứ giác OEBF.

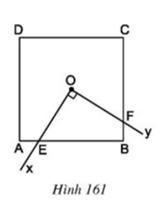
Lời giải:

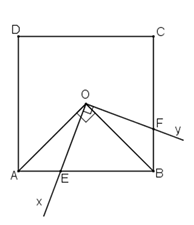
Ta có $\widehat{OAE}=\frac{\widehat{DAB}}{2}=\frac{{90}^0}{2}={45}^0$ (AO là phân giác )

$\widehat{OBF}=\frac{\widehat{ABC}}{2}=\frac{{90}^0}{2}={45}^0$ (BO là phân giác )

$\Rightarrow \widehat{OAE}=\widehat{OBF}=45°$.

Ta lại có $\widehat{AOE}+\widehat{EOB}={90}^0$ (hai góc phụ nhau)

$\widehat{BOF}+\widehat{EOB}={90}^0$(hai góc phụ nhau)

$\Rightarrow \widehat{AOE}=\widehat{BOF}=90°-\widehat{EOB}$.

Xét $\Delta OAE$ và $\Delta OBF$, có:

$\widehat{AOE}=\widehat{BOF}\left(cmt\right)$

OA = OB (tính chất hình vuông)

$\begin{array}{l}\widehat{OAE}=\widehat{OBF}\left(cmt\right)\\ \Rightarrow \Delta OAE=\Delta OBF\left(g-c-g\right)\\ \Rightarrow S_{\Delta OAE}=S_{\Delta OBF}\end{array}$

Mà $S_{\Delta OAE}+S_{\Delta OBE}=S_{\Delta AOB}$ và $S_{\Delta OFB}+S_{\Delta OBE}=S_{OEBF}$

$\Rightarrow S_{\Delta AOB}=S_{OEBF}$

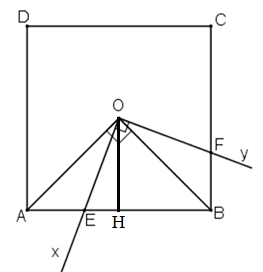
Kẻ OH vuông góc AB nên $OH=\frac{AB}{2}=\frac{a}{2}$

Diện tích tam giác vuông AOB là: $S_{AOB}=\frac{1}{2}OH.AB=\frac{1}{2}.\frac{a}{2}.a=\frac{a^2}{4}$.

Vậy diện tích tứ giác OEBF là $\frac{a^2}{4}.$

Bài 44 trang 133 Toán 8 Tập 1:Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO.

Lời giải:

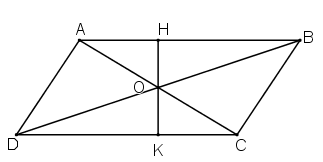
Gọi OH, OK lần lượt là chiều cao của tam giác AOB và tam giác DOC.

Ta có: OK ⊥ CD, CD // AB ⇒ OK ⊥ AB

⇒ O, H, K thẳng hàng.

Do đó:

$\begin{array}{l}{S}_{AOB}+S_{COD}=\frac{1}{2}AB.OH+\frac{1}{2}CD.OK\\ =\frac{1}{2}AB.OH+\frac{1}{2}AB.OK\\ =\frac{1}{2}AB.\left(OH+OK\right)\\ =\frac{1}{2}AB.HK=\frac{1}{2}{S}_{ABCD}\end{array}$

Mà S_ABCD = S_AOB + S_BOC + S_COD + S_DOA

_{$$\begin{gathered} \Rightarrow S_{AOC}+S_{BOD}=S_{ABCD}-S_{AOB}-S_{COD} \\ =S_{ABCD}-\frac{1}{2}{S}_{ABCD}=\frac{1}{2}{S}_{ABCD} \end{gathered}$$}

$\Rightarrow S_{AOC}+S_{BOD}=S_{AOB}+S_{COD}$

Vậy S_AOB + S_COD = S_BOC + S_DOA.

Bài 45 trang 133 Toán 8 Tập 1:Hai cạnh của một hình bình hành có độ dài là 6cm và 4cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao kia.

Lời giải:

Gọi đường cao còn lại là h.

Theo quan hệ giữa đường xiên và hình chiếu thì ta có chiều cao của hình bình hành luôn nhỏ hơn cạnh không tương ứng với nó.

⇒ Đường cao có độ dài bằng 5cm ứng với cạnh 4cm

⇒ S_ABCD = 4.5 = 20

Mà S_ABCD = h.6

⇒ h.6 = 20

⇒ h = 20 : 6 = 3,33 (cm).

Bài 46 trang 133 Toán 8 Tập 1:Cho tam giác ABC. Gọi M, N là các trung điểm tương ứng của AC, BC. Chứng minh rằng diện tích của hình thang ABNM bằng $\frac{3}{4}$ diện tích của tam giác ABC.

Lời giải:

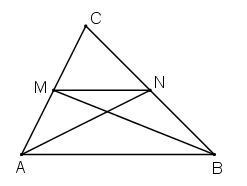
Vẽ hai trung tuyến AN, BM của ΔABC. Ta có:

N là trung điểm BC ⇒ $S_{ACN}=\frac{1}{2}{S}_{ABC}$ (chung chiều cao từ A, đáy CN = $\frac{1}{2}$.BC)

M là trung điểm CA ⇒ $S_{MCN}=\frac{1}{2}{S}_{ACN}$ (chung chiều cao từ N, đáy CM = $\frac{1}{2}$CA).

$\Rightarrow S_{MCN}=\frac{1}{2}{S}_{ACN}=\frac{1}{2}.\frac{1}{2}.S_{ABC}$

$$\begin{gathered} \Rightarrow S_{ABNM}=S_{ABC}-S_{CMN} \\ =S_{ABC}-\frac{1}{4}{S}_{ABC} \end{gathered}$$

$=\frac{3}{4}{S}_{ABC}$ (đpcm).

Bài 47 trang 133 Toán 8 Tập 1:Vẽ ba đường trung tuyến của một tam giác (h.162). Chứng minh sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau.

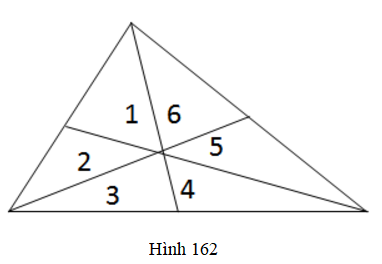
Lời giải:

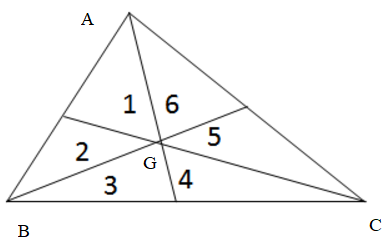
Theo tính chất trung tuyến, suy ra:

S₁ = S₂ (có đáy bằng nhau và cùng chiều cao kẻ từ G xuống cạnh AB) (1)

S₃ = S₄ (có đáy bằng nhau và cùng chiều cao kẻ G xuống cạnh BC) (2)

S₅ = S₆ (có đáy bằng nhau và cùng chiều cao kẻ từ G xuống AC) (3)

Ta có:

S₁ + S₂ + S₃ = S₄ + S₅ + S₆ $\left(=\frac{S_{ABC}}{2}\right)$.

⇔ 2S₁ + S₃= S₄ + 2S₆ (vì S₁ = S₂; S₅ = S₆)

⇔ 2S₁ = 2S₆ (vì S₃ = S₄)

⇔ S₁ = S₆ (4)

Và S₁+ S₂ + S₆ = S₃ + S₄ +S₅ $\left(=\frac{S_{ABC}}{2}\right)$ (5)

Kết hợp (5) với (1), (2), (3) suy ra S₂ = S₃ (6)

Từ (4), (6) và kết hợp (1) (2) (3) ta có:

S₁ = S₂ = S₃ = S₄ = S₅ = S₆.