Với giải sách bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 12. Mời các bạn đón xem:

Giải SBT Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 1.11 trang 14 SBT Toán 12 Tập 1: Sử dụng đồ thị dưới đây, xác định xem hàm số y = f(x) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈ hay không.

Lời giải:

Quan sát đồ thị, ta thấy:

Hàm số đạt giá trị lớn nhất tại điểm x₈.

Hàm số đạt giá trị nhỏ nhất tại điểm x₇.

Hàm số đạt cực đại tại điểm x₆.

Hàm số đạt cực tiểu tại điểm x₄ và x₇.

Bài 1.12 trang 14 SBT Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) y = 3x⁴ – 4x³;

b) $y=\frac{x^2}{x-1}$ , x > 1.

Lời giải:

a) y = 3x⁴ – 4x³

Tập xác định: D = ℝ.

Ta có: y' = 12x³ – 12x²

           y' = 0 ⇔ 12x³ – 12x² = 0 ⇔ x = 0 hoặc x = 1.

Từ bảng biến thiên, ta được $\underset{ℝ}{\min }y=y\left(1\right)=-1$ .

Hàn số không có giá trị lớn nhất.

b) $y=\frac{x^2}{x-1}$ , x > 1.

Tập xác định: D = (1; +∞).

Ta có: y' = $\frac{2x\left(x-1\right)-x^2}{{\left(x-1\right)}^2}$  = $\frac{x^2-2x}{{\left(x-1\right)}^2}$

           y' = 0 ⇔ $\frac{x^2-2x}{{\left(x-1\right)}^2}$  = 0 ⇔ x = 2 hoặc x = 0.

Do x > 1 nên x = 0 loại.

Ta có bảng biến thiên như sau:

Từ bảng biến thiên, ta được: $\underset{\left(1;+\infty \right)}{\min }y=y\left(2\right)=4$.

Hàm số không có giá trị lớn nhất trên khoảng (1; +∞).

Bài 1.13 trang 14 SBT Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) y = −x³ + 3x² + 2;

b) $y=\frac{x}{x^2+2}$ .

Lời giải:

a) y = −x³ + 3x² + 2

Tập xác định: D = ℝ.

Ta có: y' = −3x² + 6x

           y' = 0 ⇔ −3x² + 6x = 0 ⇔ x = 0 hoặc x = 2.

Ta có bảng biến thiên như sau:

Từ bảng biến thiên, ta thấy hàm số không có cả giá trị lớn nhất và giá trị nhỏ nhất.

b) $y=\frac{x}{x^2+2}$

Tập xác định: D = ℝ.

Ta có: y' = $\frac{x^2+2-2x^2}{{\left(x^2+2\right)}^2}$  =$\frac{2-x^2}{{\left(x^2+2\right)}^2}$

           y' = 0 ⇔ $\frac{2-x^2}{{\left(x^2+2\right)}^2}$  = 0 ⇔ x = ±$\sqrt{2}$ .

Ta có bảng biến thiên như sau:

Từ bảng biến thiên, ta được:

$\underset{ℝ}{\min }y=y\left(-\sqrt{2}\right)=-\frac{\sqrt{2}}{4}$; $\underset{ℝ}{\max }y=y\left(\sqrt{2}\right)=\frac{\sqrt{2}}{4}$ .

Bài 1.14 trang 14 SBT Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) $f\left(x\right)=x\sqrt{4-x^2}$ , −2 ≤ x ≤ 2;

b) f(x) = x – cosx, $-\frac{\pi }{2}\le x\le \frac{\pi }{2}$.

Lời giải:

a) $f\left(x\right)=x\sqrt{4-x^2}$ , −2 ≤ x ≤ 2

Ta có: f'(x) = $\sqrt{4-x^2}+\frac{-x^2}{\sqrt{4-x^2}}$  = $\frac{4-2x^2}{\sqrt{4-x^2}}$ ;

           f'(x) = 0 ⇔ x = ±$\sqrt{2}$ .

Ta tính được các giá trị: f(−2) = f(2) = 0; f(−$\sqrt{2}$ ) = −2; f( $\sqrt{2}$) = 2.

Do đó, $\underset{\left[-2;2\right]}{\min }f\left(x\right)=f\left(-\sqrt{2}\right)=-2$ ; $\underset{\left[-2;2\right]}{\max }f\left(x\right)=f\left(\sqrt{2}\right)=2$ .

b) f(x) = x – cosx, $-\frac{\pi }{2}\le x\le \frac{\pi }{2}$

Ta có: f'(x) = 1 + sinx

           f'(x) = 0 ⇔ 1 + sinx = 0 ⇔ x = $-\frac{\pi }{2}+k2\pi$  (k ∈ ℤ).

Do $-\frac{\pi }{2}\le x\le \frac{\pi }{2}$ nên x =  (với k = 0).

Ta tính được các giá trị: $f\left(\frac{\pi }{2}\right)=\frac{\pi }{2}$ ; $f\left(-\frac{\pi }{2}\right)=\frac{\pi }{2}$ .

Vậy $\underset{\left[-\frac{\pi }{2};\frac{\pi }{2}\right]}{\min }f\left(x\right)=f\left(-\frac{\pi }{2}\right)=-\frac{\pi }{2}$ , $\underset{\left|-\frac{\pi }{2};\frac{\pi }{2}\right|}{\max }f\left(x\right)=f\left(\frac{\pi }{2}\right)=\frac{\pi }{2}$ .

Bài 1.15 trang 15 SBT Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau:

$f\left(x\right)=\left\{\begin{array}{l}2x-1\text{ nếu 0}\le \text{ x }\le \text{2}\\ x^2-5x+9\text{ nếu 2 < x }\le \text{3.}\end{array}\right.$

Lời giải:

Xét x ∈ (0; 2), ta có: f(x) = 2x – 1

                                  f'(x) = 2 > 0 với mọi x ∈ (0; 2).

Mặt khác, ta có: f(0) = −1, f(2) = 3.

Xét x ∈ (2; 3), ta có: f(x) = x² – 5x + 9

                                f'(x) = 2x – 5

                                f'(x) = 0 ⇔ x = $\frac{5}{2}$  (thỏa mãn).

Mặt khác, f $\left(\frac{5}{2}\right)$ =$\frac{11}{4}$ ; f(3) = 3.

Vậy $\underset{\left[0;3\right]}{\min }f\left(x\right)$  = f(0) = −1; $\underset{\left[0;3\right]}{\max }f\left(x\right)$  = f(2) = f(3) = 3.       

Bài 1.16 trang 15 SBT Toán 12 Tập 1: Lợi nhuận thu được P của một công ty khi dùng số tiền s chi cho quảng cáo được cho bởi công thức

P = P(s) = $-\frac{1}{10}$s³ + 6s² + 400, s ≥ 0.

Ở đây các số được tính bằng đơn vị nghìn USD.

a) Tìm số tiền công ty phải chi cho quảng cáo để mang lại lợi nhuận tối đa.

b) Lợi nhuận thu được của công ty thay đổi thế nào khi số tiền chi cho quảng cáo thay đổi?

Lời giải:

a) Ta có: P' = $-\frac{3}{10}$ s² + 12s

               P' = 0 ⇔ $-\frac{3}{10}$ s² + 12s = 0 ⇔ s = 0 hoặc s = 40.

Ta có bảng biến thiên:

Vậy để mang lại lợi nhuận tối đa, số tiền công ty phải chi cho quảng cáo là 40 nghìn USD.

b) Từ bảng biến thiên, suy ra:

Lợi nhuận của công ty tăng dần khi số tiền chi cho quảng cáo tăng từ 0 đến 40 nghìn USD

Lợi nhuận của công ty giảm dần khi số tiền chi cho quảng cáo lớn hơn 40 nghìn USD và khi đó, càng tăng tiền quảng cáo thì lợi nhuận càng giảm.

Bài 1.17 trang 15 SBT Toán 12 Tập 1: Giả sử một chiếc xe tải khi di chuyển với tốc độ x dặm/giờ sẽ tiêu thụ nhiên liệu ở mức $\frac{1}{200}\left(\frac{2500}{x}+x\right)$  gallon/dặm. Nếu giá nhiên liệu là 3,6 USD/gallon thì chi phí nhiên liệu C (tính bằng USD) khi lái xe 200 dặm với tốc dộ x dặm/giờ được cho bởi công thức

C = C(x) = $3,6.\left(\frac{2500}{x}+x\right)$ .

Ở đây, dặm và gallon là những đơn vị đo lường phổ biến của Mỹ. Biết rằng tốc độ (dặm/giờ) của xe tải trên một tuyến đường cao tốc bị hạn chế trong khoảng [10; 75]. Hỏi:

a) Lái xe ở tốc độ nào thì chi phí nhiên liệu sẽ ít nhất?

b) Nếu người lái xe tải được trả lương 28 USD/ giờ và tiền lương được cộng vào chi phí nhiên liệu thì tốc độ di chuyển của xe tải là bao nhiêu để chi phí tiết kiệm nhất (tức là tổng chi phí mà công ty phải trả cho lái xe và chi phí nhiên liệu là nhỏ nhất)?

Lời giải:

a) Ta có: C = C(x) = $3,6.\left(\frac{2500}{x}+x\right)$  với x ∈ [10; 75].

                      C'(x) = 3,6.$\left(-\frac{2500}{x^2}+1\right)$

                      C'(x) = 0 ⇔ x = 50 (do x ∈[10; 75]).

Xét trên đoạn [10; 75], ta tính được: C(10) = 936; C(50) = 360; C(75) = 390.

Vậy xe tải đi với tốc độ 50 dặm/giờ thì chi phí nhiên liệu sẽ ít nhất.

b) Trong trường hợp người lái xe tải được trả lương 28 USD/giờ (khi xe chạy) thì chi phí C(X) khi lái xe s dặm là:

C(x) = 28.$\frac{s}{x}$  + $\frac{s}{200}\left(\frac{2500}{x}+x\right)$  = $s.\left(\frac{81}{2x}+\frac{x}{200}\right)$ .

Ta có: C'(x) = $s\left(-\frac{81}{2x^2}+\frac{1}{100}\right)$.

Suy ra C'(x) < 0 với mọi x ∈ [10; 75], tức là hàm số C(x) nghịch biến trên đoạn [10; 75]

Vậy xe phải di chuyển với tốc độ 72 dặm/ giờ thì tiết kiệm chi phí nhất.

Bài 1.18 trang 15 SBT Toán 12 Tập 1: Hai nguồn nhiệt đặt cách nhau s mét, một nguồn có cường độ a đặt ở điểm A và một nguồn có cường độ b đặt ở điểm B. Cường độ nhiệt tại điểm P nằm trên đoạn thẳng nối A và B được tính theo công thức

 $I=\frac{a}{x^2}+\frac{b}{{\left(s-x\right)}^2}$

trong đó x (m) là khoảng cách giữa P và A. Tại điểm nào nằm giữa A và B nhiệt độ sẽ thấp nhất?

Lời giải:

Xét hàm số: $I=\frac{a}{x^2}+\frac{b}{{\left(s-x\right)}^2}$ , 0 < x < s.

Ta có: I' = $-\frac{2\mathrm{a}}{{\mathrm{x}}^3}+\frac{2\mathrm{b}}{\left(\mathrm{s}-\mathrm{z}\right)}=\frac{2\left[{\mathrm{bx}}^3-\mathrm{a}{\left(\mathrm{s}-\mathrm{x}\right)}^3\right]}{{\mathrm{x}}^3{\left(\mathrm{s}-\mathrm{x}\right)}^3}$ , 0 < x < s.

Do đó: I' = 0 ⇔ $\frac{x}{s-x}=\frac{\sqrt[3]{a}}{\sqrt[3]{b}}$  ⇔ x = $\frac{s\sqrt[3]{a}}{\sqrt[3]{a}+\sqrt[3]{b}}$ .

Ta có bảng biến thiên như sau:

Vậy tại điểm P trên AB và cách A một khoảng PA = x = $\frac{s\sqrt[3]{a}}{\sqrt[3]{a}+\sqrt[3]{b}}$  (m) thì nhiệt độ thấp nhất.

Bài 1.19 trang 16 SBT Toán 12 Tập 1: Một vật được phóng lên trời theo một góc xiên θ (45° ≤ x ≤ 90°) so với phương ngang với vận tốc ban đầu v₀ (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc 45° so với phương ngang (xem hình vẽ). Nếu bỏ qua sức cản của không khí thì quãng đường R (tính bằng feet, 1 feet = 0,3048 m) mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số

R(θ) = $\frac{v_0^2\sqrt{2}}{16}\cos \theta \left(\sin \theta -\cos \theta \right).$          

Góc nén θ nào làm cho quãng đường R lớn nhất? Giá trị lớn nhất của R là bao nhiêu?

Lời giải:

Ta có: R(θ) = $\frac{v_0^2\sqrt{2}}{16}\left(\cos \theta \sin \theta -{\cos }^2\theta \right)$  = $\frac{v_0^2\sqrt{2}}{32}\left(\sin 2\theta -\cos 2\theta -1\right)$ , 45° ≤ θ ≤ 90°.

Do đó: R'(θ) = $\frac{v_0^2\sqrt{2}}{16}\left(\cos 2\theta +\sin 2\theta \right)$

            R'(θ) = 0 ⇔ 2θ = 135° ⇔ θ = 67,5° (do 45° ≤ θ ≤ 90°).

Mặt khác, R(45°) = 0; R(67,5°) = $\frac{v^2\left(2-\sqrt{2}\right)}{32}$ ; R(90°) = 0.

Ta có bảng biến thiên như sau:

Vậy khi góc ném θ = 67,5° thì quãng đường R là lớn nhất và bằng $\frac{v^2\left(2-\sqrt{2}\right)}{32}$ feet, trong đó v₀ (feet/giây) là vận tốc ban đầu của vật.

Bài 1.20 trang 16 SBT Toán 12 Tập 1: Một chiếc xe nhỏ chuyển động không có ma sát, gắn vào tường bằng một lò xo (xem hình vẽ), được kéo ra khỏi vị trí đứng yên 10 cm rồi thả ra tại thời điểm ban đầu t = 0 giây để chuyển động trong 4 giây. Vị trí s (cm) tại thời điểm t giây là s = 10cosπt.

a) Tốc độ lớn nhất của xe là bao nhiêu? Khi nào xe chuyển động với tốc độ như vậy, khi đó xe đang ở vị trí nào và gia tốc lúc đó có độ lớn là bao nhiêu?

b) Xe ở đâu khi độ lớn gia tốc là lớn nhất? Khi đó vận tốc của xe là bao nhiêu?

Lời giải:

a) Vận tốc của xe là v(t) = s'(t) = −10πsinπt (cm/s).

Do đó, gia tốc của xe là a(t) = v'(t) = −10π²cosπt (cm/s²).

Ta có: v'(t) = 0 ⇔ t ∈ $\left\{\frac{1}{2};\frac{3}{2};\frac{5}{2};\frac{7}{2}\right\}$  (do t ∈ [0; 4]).

Mặt khác, v(0) = v(4) = 0; v$\left(\frac{1}{2}\right)$  = v$\left(\frac{3}{2}\right)$  = v$\left(\frac{5}{2}\right)$  = v$\left(\frac{7}{2}\right)$  = −10π.

Tốc độ của độ lớn của vận tốc, tức là $\left|v\left(t\right)\right|$ .

Vậy tốc độ lớn nhất của xe là 10π (cm/s), đạt được tại các thời điểm: $\frac{1}{2};\frac{3}{2};\frac{5}{2};\frac{7}{2}$  giây.

Tại các thời điểm đó, xe đều có gia tốc bằng 0 và tại các vị trí s = 0 (tức là ở vị trí xe đứng yên, khi mà chưa kéo lò xo).

b) Ta có: a'(t) = 10π³sinπt

               a'(t) = 0 ⇔ t ∈ {0; 1; 2; 3; 4}.

Khi đó, a(0) = a(2) = a(4) = −10π²; a(1) = a(3) = 10π².

Độ lớn gia tốc của xe là $\left|a\left(t\right)\right|$ .

Do đó, độ lớn gia tốc là lớn nhất tại các thời điểm 0; 1; 2; 3; 4 giây.

Khi t = 0; 2; 4 giây, xe ở vị trí s = 10 (cm); khi t = 1; 3 giây, xe ở vị trí s = −10 (cm).

Vậy độ lớn của gia tốc của xe lớn nhất tại các vị trí s = 10 (cm) hoặc s = −10 (cm) (tức là khi xe ở mép phải hoặc mép trái của quãng đường dao động) và tại các vị trí đó, vận tốc của xe đều bằng 0.

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

1. Định nghĩa

Khái niệm GTLN, GTNN của hàm số

Cho hàm số y = f(x) xác định trên tập D. - Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) $\le$ M với mọi $x\in D$ và tồn tại $x_0\in D$ sao cho $f(x_0)$ = M. Kí hiệu M = $\underset{x\in D}{max}f(x)$ hoặc M = $\underset{D}{max}f(x)$ - Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) $\ge$ m với mọi $x\in D$ và tồn tại $x_0\in D$ sao cho $f(x_0)$ = m. Kí hiệu m = $\underset{x\in D}{min}f(x)$ hoặc m = $\underset{D}{min}f(x)$

Ví dụ: Tìm GTLN, GTNN của hàm số $y=f(x)=\sqrt{1-x^2}$

Tập xác định của hàm số là $\left[-1;1\right]$

Ta có:

$f(x)=\sqrt{1-x^2}$ $\ge$ 0; dấu bằng xảy ra khi $1-x^2=0$, tức x = -1 hoặc x = 1.

Do đó $\underset{x\in \left[-1;1\right]}{min}f(x)=f(-1)=f(1)=0$

$f(x)=\sqrt{1-x^2}$ $\le 1$; dấu bằng xảy ra khi $1-x^2=1$, tức x = 0.

Do đó $\underset{x\in \left[-1;1\right]}{max}f(x)=f(0)=1$

2. Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Giả sử y = f(x) là hàm số liên tục trên $\left[a;b\right]$ và có đạo hàm trên (a;b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn $\left[a;b\right]$ mà đạo hàm f’(x) = 0. Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn $\left[a;b\right]$: Tìm các điểm $x_1,x_2,...,x_n\in (a;b)$, tại đó f’(x) = 0 hoặc không tồn tại Tính $f(x_1),f(x_2),...,f(x_n),f(a)$ và $f(b)$ Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có: M = $\underset{\left[a;b\right]}{max}f(x)$; m = $\underset{\left[a;b\right]}{min}f(x)$

Ví dụ: Tìm GTLN và GTNN của hàm số $y=x^4-4x^2+3$ trên đoạn $\left[0;4\right]$

Ta có: $y^{\prime }=4x^3-8x=4x(x^2-2);y^{\prime }=0\iff x=0$ hoặc $x=\sqrt{2}$ (vì $x\in \left[0;4\right]$)

            y(0) = 3; y(4) = 195; y($\sqrt{2}$) = -1

Do đó: $\underset{\left[0;4\right]}{max}y=y(4)=195$; $\underset{\left[0;4\right]}{min}y=y(\sqrt{2})=-1$

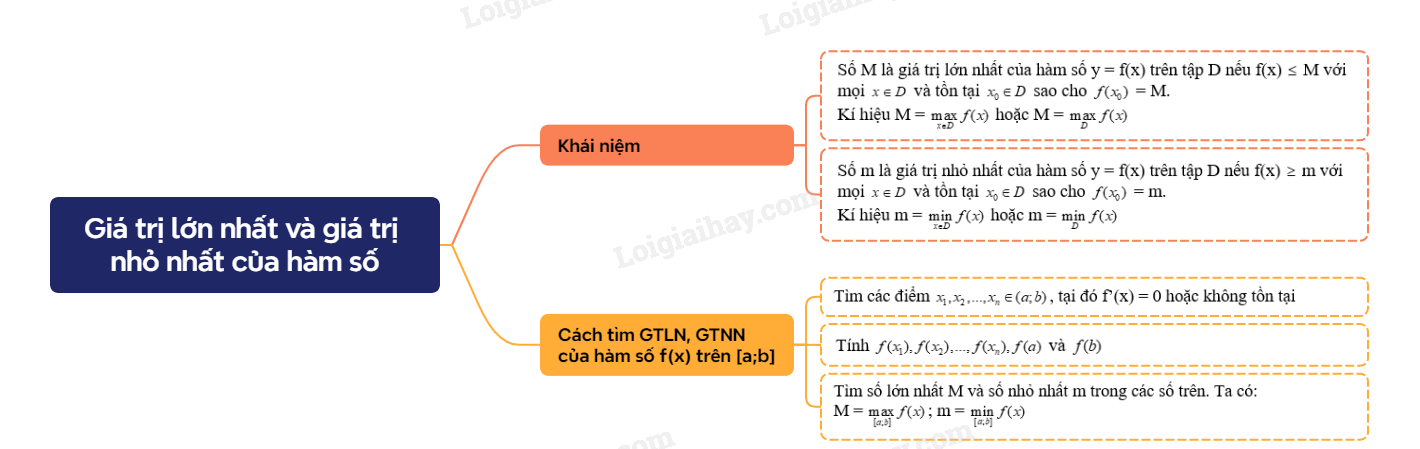
Sơ đồ tư duy Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Xem thêm các bài giải SBT Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài 1: Tính đơn điệu và cực trị của hàm số

Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 3: Đường tiệm cận của đồ thị hàm số

Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

Bài tập cuối chương 1