Tailieumoi.vn xin giới thiệu Tìm m để phương trình có nghiệm 2024 đầy đủ, chi tiết được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Tìm m để phương trình có nghiệm. Mời các bạn đón xem:

Tìm m để phương trình có nghiệm 

A. Lý thuyết Tìm m để phương trình có nghiệm

Cho phương trình: ax² + bx + c = 0 (a ≠ 0)

1. Điều kiện để phương trình có hai nghiệm phân biệt sao cho x₁ = px₂ (với p là một số thực)

B1- Tìm điều kiện để phương trình có hai nghiệm phân biệt .

B2- Áp dụng định lý Vi - ét tìm:

B3- Kết hợp (1) và (3) giải hệ phương trình: 

B4- Thay x₁ và x₂ vào (2) ⇒ Tìm giá trị tham số.

2. Điều kiện để phương trình có hai nghiệm thỏa mãn điều kiện: |x₁ - x₂| = k(k ∈ R)

- Bình phương trình hai vế: (x₁ - x₂)² = k² ⇔ ... ⇔ (x₁ + x₂)² - 4x₁x₂ = k²

- Áp dụng định lý Vi-ét tính x₁ + x₂ và x₁x₂ thay vào biểu thức ⇒ kết luận.

3. So sánh nghiệm của phương trình bậc hai với một số bất kỳ:

B1: Tìm điều kiện để phương trình có nghiệm (∆ ≥ 0)

B2: Áp dụng Vi-ét tính x₁ + x₂ và x₁x₂  (*)

+/ Với bài toán: Tìm m để phương trình có hai nghiệm > α

Ta có: 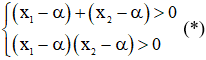. Thay biểu thức Vi-ét vào hệ(*) để tìm m

+/ Với bài toán: Tìm m để phương trình có hai nghiệm < α

Ta có: 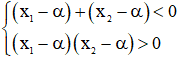  (*).Thay biểu thức Vi-ét vào hệ(*) để tìm m

+/ Với bài toán: Tìm m để phương trình có hai nghiệm: x₁ < α < x₂

Ta có: (x₁ - α)(x₂ - α) < 0 (*). Thay biểu thức Vi-ét vào (*) để tìm m

B. Bài tập Tìm m để phương trình có nghiệm

1. Bài tập tự luận

Câu 1: Cho phương trình x² - (2m + 2)x + 2m = 0 (m là tham số). Tìm m để phương trình có hai nghiệm x₁, x₂ thỏa mãn 

A. m = 0

B. m = 1

C. m = 3

D. m = 4

Lời giải:

Phương trình x² - (2m + 2)x + 2m = 0 ⇔ x² - 2(m + 1)x + 2m = 0

Điều kiện PT có 2 nghiệm không âm x₁, x₂ là

Vậy m = 0 là giá trị cần tìm.

Đáp án đúng là A

Câu 2: Cho phương trình x² + 2x - m² - 1 = 0 (m là tham số)

Tìm m để phương trình trên có hai nghiệm thỏa mãn x₁ = -3x₂

A. m = 3

B. m = ±1

C. m = ±√2

D. m = -2

Lời giải:

Ta có: Δ' = 1² - 1.(-m² - 1)=1 + m² + 1 = m² + 2 > 0 (luôn đúng với mọi m)

Suy ra phương trình luôn có hai nghiệm phân biệt với mọi m.

Theo Vi-ét ta có: 

Ta có: x₁ + x₂ = -2 (do trên) và x₁ = -3x₂ nên có hệ phương trình sau:

Thay (*) vào biểu thức x₁.x₂ = -m² - 1 ta được:

Vậy m = ±√2 là các giá trị cần tìm.

Đáp án đúng là C

Câu 3: Cho phương trình x² - 2(m + 1)x + m² + m - 1 = 0 (m là tham số)

Gọi S là tập tất cả các giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện 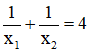. Tính tích của các giá trị đó

Lời giải:

Δ' = (m + 1)² - (m² + m - 1) = m² + 2m + 1 - m² - m + 1 = m + 2

Phương trình đã cho có hai nghiệm phân biệt ⇔ Δ' > 0 ⇔ m + 2 > 0 ⇔ m > -2

Áp dụng hệ thức Vi-ét, ta có: 

Do đó:

Kết hợp với điều kiện m > -2 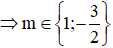 là các giá trị cần tìm.

Đáp án đúng là C

Câu 4: Cho phương trình 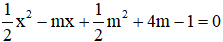 (m là tham số).  Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm thỏa mãn 

Lời giải:

Để phương trình đã cho có hai nghiệm phân biệt thì ∆ ≥ 0

Phương trình có nghiệm khác 0 

Kết hợp với điều kiện 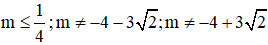 ta có

Vậy 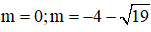 là các giá trị cần tìm.

Đáp án đúng là B

Câu 5: Cho phương trình 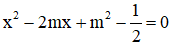  (m là tham số).

Tìm m để phương trình có hai nghiệm là số đo của 2 cạnh góc vuông của tam giác vuông có cạnh huyền bằng 3.

A. m = ±2

B. m = ±√2

C. m = - 1

D. m = 0

Lời giải:

Ta có: 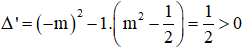, luôn đúng với mọi m

Suy ra phương trình luôn có hai nghiệm phân biệt với mọi giá trị m.

Giả sử phương trình có hai nghiệm là x₁, x₂.

Áp dụng Vi-et ta có: 

Theo đề bài x₁, x₂ là số đo của 2 cạnh góc vuông của tam giác vuông có cạnh huyền bằng 3 nên ta có:

Vậy m = ±2  là các giá trị cần tìm.

Đáp án đúng là A

Câu 6: Cho phương trình x² - 2x - 2m² = 0 với x là ẩn số.

Tìm giá trị của m để hai nghiệm của phương trình thỏa hệ thức x₁² = 4x₂².

A. m = ±2

B. m = ±1

C. m = -6

D. m = 3

Lời giải:

Ta có: Δ' = (-1)² - (-2m² )= 1 + 2m² > 0

Suy ra phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.

Giả sử phương trình có hai nghiệm x₁, x₂ theo hệ thức Vi-ét:

Vậy m = ±2 là giá trị cần tìm.

Đáp án đúng là A

Câu 7: Cho phương trình x² – 5x + m = 0 (m là tham số).

Tìm m để phương trình trên có hai nghiệm x₁, x₂ thỏa mãn |x₁ - x₂| = 3.

A. m = 2

B. m = 4

C. m = 6

D. m = 8

Lời giải:

Ta có: ∆ = 25 – 4m

Để phương trình đã cho có 2 nghiệm phân biệt x₁, x₂ thì 

Theo Vi-ét, ta có: x₁ + x₂  = 5 (1) và x₁.x₂ = m (3)

Mặt khác theo giả thiết ta có: |x₁ - x₂| = 3 (2)

Giải hệ (1) và (2):

Với x₁ = 4, x₂ = 1 thay vào (3) ta được m = 4

Với x₁ = 1, x₂ = 4 thay vào (3) ta được m = 4

m = 4 thỏa mãn điều kiện (*) , vậy m = 4 là giá trị cần tìm

Đáp án đúng là B

Câu 8: Cho phương trình bậc hai x² + 2(m - 1)x - (m + 1)= 0

Tìm giá trị m để phương trình có một nghiệm lớn hơn  và một nghiệm nhỏ hơn 1.

Lời giải:

Ta có: 

Suy ra phương trình luôn có hai  nghiệm phân biệt x₁, x₂ với mọi m.

Theo hệ thức Vi- ét ta có: 

Để phương trình có một nghiệm lớn hơn , một nghiệm nhỏ hơn 1 thì (x₁ - 1)(x₂ - 1) < 0

Đáp án đúng là C

Câu 9: Cho phương trình bậc hai: x² + 2(m - 1)x - (m + 1) = 0

Tìm giá trị m để phương trình có hai nghiệm lớn hơn 2

A. m > - 1

B. m > 2

C. m < 2

D. m < 0

Lời giải:

Ta có: 

Suy ra phương trình luôn có hai  nghiệm phân biệt x₁, x₂ với mọi m.

Theo hệ thức Vi- ét ta có: 

Để phương trình có hai nghiệm đều nhỏ hơn 2 thì:

Vậy đáp án đúng là D

Câu 10: Cho phương trình x² - (2m + 3)x + m² + 3m + 2 = 0

Xác định m để phương trình có hai nghiệm thỏa mãn -3 < x₁ < x₂ < 6

A. m > 1

B. -2 < m < 2

C. -4 < m < 4

D. m < 3

Lời giải:

Phương trình đã cho luôn có hai nghiệm phân biệt với mọi m.

Theo hệ thức Vi-et ta có: 

Vì -3 < x₁ < x₂ < 6 nên

Vậy -4 < m < 4.

Đáp án đúng là C

2. Bài tập tự luyện

Bài 1. Tìm các giá trị của tham số m để các phương trình sau có hai nghiệm phân biệt:

a) x² + 2x + m = 0;

b) – x² + 2mx – m² – m = 0;

c) mx² – 3(m + 1)x + m² – 13m – 6 = 0.

Bài 2. Cho phương trình x² – (– 4m – 1)x + 2(m – 4) = 0. Tìm các giá trị của m để phương trình có hai nghiệm x₁, x₂ thỏa mãn:

a) x₂ – x₁ = 17;

b) Biểu thức A = (x₁ – x₂)² có giá trị nhỏ nhất;

c) Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào m.

Bài 3. Cho phương trình x² – 5x + m + 4 = 0 (m là tham số). Gọi x₁, x₂ là hai nghiệm của phương trình. Tìm giá trị của m để phương trình thỏa mãn:

 x₁(1 – 3x₂) + x₂(1 – 3x₁) = m² – 23.

Bài 4. Cho phương trình x² – (2m + 1)x + m² + m – 6 = 0.

a) Chứng minh phương trình luôn có hai nghiệm phân biệt;

b) Tìm các giá trị của m để phương trình có hai nghiệm phân biệt;

c) Gọi x₁, x₂ là hai nghiệm của phương trình. Tìm giá trị nhỏ nhất của biểu thức $A=x_1^2+x_2^2;$;

d) Tìm các giá trị của m để phương trình có hai nghiệm x₁, x₂ thỏa mãn $\left|x_1^3+x_2^3\right|=19$

Bài 5. Cho hai phương trình x² – mx – m – 1 = 0. Tìm các giá trị của tham số m để phương trình

a) Có hai nghiệm x₁, x₂ thỏa mãn $x_1^3+x_2^3=-1$;

b) Có hai nghiệm x₁, x₂ thỏa mãn $\left|x_1-x_2\right|\ge 3$;

c) Có hai nghiệm x₁, x₂. Từ đó, hãy lập phương trình bậc hai có u và v là nghiệm biết rằng $u=x_1+\frac{1}{x_2}$ và $v=x_2+\frac{1}{x_1}$.