Tailieumoi.vn xin giới thiệu Bài tập Bài toán chuyển động - Giải bài toán bằng cách lập hệ phương trình có đáp án được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán . Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Bài toán chuyển động - Giải bài toán bằng cách lập hệ phương trình có đáp án. Mời các bạn đón xem:

Bài tập Bài toán chuyển động - Giải bài toán bằng cách lập hệ phương trình có đáp án

A. Bài tập Bài toán chuyển động - Giải bài toán bằng cách lập hệ phương trình có đáp án

1. Bài tập trắc nghiệm

Câu 1: Một ô tô đi quãng đường AB với vận tốc 50km/h rồi đi tiếp quãng đường BC với vận tốc 45km/h. Biết quãng đường tổng cộng dài 165km và thời gian xe đi trên quãng đường AB ít hơn thời gian trên quãng đường BC là 30 phút. Tính thời gian ô tô đi trên quãng đường AB.

A. 1 giờ

B. 1,5 giờ

C. 2 giờ

D. 2,5 giờ

Lời giải:

Đáp án: B

Gọi thời ô tô đi trên quãng đường AB và BC lần lượt là x (giờ), y (giờ) (x,y > 0)

Đổi 30 phút = 0,5h

Vì tổng độ dài quãng đường là 165km, nên ta có phương trình: 50x + 45y = 165

Vì thời gian xe đi trên quãng đường AB ít hơn thời gian trên quãng đường BC là 30 phút, ta có: x + 0,5 = y

thay y = x + 0,5 vào pt (1) ta được:

50x + 45(x + 0,5) = 165 ⇔ 95x + 22,5 = 165

⇔ 95x = 142,5 ⇔ x = 1,5 ( tm )

Với x = 1,5 → y = 2 (tm )

Vậy vận tốc của ô tô trên AB là: 1,5 giờ. Chọn đáp án B.

Câu 2: Một người đi xe đạp từ địa điểm A đến B trong một thời gian đã định với vận tốc không đổi. Nếu người đó tăng vận tốc lên 3km/h thì đến B sớm hơn dự định 1 giờ. Nếu người đó giảm vận tốc 2km/h thì đến B muộn hơn dự định 1 giờ. Tính quãng đường AB.

A. 40km    B. 50km     C. 60km     D. 70km

Lời giải:

Đáp án: C

Gọi vận tốc dự định là x (km/h), thời gian dự định là y (giờ) (x > 0, y > 0)

Độ dài quãng đường AB là : xy ( km)

Vì người đó tăng vận tốc lên 3 km/h thì sẽ đến B sớm hơn dự định 1 giờ, tức là nếu đi với vận tốc x + 3 km/h thì thời gian là y -1 giờ. Khi đó độ dài quãng đường là (x + 3)(y – 1).

Vì người đó giảm vận tốc 2 km/h thì sẽ đến B muộn hơn dự định 1 giờ, tức là nếu đi với vận tốc x-2 km/h thì thời gian là y + 1 giờ. Khi đó độ dài quãng đường là (x – 2)(y + 1).

Cộng vế theo vế của hai phương trình ta được: y = 5 (tm)

Với y = 5 → x = (2 + 2.5) = 12.( tm )

Vậy quãng đường AB là 5 x 12 = 60km.

Câu 3: Một ca nô chạy trên sông trong 5h, xuôi dòng 78km và ngược dòng 44km. Với vận tốc dự định nếu ca nô xuôi dòng 13km và ngược dòng 11km với vận tốc dự định đó thì mất 1 giờ. Hãy tính vận tốc riêng của ca nô,biết vận tốc dòng nước và vận tốc riêng của ca nô là không đổi.

A. 24km/h

B. 36km/h

C. 72km/h

D.54km/h

Lời giải:

Đáp án: A

Gọi vận tốc ca no khi nước yên lặng là x km/h.(x>y)

Gọi vận tốc của dòng nước là y km/h (y > 0)

Vận tốc ca no đi xuôi dòng là: x+y (km/h)

Vận tốc ca no đi ngược dòng là: x-y (km/h)

Vì ca nô chạy trên sông trong 5h, xuôi dòng 78km và ngược dòng 44km, ta có phương trình:

Vì ca nô chạy trên sông trong 1h, xuôi dòng 13km và ngược dòng 11km, ta có phương trình:

Cộng vế theo vế của hai phương trình trên ta được: 2x = 48 ⇔ x = 24 ( tm )

Với x = 24 → y = 2 ( tm )

Vậy vận tốc riêng của ca nô là 24km/h.

Câu 4: Một chiếc thuyền xuôi dòng, ngược dòng trên khúc sông dài 40km hết 4 giờ 30 phút. Biết thời gian xuôi dòng 5km bằng thời gian ngược dòng 4km. Tính vận tốc dòng nước?

A. 1     B. 2     C. 3     D. 4

Lời giải:

Đáp án: B

Gọi vận tốc của thuyền khi dòng nước yên lặng là: x (km/h), (x > y)

Vận tốc của dòng nước là y (km/h), (y > 0)

Vận tốc của thuyền khi xuôi dòng là: x + y ( km/h)

Vận tốc của thuyền khi ngược dòng là: x - y ( km/h)

Vì thời gian xuôi dòng 5km bằng thời gian ngược dòng 4km, nên ta có phương trình:

Vì thuyền xuôi dòng, ngược dòng trên khúc sông dài 40km hết 4 giờ 30 phút = 9/2 giờ, ta có:

Cộng vế theo vế của hai phương trình trên ta được: 2x = 36 ⇔ x = 18 ( tm )

Với x = 18 → y = 2 ( tm )

Vậy vận tốc của dòng nước là 2 km/h.

Câu 5: Một ô tô đi từ A đến B với tốc xác định, trong thời gian đã định. Nếu vận tốc giảm 10km/h thì thời gian tăng lên 45 phút, nếu vận tốc tăng 10km/h thì thời gian giảm 30 phút. Thời gian dự định của ô tô?

A. 1     B.2     C. 3     D.4

Lời giải:

Đáp án: C

Gọi vận tốc dự đinh của ô tô là x (km/h), ( x > 10)

Thời gian dự định của ô tô là y (km/h) ( y > 0,5)

Vì vận tốc giảm 10km/h thì thời gian tăng lên 45 phút, nên ta có:

Vì vận tốc tăng 10km/h thì thời gian giảm 30 phút, nên ta có:

Nhân pt (2) với 3 ta được: –3x + 60y = 30, rồi cộng với pt (1) ta được:

20y = 60 ⇔ y = 3 ( tm)

Với y = 2 → x = 50 ( tm)

Vậy thời gian dự đinh của ô tô là: 3 giờ.

Câu 6: Hai ô tô cùng khởi hành một lúc từ 2 tỉnh A và B cách nhau 400km đi ngược chiều và gặp nhau sau 5giờ. Nếu vận tốc của mỗi xe không thay đổi nhưng xe đi chậm xuất phát trước xe kia 40 phút thì 2 xe gặp nhau sau 5 giờ 22 phút kể từ lúc xe chậm khởi hành. Tính vận tốc xe chạy chậm.

A. 44     B. 54     C. 60     D. 36

Lời giải:

Đáp án: D

Gọi vận tốc của xe nhanh là x (km/h), vận tốc của xe chậm là là y (km/h)(x,y>0)

Hai xe cùng khởi hành một lúc và đi ngược chiều sau 5h gặp nhau, nên ta có phương trình: 5(x+y) = 400

Thay x = 80 – y vào pt (2) ta được:

141(80 – y) + 161y = 12000

⇔ 11280 – 141y + 161y = 12000 ⇔ 20y = 720 ⇔ y = 36

Với y = 36 → x = 80 – 36 = 44 (tm).

Vậy vận tốc xe chạy chậm là 36 km/h.

Câu 7: Một ô tô và xe đạp chuyển động từ hai đầu một quãng đường, Sau 3 giờ thì hai xe gặp nhau, nếu chuyển động cùng chiều và xuất phát tại cùng một địa điểm thì sau 1 giờ hai xe cách nhau 28km. Tính vận tốc xe đạp biết quãng đường dài 156 km.

A. 12     B. 24     C. 36     D. 42

Lời giải:

Đáp án: A

Gọi vận tốc của xe đạp và ô tô lần lượt là x (km/h) và y (km/h), ( x, y > 0)

Vì sau 3 giờ thì hai xe gặp nhau, nên ta có phương trình: 3x + 3y = 156

Vì sau 1 giờ hai xe cách nhau 28km, khi xuất phát tại một điểm, ta có phương trình: y – x = 28

Suy ra hệ phương trình:

Nhân pt (2) với 3 ta được: –3x + 3y = 84, rồi cộng với pt(1) ta được:

6y = 240 ⇔ y = 40 (tm )

Với y = 40 → x = 12 (tm )

Vậy vận tốc của xe đạp là 12 km/h

Câu 8: Một ô tô dự định đi từ A đến B với thời gian nhất định. Nếu chạy với vận tốc 35km/h thì đến B chậm hơn 2 giờ so với dự định. Nếu chạy với vận tốc 50km/h thì đến B sớm hơn 1 giờ so với dự định. Tính quãng đường AB?

A. 250     B. 350     C. 420     D. 360

Lời giải:

Đáp án: B

Gọi quãng đường AB là x (km), thời gian dự định ô tô đi từ A đến B là y (giờ), ( x > 0, y > 1)

Vì nếu chạy với vận tốc 35km/h thì đến B chậm hơn 2 giờ so với dự định, ta có phương trình:

Vì nếu chạy với vận tốc 50km/h thì đến B sớm hơn 1 giờ so với dự định, ta có:

Suy ra hệ phương trình:

Cộng pt(1) và pt (2) ta được:

Với x = 350 => y = 8 (tm )

Vậy quãng đường AB dài 350km

Câu 9: Hai ca nô đi ngược chiều nhau và khởi hành cùng lúc trên dòng sông dài 85km. Sau 1 giờ 40 phút thì gặp nhau. Tính vận tốc thật của mỗi ca nô, biết rằng vận tốc ca nô xuôi dòng lớn hơn vận tốc ca nô ngược dòng là 9km/h, và vận tốc dòng nước là 3km/h.

A. 27km/h và 24km/h

B. 30km/h và 36km/h

C. 36km/h và 40km/h

D. 42km/h và 48km/h

Lời giải:

Đáp án: A

Gọi vận tốc thật của ca nô xuôi dòng là x (km/h), (x > 3)

Vận tốc ca nô ngược dòng là y (km/h),(y > 3)

Vì hai ca nô đi ngươc chiều nhau và khời hành cùng lúc trên dòng sông dài 85km, ta có:

Vì vận tốc ca nô xuôi dòng lớn hơn vận tốc ca nô ngược dòng là 9km/h, ta có:

(x+3)-(y-3)=9 ⇔ x-y=3

Suy ra hệ phương trình:

Cộng hai phương trên với nhau ta được: 2x = 54 ⇔ x = 27 (tm)

Với x = 27 → y = 24 ( tm)

Vậy vận tốc thực của ca nô xuôi dòng là 27km/h và vận tốc ca nô ngược dòng là 24km/h.

Câu 10: Hai tỉnh A và B cách nhau 180km, cùng một lúc ô tô đi từ A đến B và xe máy đi từ B về A. Hai xe gặp nhau tại thị trấn C, từ C đến B ô tô đi hết 2 giờ còn từ C về A xe máy đi hết 4 giờ 30 phút. Tính vận tốc của ô tô, biết rằng hai xe chạy trên AB không đổi.

A. 24km/h

B. 48km/h

C. 36km/h

D. 54km/h

Lời giải:

Đáp án: C

Đổi 4 giờ 30 phút = 4,5 giờ

Gọi vận tốc của ô tô là x (km/h), vận tốc của xe máy là y (km/h), (x, y > 0)

Vì hai xe gặp nhau tại thị trấn C, từ C đến B ô tô đi hết 2 giờ còn từ C về A xe máy đi hết 4 giờ 30 phút = 4,5 h , ta có phương trình: 2x + 4,5y = 180.

Vì hai xe đi cùng một lúc và gặp nhau tại thị trấn C nên thời gian hai xe đến C là như nhau, ta có:

Thay x = 1,5 y vào pt (1) ta có:

2.(1,5 y) + 4,5y = 180 ⇔ 3y + 4,5y = 180 ⇔ 7,5 y = 180 ⇔ y = 24 ( tm )

Với y = 24 → x = 36 ( tm)

Vậy vận tốc của ô tô là 36 km/h.

Câu 11: Hai ô tô cùng khởi hành một lúc từ 2 tỉnh A và B cách nhau 400km đi ngược chiều và gặp nhau sau 5h. Nếu vận tốc của mỗi xe không thay đổi nhưng xe đi chậm xuất phát trước xe kia 40 phút thì 2 xe gặp nhau sau 5h22 phút kể từ lúc xe chậm khởi hành. Tính vận tốc mỗi xe

Lời giải:

Gọi vận tốc của xe nhanh là x km/h, vận tốc của xe chậm là y km/h (x, y > 0).

Hai xe cùng khởi hành một lúc và đi ngược chiều sau 5h gặp nhau nên ta có phương trình 5(x+y)=400 (1)

Thời gian xe đi chậm hết 

Thời gian xe đi nhanh hết  giờ

Vì xe đi chậm xuất phát trước 

Quãng đường xe đi chậm đi được là 

Quãng đường xe đi nhanh đi được là 

Cả 2 xe đi được 

Từ (2) 

Từ (1) 

X = 80 - y thay vào (3)

141(80y - y) + 161y = 1200

11280 - 141y + 161y = 12000

20y = 12000 - 11280

20y = 720

y = 720 / 20 = 36km/h

Thay y =  36 vào

X - 80 - 36 = 44km/h

Vậy vận tốc của xe nhanh là 44km/h

       vận tốc của xe chậm là 36km/h

2. Bài tập tự luyện

Bài 1: Một tàu thủy xuôi dòng trên một khúc sông từ bến A đến bến B dài 160km. Sau đó ngược dòng trên khúc sông đó về điểm C cách B 144km. Thời gian tàu xuôi dòng ít hơn thời gian tàu ngược dòng là 30 phút. Tính vận tốc riêng của tàu và vận tốc dòng nước.

Bài 2: Một ô to dự định đi quãng đường AB với vận tốc không đổi. Khi đi được một nửa quãng đường, ô tô dừng lại vì bị chặn bởi tàu hỏa mất 3 phút. Vì vậy, để đến B đúng thời gian quy định ô tô phải tăng vận tốc thêm 2km/h trên quãng đường còn lại. Tính vận tốc dự định của ô tô.

Bài 3. Một ôtô dự định đi từ Lạng Sơn đến Hà Nội trong 4 giờ. Nhưng khi đi vì thấy đường thoáng và dễ đi nên ôtô đã tăng vận tốc thêm 10 km/h, do đó đã về Hà Nội sớm hơn dự định 48 phút. Tính vận tốc dự định của ôtô?

Bài 4: Một người đi xe đạp từ A đến B với vận tốc không đổi, hai địa điểm cách nhau 30km. Khi từ B về A người đó chọn đường khác dễ đi hơn nhưng dài hơn con đường cũ 6km. Vì vậy lúc về người đó đi với vận tốc lớn hơn lúc đi là 3km/h. Nên thời gian về vẫn ít hơn thời gian đi 3km. Tính vận tốc ban đầu của người đó.

Bài 5. Một người đi xe máy từ địa điểm X đến địa điểm Y với vận tốc 20 km/h. Lúc về người đó đi với vận tốc 30 km/h nên thời gian về ít hơn thời gian đi là 10 phút. Tính quãng đường XY.

Bài 6: Một ca nô đi tuần tra hết 5h với quãng đường xuôi dòng là 96km và ngược dòng là 48km. Một lần khác, ca nô đi xuôi dòng hết 48km và ngược dòng hết 60km trong 4h. Tính vận tốc riêng của nước và vận tốc riêng của ca nô.

Bài 7. Một người đi xe đạp dự định đi từ A đến B trong 2h. Do đường khó đi nên người đi xe đạp đã đi với vận tốc bé hơn vận tốc dự định 5 km/h và đã đến B muộn hơn so với dự định 1 giờ. Tìm vận tốc dự định?

Bài 8. Hai chiếc xe cùng khởi hành tại địa điểm A lúc 6 giờ sáng tới địa điểm B. Xe thứ nhất chạy với vận tốc 40 km/h, chậm hơn vận tốc của xe thứ hai 8 km/h. Lúc đi, xe thứ hai phải dừng 10 phút để sửa xe và hai xe tới B cùng một thời điểm. Tính chiều dài quãng đường AB.

Bài 9. Đường sông từ A đến B ngắn hơn đường bộ là 10 km. Ca nô đi từ A đến B mất 2 giờ 20 phút, ô tô đi hết 2 giờ. Vận tốc ca nô nhỏ hơn vận tốc ô tô là 17 km/h. Tính vận tốc của ô tô và ca nô?

Bài 10. Một tàu thủy chạy trên một khúc sông AB. Thời gian đi xuôi dòng từ A đến B là 3 giờ 20 phút, thời gian ngược dòng từ B về A là 5 giờ. Tính vận tốc của tàu thủy khi nước yên lặng? Biết rằng vận tốc dòng nước là 4 km/h.

Bài 11. Hai ôtô cùng khởi hành từ hai bến cách nhau 175 km để gặp nhau. Xe thứ nhất đi sớm hơn xe thứ hai là 1giờ 30 phút với vận tốc 30 km/h. Vận tốc của xe thứ hai là 35 km/h. Hỏi sau mấy giờ hai xe gặp nhau?

Bài 12. Lúc 6 giờ, một chiếc xe máy xuất phát từ A đến B với vận tốc trung bình 35km/h. Tại B, người lái xe làm nghỉ ngơi trong 10 phút rồi trở về A với vận tốc trung bình 40km/h và về đến A lúc 11 giờ cùng ngày. Tính quãng đường AB.

Bài 13. Từ hai địa điểm A và B cách nhau 36km, hai người đi xe đạp tới gặp nhau. Người thứ nhất xuất phát từ A, người thứ hai xuất phát từ B và có vận tốc lớn hơn người thứ nhất 4km/h. Hai xe gặp nhau sau 1 giờ rưỡi đạp xe. Tìm quãng đường mã mỗi người đã di chuyển khi gặp nhau.

Bài 14. Lúc 6 giờ sáng, một người lái xe máy từ A với vận tốc 40 km/h. Lúc 7 giờ, một người khác xuất phát từ B, cách A 50 km bắt đầu di chuyển cùng với hướng của xe thứ nhất với vận tốc 30 km/h. Cho rằng người thứ nhất phải đi qua B khi di chuyển. Hỏi hai xe gặp nhau lúc mấy giờ?

B. Lý thuyết Giải bài toán bằng cách lập hệ phương trình

Để giải một bài toán bằng cách lập hệ phương trình ta thực hiện qua ba bước sau:

Bước 1: Lập hệ phương trình:

- Chọn các ẩn số và đặt điều kiện, đơn vị thích hợp cho các ẩn số;

- Biểu diễn các đại lượng chưa biết theo các đại lượng đã biết;

- Lập hệ phương trình biểu diễn sự tương quan của các đại lượng.

Bước 2: Giải các hệ phương trình vừa tìm được.

Bước 3: Kiểm tra điều kiện ban đầu và kết luận bài toán.

Một số lưu ý:

- quãng đường = vận tốc  × thời gian

- vận tốc xuôi dòng = vận tốc khi nước yên lặng + vận tốc dòng nước

- vận tốc ngược dòng = vận tốc khi nước yên lặng - vận tốc dòng nước

Phương pháp giải: Vận dụng một số kiến thức về chuyển động sau:

- Với ba đại lượng tham gia là quãng đường (S); vận tốc (v); thời gian (t), ta có công thức liên hệ giữa ba đại lượng như sau:

S = vt

Với: S là quang đường có đơn vị là km; m…

v là vận tốc có đơn vị là km/h; m/s…

t là thời gian có đơn vị là h; s…

- Khi vật chuyển động trên dòng nước ta có:

$v_{xuoi}=v_{thuc}+v_{nuoc}$

$v_{nguoc}=v_{thuc}-v_{nuoc}$

Ví dụ 1: Một ô tô dự định đi từ A đến B trong một khoảng thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến sớm hơn dự định 3h. Nếu mỗi giờ xe chạy chậm hơn dự định 10km thì đến nơi chậm mất 5h. Tính vận tốc xe lúc đầu và thời gian dự định đi trên quãng đường AB.

Lời giải:

Gọi vận tốc dự định của ô tô là x (km/h) (x > 10)

Gọi thời gian dự định của ô tô là y (h) (y > 3)

Quãng đường AB là: S = xy (km) (1)

Nếu mỗi giờ ô tô tăng vận tốc 10 km/h thì vận tốc lúc đó là x + 10 (km/h)

Vì ô tô đến sớm hơn 3h nên thời gian đi hết quãng đường AB là y – 3 (h)

Quãng đường AB là: S = (x + 1)(y – 3) (km) (2)

Từ (1) và (2) ta có phương trình:

xy = (x + 10)(y – 3)

$\iff$xy = xy – 3x + 10y – 30

$\iff$3x – 10y = -30 (*)

Nếu mỗi giờ ô tô giảm vận tốc đi 10 km/h thì vận tốc lúc đó là x – 10 (km/h)

Vì ô tô đến muộn hơn 5h nên thời gian đi hết quãng đường AB là y + 5 (h)

Quang đường AB là: (x – 10)(y + 5) (km) (3)

Từ (1) và (3) ta có phương trình:

xy = (x – 10)(y + 5)

$\iff$xy = xy + 5x – 10y – 50

$\iff$5x – 10y = 50 (**)

Từ (*) và (**) ta có hệ phương trình

$\left\{\begin{array}{l}3x-10y=-30\text{ (4)}\\ 5x-10y=50\text{ (5)}\end{array}\right.$

Lấy (5) – (4) ta được:

$\iff \left\{\begin{array}{l}\left(5x-10y\right)-\left(3x-10y\right)=50+30\\ 3x-10y=-30\end{array}\right.$

$\iff \left\{\begin{array}{l}5x-10y-3x+10y=80\\ 3x-10y=-30\end{array}\right.$

$\iff \left\{\begin{array}{l}2x=80\\ 3x-10y=-30\end{array}\right.$

$\iff \left\{\begin{array}{l}x=80:2\\ 3x-10y=-30\end{array}\right.$

$\iff \left\{\begin{array}{l}x=40\\ 3.40-10y=-30\end{array}\right.$

$\iff \left\{\begin{array}{l}x=40\\ 10y=120+30\end{array}\right.$

$\iff \left\{\begin{array}{l}x=40\\ 10y=150\end{array}\right.$

$\iff \left\{\begin{array}{l}x=40\\ y=15\end{array}\right.$ (thỏa mãn)

Vậy vận tốc dự định của ô tô là 40 km/h và thời gian dự định của ô tô đi hết quãng đường AB là 15h.

Ví dụ 2: Một ca nô chạy trên một dòng sông trong 7h, biết chạy xuôi dòng là 108km và ngược dòng là 63km. Một lần khác ca nô cũng chạy trong 7h nhưng chạy xuôi dòng là 81km và chạy ngược dòng là 84km. Tính vận tốc nước chảy và vận tốc thực của ca nô.

Lời giải:

Gọi vận tốc thực của ca nô là x (km/h); vận tốc của nước là y (km/h) (x > y > 0)

Vận tốc xuôi dòng của ca nô là x + y (km/h)

Vận tốc ngược dòng của ca nô là x – y (km/h).

Thời gian xuôi dòng 108km của ca nô là $\frac{108}{x+y}$(h)

Thời gian ngược dòng 63km của ca nô là $\frac{63}{x-y}$(h)

Vì tổng thời gian xuôi dòng và ngược dòng lần thứ nhất là 7h nên ta có phương trình:

$\frac{108}{x+y}$ + $\frac{63}{x-y}$ = 7 (1)

Thời gian xuôi dòng 81km của ca nô là $\frac{81}{x+y}$(h)

Thời gian ngược dòng 84km của ca nô là $\frac{84}{x-y}$(h)

Vì tổng thời gian xuôi dòng và ngược dòng lần thứ 2 là 7h nên ta có phương trình:

$\frac{81}{x+y}$ + $\frac{84}{x-y}$ = 7 (2)

Từ (1) và (2) ta có hệ phương trình:

$\left\{\begin{array}{l}\frac{108}{x+y}+\frac{63}{x-y}=7\\ \frac{81}{x+y}+\frac{84}{x-y}=7\end{array}\right.$

Đặt $\left\{\begin{array}{l}\frac{1}{x+y}=a\\ \frac{1}{x-y}=b\end{array}\right.$

Khi đó hệ phương trình trở thành

$\left\{\begin{array}{l}108a+63b=7\text{ (3)}\\ 81a+84b=7\text{ (4)}\end{array}\right.$

Nhân cả hai vế phương trình (3) với 3 và phương trình (4) với 4 ta được:

$\left\{\begin{array}{l}324a+189b=21\text{ (5)}\\ 324a+336b=28\text{ (6)}\end{array}\right.$

Lấy (6) – (5) ta được:

$\left\{\begin{array}{l}\left(324a+336b\right)-\left(324a+189b\right)=28-21\\ 324a+189b=21\end{array}\right.$

$\iff \left\{\begin{array}{l}324a+336b-324a-189b=7\\ 324a+189b=21\end{array}\right.$

$\iff \left\{\begin{array}{l}147b=7\\ 324a+189b=21\end{array}\right.$

$\iff \left\{\begin{array}{l}a=\frac{21-189b}{324}\\ b=\frac{1}{21}\end{array}\right.$

$\iff \left\{\begin{array}{l}a=\frac{21-189.\frac{1}{21}}{324}\\ b=\frac{1}{9}\end{array}\right.$

$\iff \left\{\begin{array}{l}a=\frac{1}{27}\\ b=\frac{1}{21}\end{array}\right.$$\Rightarrow \left\{\begin{array}{l}\frac{1}{x+y}=\frac{1}{27}\\ \frac{1}{x-y}=\frac{1}{21}\end{array}\right.$

$\iff \left\{\begin{array}{l}x+y=27\\ x-y=21\end{array}\right.$$\iff \left\{\begin{array}{l}2x=27+21\\ y=27-x\end{array}\right.$

$\iff \left\{\begin{array}{l}2x=48\\ y=27-x\end{array}\right.$$\iff \left\{\begin{array}{l}x=24\\ y=27-24\end{array}\right.\iff \left\{\begin{array}{l}x=24\\ y=3\end{array}\right.$ (thỏa mãn)

Vậy vận tốc thực của ca nô là 24 km/h và vận tốc dòng nước là 3 km/h.

Ví dụ 3: Một ô tô đi từ A đến B trong một thời gian nhất định. Nếu xe chạy với vận tốc 35km/h thì đến chậm mất 2 giờ. Nếu xe chạy với vận tốc 50km/h thì đến sớm hơn 1 giờ. Tính quãng đường AB và thời gian dự định lúc đầu

Giải

Gọi t là thời gian dự định lúc đầu ( t đơn vị là giờ, t > 1)

Nếu xe chạy với vận tốc 35km/h thì thời gian đi từ A đến B là: t + 2 (giờ)

⇒ quãng đường AB là: 35.(t + 2) km  (1)

Nếu xe chạy với vận tốc 50km/h thì thời gian đi tử A đến B là: t - 1 (giờ)

⇒ quãng đường AB là: 50.(t - 1) km (2)

Từ (1) và (2) ta có phương trình:

Vậy thời gian dự định ban đầu là 8(giờ) và quãng đường AB dài 35.(t + 2) = 35.10 = 350 (km)

Ví dụ 4: Một ca nô đi xuôi dòng từ A đến B hết 1 giờ 20 phút và ngược dòng từ B về A hết 2 giờ. Tính vận tốc riêng của ca nô, biết vận tốc dòng nước là 3km/h

Giải

Đổi 1 giờ 20 phút = 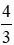 giờ

Gọi vận tốc riêng của ca nô là v ( v > 3)

Vận tốc của ca nô khi xuôi dòng là: v + 3 (km/h)

 quãng đường AB là: 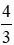(v + 3) km   (1)

Vận tốc của ca nô khi ngược dòng là: v - 3 (km/h)

 quãng đường AB là: 2(v - 3) km   (2)

Từ (1) và (2) ta có phương trình:

Vậy vận tốc riêng của ca nô là 15(km/h)