Với tóm tắt lý thuyết Toán lớp 10 Bài 1: Hàm số và đồ thị sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.
Lý thuyết Toán lớp 10 Bài 1: Hàm số và đồ thị
Video giải Toán 10 Bài 1: Hàm số và đồ thị - Cánh diều
A. Lý thuyết Hàm số và đồ thị
1. Hàm số
1.1. Định nghĩa
Cho tập hợp khác rỗng D ⊂ ℝ. Nếu với mỗi giá trị của x thuộc D có một và chỉ một giá trị tương ứng của y thuộc tập hợp số thực ℝ thì ta có một hàm số.
Ta gọi x là biến số và y là hàm số của x.
Tập D được gọi là tập xác định của hàm số.
Kí hiệu hàm số: y = f(x), x ∈ D.
Ví dụ:
a) Với hình tròn có bán kính r và đường kính d, ta có d = r. Như vậy d là hàm số của r vì mỗi giá trị của r chỉ cho đúng một giá trị của d.
b) Biểu thức y2 = x, như vậy ta thấy y không phải là hàm số của x vì khi x = 1 ta có hai giá trị của y là 1 và – 1.
1.2. Cách cho hàm số
a) Hàm số cho bằng một công thức
Hàm số được cho bằng biểu thức, cùng cách nói với hàm số cho bằng công thức.
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
Ví dụ:
a) Tìm tập xác định của hàm số y = .
Biểu thức có nghĩa khi x – 20 ⇔ x ≠ 2, vì vậy tập xác định của hàm số đã cho là: .
b) Tìm tập xác định của hàm số y =
Biểu thức có nghĩa khi x – 2 ≥ 0 ⇔ x ≥ 2, vì vậy tập xác định của hàm số đã cho là:.
b) Hàm số cho bằng nhiều công thức
Một hàm số có thể được cho bằng nhiều công thức.
Ví dụ:
Cho hàm số: f(x) =
a) Tìm tập xác định của hàm số trên?
b) Tính giá trị của hàm số khi x = – 5; x = 0; x = 2022.
Hướng dẫn giải:
a) Hàm số f(x) có nghĩa khi x < 0; x > 0; x = 0 nên tập xác định của hàm số là: D = ℝ
b) Với x = –5 < 0 thì f(–5) = –1;
Với x = 0 thì f(0) = 0;
Với x = 2022 > 1 thì f(2022) = 1.
Vậy giá trị của hàm số tại x = –5; x = 0; x = 2022 lần lượt là f(–5) = –1; f(0) = 0; f(2022) = 1.
Chú ý: Giả sử hàm số y = f(x) có tập xác định là D. Khi biến số x thay đổi trong tập D thì tập hợp các giá trị y tương ứng được gọi là tập giá trị của hàm số.
c) Hàm số không cho bằng công thức
Trong thực tiễn, có những tình huống dẫn tới những hàm số không thể cho bằng không thức (hoặc nhiều công thức).
Ví dụ: Biểu đồ lượng mưa tại Hà Nội trong năm 2021 (Đơn vị: mm)
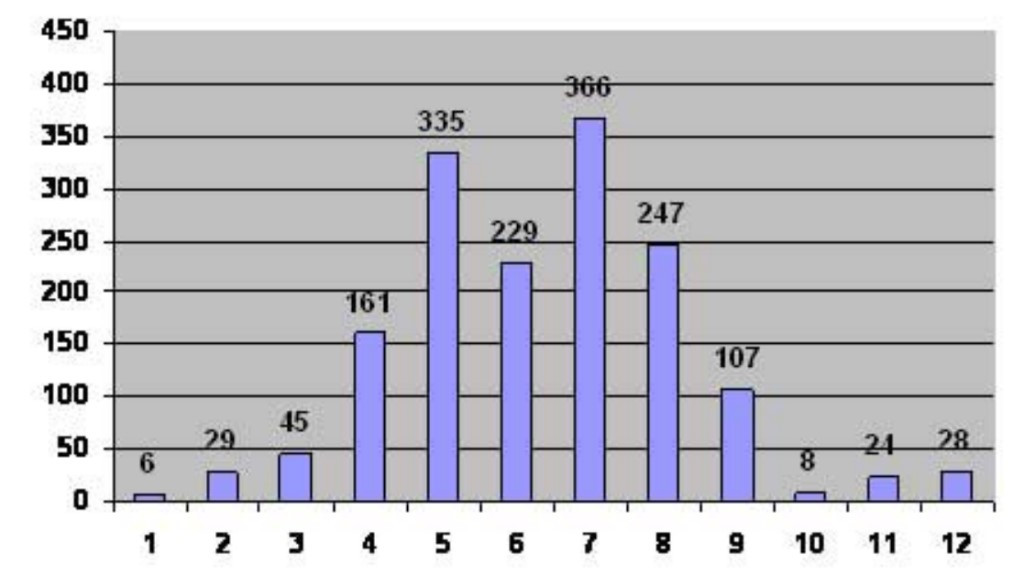
a) Xác định tập hợp các tháng được nêu trong biểu đồ.
b) Tương ứng tháng với lượng mưa trung bình của tháng đó có phải là hàm số không? Giải thích.
Giải:
a) Tập hợp các tháng là: D = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}
b) Mỗi tháng tương ứng xác định với đúng một giá trị của lượng mưa nên tương ứng đó xác định một hàm số. Hàm số đó có thể được cho bằng bảng như sau:
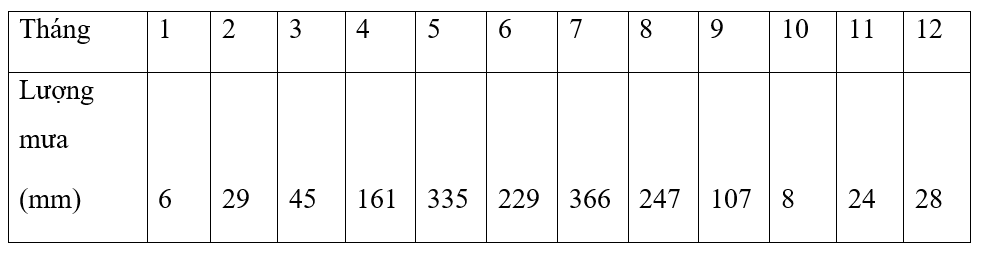
Đồ thị của hàm số y = f(x) xác định trên tập hợp D là tập hợp tất cả các điểm
M(x; f(x)) trong mặt phẳng toạ độ Oxy với mọi x thuộc D.
Ví dụ: Cho hàm số y = x + 3.
a) Vẽ đồ thị hàm số trên.
b) Trong mặt phẳng toạ độ Oxy cho ba điểm: A(0; 3); B(1;2); C(1; 1). Xác định điểm thuộc và không thuộc đồ thị trên.
Giải:
a) Khi x = 0 thay vào hàm số y = x + 3 ta được y = 3 như vậy đồ thị cắt trục Oy tại điểm (0;3).
Khi y = 0 thay vào hàm số y = x + 3 ta được x = –3 như vậy đồ thị cắt trục Ox tại điểm (–3; 0). Ta vẽ được đồ thị đi qua hai điểm trên.
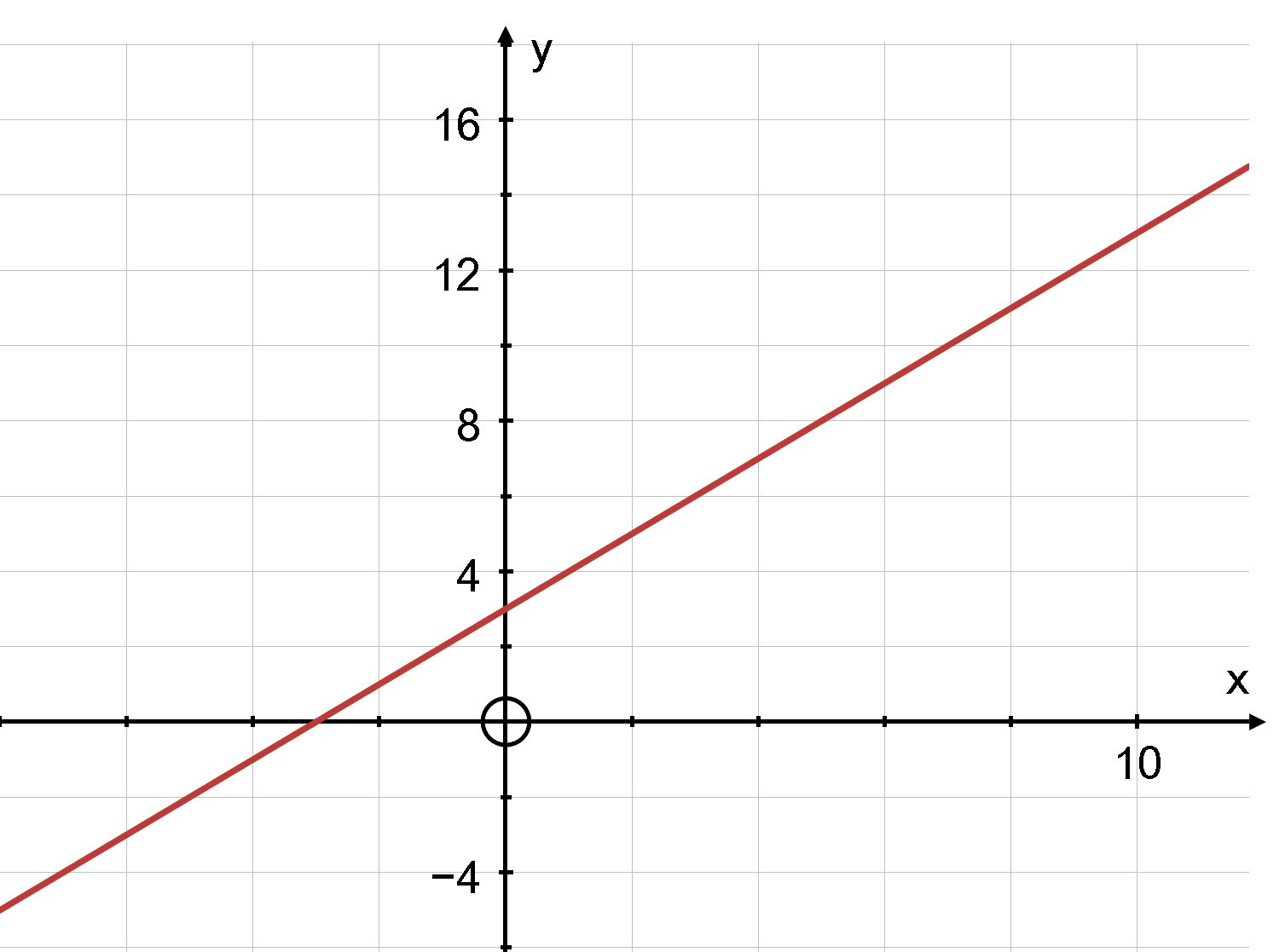
Đồ thị hàm số y = x + 3
b) Khi x = 0 thì y = 3; khi x = 1 thì y = 4. Vậy điểm điểm A(0; 3) thuộc đồ thị hàm số, điểm B(1; 2); C(1; 1) không thuộc đồ thị.
Chú ý:
– Điểm M(a; b) trong mặt phẳng toạ độ Oxy thuộc đồ thị hàm số y = f(x), x ∈ D khi và chỉ khi .
– Để chứng tỏ điểm M(a; b) trong mặt phẳng toạ độ không thuộc đồ thị hàm số
y = f(x), x ∈ D, ta có thể kiểm tra một trong hai khả năng sau:
Khả năng 1: Chứng tỏ rằng a ∉ D
Khả năng 2: Khi a ∈ D thì chứng tỏ rằng b ≠ f(a).
3. Sự biến của hàm số
Cho hàm số y = f(x) xác định trên khoảng (a; b):
– Hàm số y = f(x) gọi là đồng biến trên khoảng (a; b) nếu
– Hàm số y = f(x) gọi là nghịch biến trên khoảng (a; b) nếu
Ví dụ: Cho hàm số y = f(x) = x2
Xét sự biến thiên của hàm số trên khoảng (–∞; 0) và (0; +∞).
Hướng dẫn giải
+) Trên khoảng (–∞; 0) hàm số luôn xác định
Lấy x1, x2 ∈ (–∞; 0) thỏa mãn x1 < x2.
Vì x1 < x2 < 0 nên x12 > x22 hay f(x1) > f(x2)
Do đó hàm số nghịch biến trên (–∞; 0).
+) Trên khoảng (0; +∞) hàm số luôn xác định
Lấy x1, x2 ∈ (0; +∞) thỏa mãn x1 < x2.
Vì 0 < x1 < x2 nên x12 < x22 hay f(x1) < f(x2)
Do đó hàm số đồng biến trên (0; +∞).
Vậy hàm số đã cho nghịch biến trên (–∞; 0) và đồng biến trên (0; +∞).
Bảng biến thiên:
Đây là bảng thiên của hàm số y = x2.
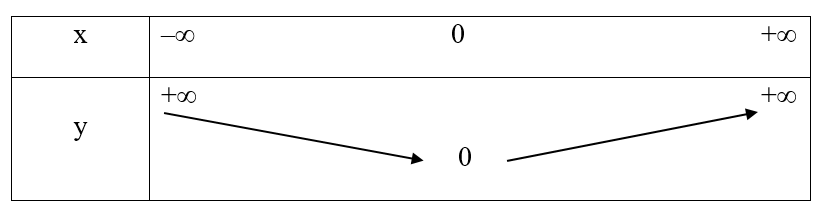
– Dấu mũi tên đi lên từ 0 đến +∞ diễn ta hàm số đồng biến trên khoảng (0; +∞).
Đồ thị hàm số:
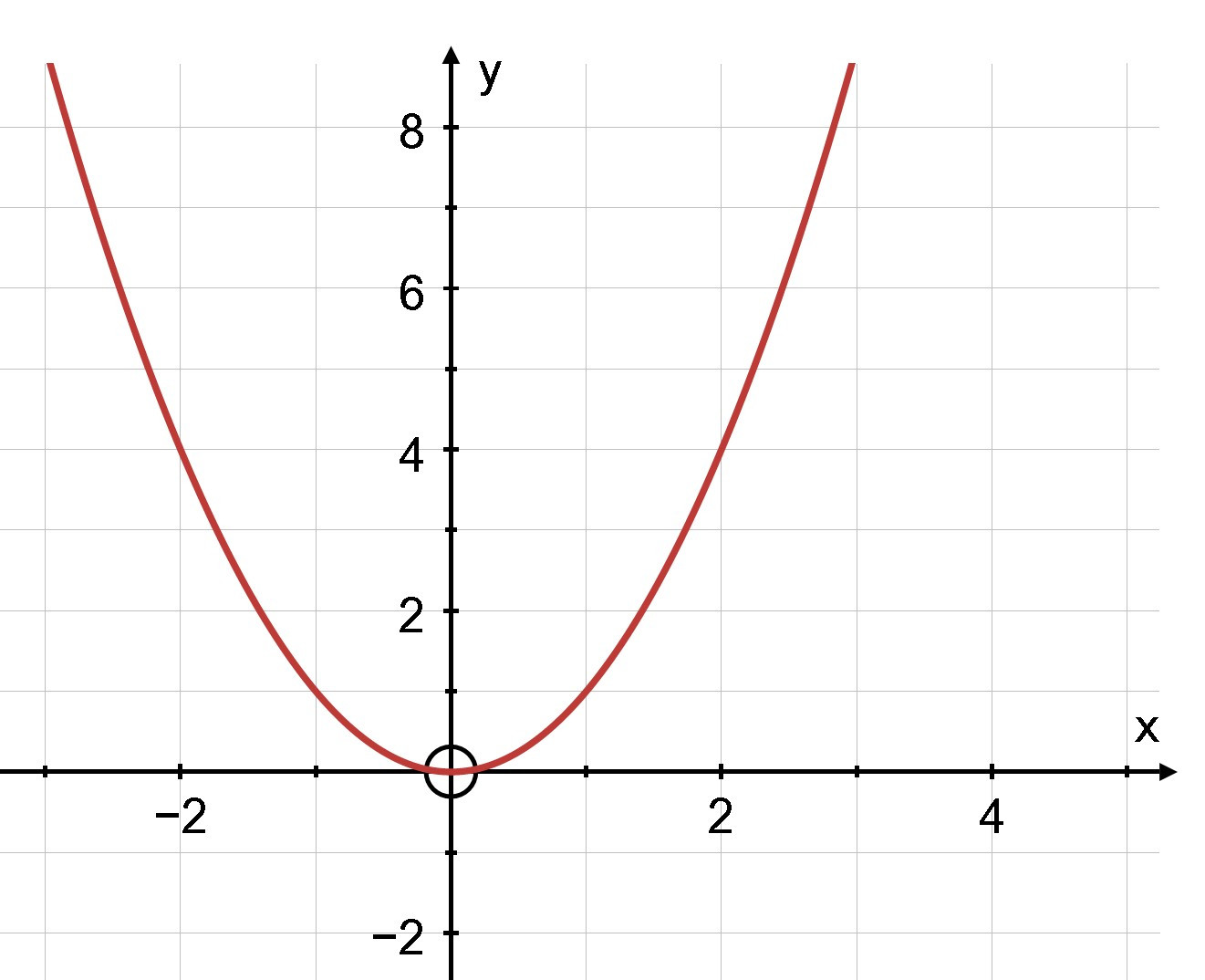
– Ta thấy hàm số nghịch biến trên khoảng (–∞; 0) khi đồ thị hàm số trên khoảng đó “đi xuống”.
– Hàm số đồng biến trên khoảng (0; +∞) khi đồ thị hàm số trên khoảng đó “đi lên”.
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1. Cho đồ thị hàm số y = f(x) như hình.
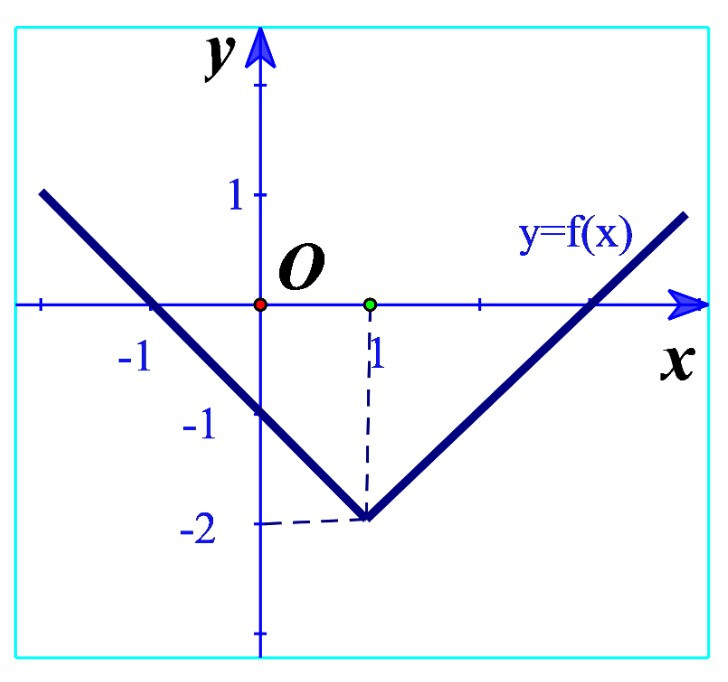
a) Trong các điểm có toạ độ (1; –2); (0; 0); (2; –1) điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?
b) Xác định f(0); f(3).
c) Tìm điểm thuộc đồ thị có tung độ bằng 0.
Hướng dẫn giải
a) Ta xác định các điểm A, O, B tương ứng với tọa độ (1; –2); (0; 0); (2; –1) trên hình:
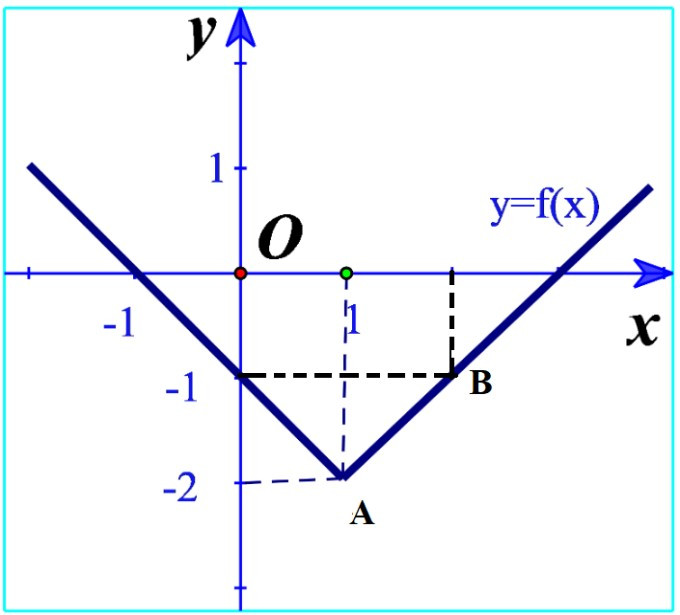
Quan sát đồ thị ta thấy điểm A có hoành độ bằng 1 và tung độ bằng –2 thuộc đồ thị của hàm số; Điểm B có hoành độ bằng 2 và tung độ bằng –1 thuộc đồ thị của hàm số; Điểm (0; 0) không thuộc đồ thị hàm số.
b)
– Giá trị của f(0) chính là giao điểm của đường thẳng x = 0 với đồ thị hàm số y = f(x). Quan sát đồ thị ta thấy giao điểm có hoành độ bằng –1 nên f(0) = –1
– Giá trị của f(3) chính là giao điểm của đường thẳng x = 3 với đồ thị hàm số y = f(x). Quan sát đồ thị ta thấy đường thẳng x = 3 song song với Oy nên f(3) = 0
Vậy f(0) = –1 và f(3) = 0.
c) Điểm thuộc đồ thị có tung độ bằng 0 chính là giao điểm của đường thẳng y = 0 và đồ thị. Quan sát đồ thị ta thấy có hai giao điểm với hoành độ là x = – 1 và x = 3.
Do đó ta có hai giao điểm của đồ thị và trục Ox là (–1; 0) và (3; 0).
Bài 2. Cho hàm số y = –2.x2
a) Điểm nào trong các điểm (−1; −2); (0; 0); (0; 1); (2021; 1) thuộc đồ thị của hàm số trên?
b) Tìm những điểm thuộc đồ thị hàm số có hoành độ lần lượt bằng −2; 3 và 10.
c) Tìm những điểm thuộc đồ thị hàm số có tung độ bằng −18.
Hướng dẫn giải
a)
– Thay toạ độ (–1; –2) vào hàm số y = –2.x2 ta được: –2 = –2. (– 1)2 (Đúng). Như vậy, điểm (–1; –2) thuộc đồ thị.
– Thay toạ độ (0; 0) vào hàm số y = –2.x2 ta được: 0 = –2.02 (Đúng). Như vậy điểm (0; 0) thuộc đồ thị.
– Thay toạ độ (0;1) vào hàm số y = –2.x2 ta được: 1 = –2.02 = 0 (Sai). Như vậy điểm (0; 1) không thuộc đồ thị.
– Thay điểm toạ độ (2021; 1) vào hàm số y = –2.x2 ta được: 1 = –2.20212 (Sai). Như vậy điểm (2021; 1) không thuộc đồ thị.
b)
– Thay x = –2 vào hàm số y = –2.x2, ta được: y = –2.(– 2)2 = –8. Khi đó ta được điểm có tọa độ (–2; –8).
– Thay x = 3 vào hàm số y = –2.x2, ta được: y = –2.32 = –18. Khi đó ta được điểm có tọa độ (3; –18).
– Thay x = 10 vào hàm số y = –2.x2, ta được: y = –2.102 = –200. Khi đó ta được điểm có tọa độ (10; –200).
Vậy những điểm cần tìm là: (–2; –8); (3; –18) và (10; –200).
c) Thay y = –18 vào hàm số y = –2.x2, ta được: –18 = –2.x2 ⇔ x2 = 9 ⇔ x = ±3. Khi đó ta được hai điểm có tọa độ (3; –18) và (–3; –18).
Vậy tọa độ những điểm cần tìm là (3; –18) và (–3; –18).
Bài 3. Tìm tập xác định của mỗi hàm số sau:
a) y = – x2;
b) y = ;
c) y = ;
d) y= .
Hướng dẫn giải
a) Tập xác định D = ℝ.
b) Biểu thức có nghĩa khi 2 – 3x ≥ 0 ⇔ x ≤ . Vì vậy tập xác định của hàm số: .
c) Biểu thức y = có nghĩa khi x + 1 ≠ 0 ⇔ x ≠ – 1. Vì vậy tập xác định của hàm số: .
d) Ta thấy hàm số có nghĩa với mọi x ∈ ℚ và x ∈ ℝ \ ℚ nên tập xác định của hàm số là: D = ℝ.
B.2 Bài tập trắc nghiệm
Câu 1. Cho hàm số y = f(x) = |5x|. Khẳng định nào sau đây là đúng?
A. f(2) = 10;
B. f(– 1) = 10;
C. f(– 2) = 1;
D. f(1) = 10.
Hướng dẫn giải
Đáp án đúng là: A
Thay lần lượt các giá trị: 2; –1; – 2; 1 vào biểu thức |5x| để được giá trị thỏa mãn.
Ta được: Khi x = 2 thay vào hàm số y: |5 . 2| = |10| = 10. (Chọn A)
Câu 2. Tìm tập xác định của y = .
A. D = (1; 2);
B. D = [1; 2];
C. D = [1; 3];
D. D = [– 1; 2];
Hướng dẫn giải
Đáp án đúng là: B
Để hàm số y xác định thì .
Tập xác định: D = [1; 2].
Câu 3. Xét sự biến thiên của hàm số y = trên khoảng (0; +∞). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên (0; +∞);
B. Hàm số nghịch biến trên (0; +∞);
C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng (0; +∞);
D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng (0; +∞).
Hướng dẫn giải
Đáp án đúng là: B
Với . Ta có:
Với mọi (0; +∞) và ta có: > 0 và x1 – x2 < 0.
Do đó, f(x1) – f(x2) = > 0 ⇔ f(x1) > f(x2).
Hàm số y = nghịch biến trên (0; +∞).
Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Lý thuyết Bài 1: Hàm số và đồ thị
Lý thuyết Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Lý thuyết Bài 3: Dấu của tam thức bậc hai
Lý thuyết Bài 4: Bất phương trình bậc hai một ẩn
Bài giảng Toán 10 Bài 1: Hàm số và đồ thị - Cánh diều