Với tóm tắt lý thuyết Toán lớp 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.
Lý thuyết Toán lớp 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Video giải Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn - Cánh diều
A. Lý thuyết Hệ bất phương trình bậc nhất hai ẩn
1. Hệ bất phương trình bậc nhất hai ẩn
• Hệ bất phương trình bậc nhất hai ẩn x, y là một hệ gồm một số bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung của các bất phương trình trong hệ được gọi là một nghiệm của hệ bất phương trình đó.
Ví dụ: Cho hệ bất phương trình sau: .
Cặp số (x ; y) nào trong các cặp (3; 1), (– 1; 0), (4; – 1) là nghiệm của hệ bất phương trình trên?
Hướng dẫn giải:
+ Thay x = 3, y = 1 vào hai bất phương trình của hệ, ta có:
2 . 3 + 1 = 7 > 0 là mệnh đề đúng;
3 – 3 . 1 = 0 < 6 là mệnh đề đúng.
Vậy (3; 1) là nghiệm chung của (1) và (2), do đó là nghiệm của hệ bất phương trình.
+ Thay x = – 1, y = 0 vào bất phương trình (1), ta có:
2 . (– 1) + 0 = –2 > 0 là mệnh đề sai;
(– 1) – 3 . 0 = –1 < 6 là mệnh đề đúng.
Vậy (– 1; 0) không là nghiệm của (1), do đó không phải nghiệm của hệ bất phương trình.
+ Thay x = 4, y = –1 vào bất phương trình (2) của hệ, ta có:
2 . 4 + (– 1) = 7 > 0 là mệnh đề đúng;
4 – 3 . (– 1) = 7 < 6 là mệnh đề sai.
Vậy (4 ; – 1) không là nghiệm của (2), do đó không phải nghiệm của hệ bất phương trình.
2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
• Miền nghiệm của hệ bất phương trình là giao của các miền nghiệm của các bất phương trình trong hệ.
• Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn, ta làm như sau:
+ Trong cùng mặt phẳng toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
+ Phần không bị gạch là miền nghiệm cần tìm.
Ví dụ: Biểu diễn trên mặt phẳng Oxy miền nghiệm của hệ bất phương trình:
.
Hướng dẫn giải
+ Vẽ 3 đường thẳng
d1: x + y = –2,
d2: x – y = 1
d3: 2x – y = –1.
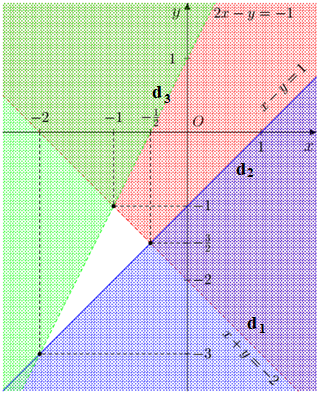
+ Toạ độ điểm (0; 0) là nghiệm của các bất phương trình (2) và (3), không phải nghiệm của bất phương trình (1).
Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là miền không bị gạch kể cả đường thẳng d2 và không kể đường thẳng d1 và d3.
3. Áp dụng vào bài toán thực tiễn
Bài toán. Một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hoà: điều hoà hai chiều và điều hoà một chiều, với số vốn ban đầu không quá 1,2 tỉ đồng.
|
|
Điều hoà hai chiều |
Điều hoà một chiều |
|
Giá mua vào |
20 triệu đồng / 1 máy |
10 triệu đồng / 1 máy |
|
Lợi nhuận dự kiến |
3,5 triệu đồng / 1 máy |
2 triệu đồng / 1 máy |
Cửa hàng ước tính rằng tổng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Nếu là chủ cửa hàng, em cần đầu tư kinh doanh mỗi loại bao nhiêu máy để lợi nhuận thu được là lớn nhất?
Hướng dẫn giải
Giả sử cửa hàng nhập về x máy điều hoà hai chiều và y máy điều hoà một chiều (x ≥ 0, y ≥ 0 và x, y ∈ ℕ*).
Vì nhu của thị trường không quá 100 máy cả hai loại nên x + y ≤ 100.
Số tiền để nhập hai loại máy điều hoà với số lượng như trên là: 20x + 10y (triệu đồng).
Số tiền đầu tư tối đa là 1,2 tỉ đồng = 1 200 triệu đồng nên ta có 20x + 10y ≤ 1200 hay 2x + y ≤ 120.
Từ đó thu được hệ bất phương trình: với x, y ∈ ℕ*.
Lợi nhuận thu được khi bán x máy điều hoà hai chiều và y máy điều hoà một chiều là:
T = 3,5x + 2y (triệu đồng).
Bài toán được đưa về: Tìm giá trị x, y thoả mãn hệ bất phương trình (I) sao cho T đạt giá trị lớn nhất.
Trước hết, ta xác định miền nghiệm của hệ bất phương trình (I) là miền tứ giác OABC với toạ độ các đỉnh O(0 ; 0), A(0 ; 100), B(20 ; 80), C(60 ; 0).
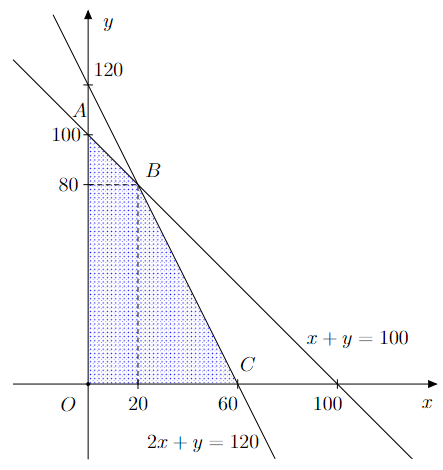
Người ta chứng minh được: Biểu thức T = 3,5x + 2y đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác OABC.
Lần lượt thay toạ độ các điểm O, A, B, C vào biểu thức T, ta được:
Với x = 0, y = 0 thì T = 3,5.0 + 2.0 = 0;
Với x = 0, y = 100 thì T = 3,5.0 + 2.100 = 200;
Với x = 20, y = 80 thì T = 3,5.20 + 2.80 = 230;
Với x = 60, y = 0 thì T = 3,5.60 + 2.0 = 21.
Ta thấy giá trị lớn nhất là T = 230 khi x = 20 và y = 80.
Vậy cửa hàng cần đầu tư 20 máy điều hoà hai chiều và 80 máy điều hoà một chiều để thu được lợi nhuận lớn nhất.
• Tổng quát: Giá trị lớn nhất (hoặc nhỏ nhất) của biểu thức bậc nhất F(x , y) = ax + by trong miền đa giác A1A2…An là giá trị của F(x , y) tại một trong các đỉnh của đa giác đó.
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1. Biểu diễn miền nghiệm của các hệ bất phương trình sau: .
Hướng dẫn giải:
Ta có hệ bất phương trình được biến đổi thành hệ: .
Dựng các đường thẳng:
d1: 3x + 2y = 0;
d2: 2x + 3y = 6;
d3: 2x – 3y =2.
Do tọa độ điểm (1; 1) thỏa mãn các bất phương trình trong hệ nên miền nghiệm của từng bất phương trình trong hệ lần lượt là những nửa mặt phẳng không bị gạch chứa điểm (1; 1) kể cả đường thẳng d1, d3 và không kể đường thẳng d2.
Miền nghiệm của hệ là miền không bị gạch trong hình dưới.
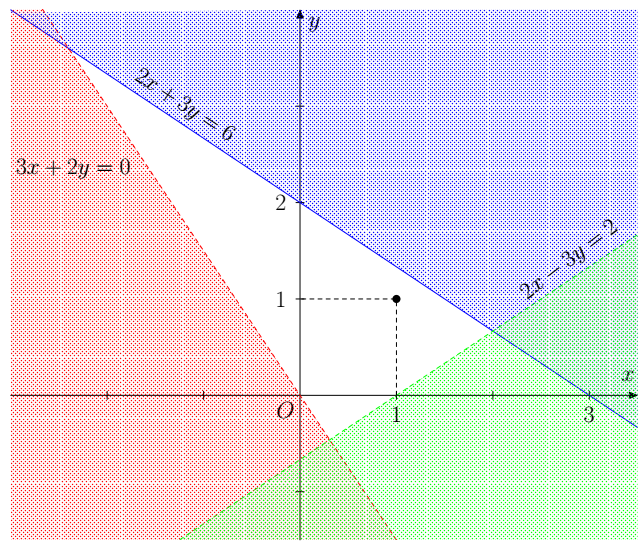
Bài 2. Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B có giá lần lượt là 10 triệu đồng và 20 triệu đồng, với số vốn ban đầu không quá 4 tỉ đồng. Lãi thu về khi bán mỗi máy loại A là 2,5 triệu đồng, mỗi máy loại B là 4 triệu đồng. Cửa hàng ước tính nhu cầu tiêu thụ không quá 250 máy. Tìm số lượng máy tính mỗi loại mà cửa hàng cần nhập về để lợi nhuận thu được là lớn nhất.
Hướng dẫn giải:
Gọi số máy mỗi loại A, B cần nhập về lần lượt là x, y (x ≥ 0, y ≥ 0 và ).
Do nhu cầu không quá 250 máy nên x + y ≤ 250.
Số vốn bỏ ra để nhập máy về là 10x + 20y (triệu đồng).
Ta có 4 tỉ đồng = 4 000 triệu đồng.
Vì số vốn không quá 4 tỉ nên 10x + 20y ≤ 4 000 hay x + 2y ≤ 400.
Lãi thu về khi bán hết hàng là T = 2,5x + 4y (triệu đồng).
Ta cần tìm x, y thoả mãn hệ bất phương trình với .
sao cho T = 2,5x + 4y đạt giá trị lớn nhất.
Miền nghiệm của hệ bất phương trình được biểu diễn bởi miền tứ giác OABC với O(0 ; 0), A(0 ; 200), B(100 ; 150), C(250 ; 0).
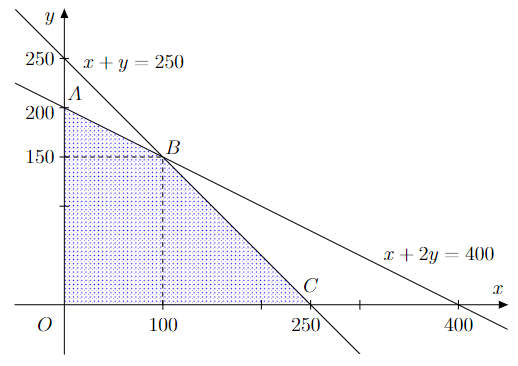
Xét giá trị của T tại các đỉnh của tứ giác, ta có:
Tại O(0 ; 0), với x = 0 và y = 0 thì T = 2,5.0 + 4.0 = 0;
Tại A(0; 200), với x = 0 và y = 200 thì T = 2,5.0 + 4.200 = 800;
Tại B(100; 150), với x = 100 và y = 150 thì T = 2,5.100 + 4.150 = 850;
Tại C(250; 0), với x = 250 và y = 0 thì T = 2,5.250 + 4.0 = 625.
Suy ra giá trị lớn nhất là T = 850 đạt được khi x = 100, y = 150 (toạ độ điểm B).
Vậy cửa hàng cần nhập 100 máy loại A và 150 máy loại B để đạt lợi nhuận lớn nhất.
Bài 3. Một hộ dân dự định dùng tối đa 8 ha rừng để trồng cây keo và cây bạch đàn. Nếu trồng keo thì mỗi ha cần 20 công và thu về 300 triệu đồng, nếu trồng bạch đàn thì mỗi ha cần 30 công và thu về 400 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được lãi cao nhất, với tổng số công không quá 180?
Hướng dẫn giải:
Gọi x (ha) là diện tích trồng keo, y (ha) là diện tích trồng bạch đàn.
Điều kiện x ≥ 0, y ≥ 0.
Tổng diện tích không quá 8 ha, tức là x + y ≤ 8 (ha).
Số công cần cho x ha keo là 20x (công)
Số công cần cho y ha bạch đàn là 30y (công)
Vì tổng số công không quá 180 nên ta có bất phương trình 20x + 30y ≤ 180 hay 2x + 3y ≤ 18.
Số tiền thu được là T = 300x + 400y (triệu đồng).
Ta cần tìm x, y thoả mãn hệ bất phương trình
sao cho T = 300x + 400y đạt giá trị lớn nhất.
Miền nghiệm của hệ bất phương trình được biểu diễn bởi miền tứ giác OABC với O(0 ; 0), A(0 ; 6), B(6 ; 2), C(8 ; 0).
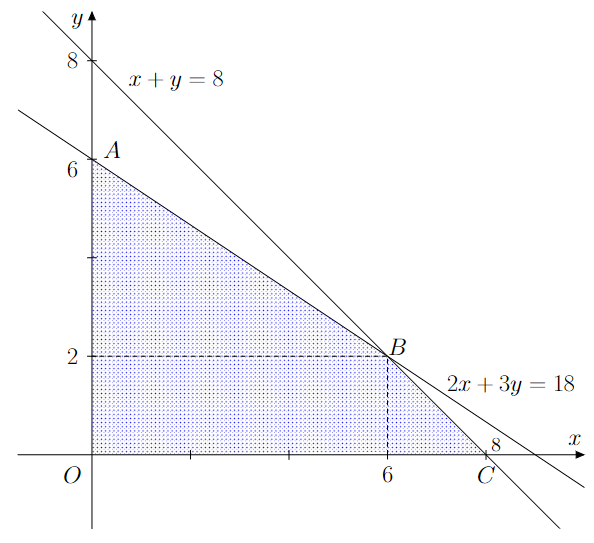
Xét giá trị của T tại các đỉnh của tứ giác, ta có:
Tại O(0 ; 0), với x = 0 và y = 0 thì T = 300.0 + 400.0 = 0;
Tại A(0 ; 6), với x = 0 và y = 6 thì T = 300.0 + 400.6 = 2 400;
Tại B(6 ; 2), với x = 6 và y = 2 thì T = 300.6 + 400.2 = 2 600;
Tại C(8 ; 0), với x = 8 và y = 0 thì T = 300.8 + 400.0 = 2 400.
Suy ra giá trị lớn nhất là T = 2 600 khi x = 6, y = 2 (toạ độ điểm B).
Vậy cần trồng 6 ha keo và 2 ha bạch đàn để thu được lợi nhuận lớn nhất.
B.2 Bài tập trắc nghiệm
Câu 1. Phần không bị gạch ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D (không kể bờ) ?
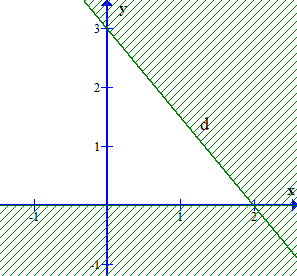
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là: A
Giả sử đường thẳng d có phương trình d: y = ax + b
Dễ thấy đường thẳng d đi qua hai điểm (0; 3) và (2; 0). Ta có hệ
.
Vậy phương trình đường thẳng d: y = x + 3 ⇔ 3x +2y = 6
Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 3.0 + 2.0 = 0 < 6. Mà điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy bất phương trình có dạng 3x + 2y < 6.
Miền nghiệm là nửa mặt phẳng nằm phía trên trục hoành: y > 0
Vậy phần không bị gạch trong hình vẽ biểu diễn miền nghiệm của hệ bất phương trình .
Câu 2. Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình là
A. (0; 0);
B. (1; 1);
C. (– 1; 1);
D. (– 1; – 1).
Hướng dẫn giải
Đáp án đúng là: C
Xét đáp án A ta có: đáp án A thoả mãn hệ bất phương trình
Xét đáp án B ta có : đáp án B thoả mãn hệ bất phương trình
Xét đáp án C ta có : đáp án C không thoả mãn hệ bất phương trình
Xét đáp án D ta có : đáp án D thoả mãn hệ bất phương trình
Vậy đáp án đúng là C.
Câu 3. Điểm O(0; 0) thuộc miền nghiệm của hệ bất phương trình nào sau đây?
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là: C
Thay x = 0, y = 0 vào từng đáp án ta được:
Xét đáp án A: . Vậy điểm O(0 ; 0) không thoả mãn hệ bất phương trình. Đáp án A sai
Xét đáp án B: . Vậy điểm O(0 ; 0) không thoả mãn hệ bất phương trình. Đáp án B sai
Xét đáp án C: . Vậy điểm O(0 ; 0) thoả mãn hệ bất phương trình. Đáp án C đúng.
Xét đáp án D : . Vậy điểm O(0 ; 0) không thoả mãn hệ bất phương trình.
Đáp án D sai.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 1: Bất phương trình bậc nhất hai ẩn
Lý thuyết Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Lý thuyết Bài 1: Hàm số và đồ thị
Lý thuyết Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Lý thuyết Bài 3: Dấu của tam thức bậc hai
Bài giảng Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn - Cánh diều