Tài liệu chuyên đề Phương pháp tọa độ trong mặt phẳng Toán lớp 10 sách Cánh diều gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Cánh diều word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Phương pháp tọa độ trong mặt phẳng

Tài liệu gồm 8 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Tọa độ của vectơ:

Chuyên đề 2: TỌA ĐỘ CỦA VECTƠ

Nhắc lại hệ tọa độ: Hệ trục tọa độ \[\left( {O;\vec i,\vec j} \right)\] gồm hai trục \[\left( {O;\vec i} \right)\] và \[\left( {O;\vec j} \right)\] vuông góc với nhau.

Điểm gốc \[O\] chung của hai trục gọi là gốc tọa độ. Trục \[\left( {O;\vec i} \right)\] được gọi là trục hoành và kí

hiệu là \[Ox,\] trục \[\left( {O;\vec j} \right)\] được gọi là trục tung và kí hiệu là \[Oy.\] Các vectơ \[\vec i\] và \[\vec j\] là các vectơ

đơn vị trên \[Ox\]và \[Oy\] và \[\left| {\vec i} \right| = \left| {\vec j} \right| = 1.\] Hệ trục tọa độ \[\left( {O;\vec i,\vec j} \right)\] còn được kí hiệu là \[Oxy.\]

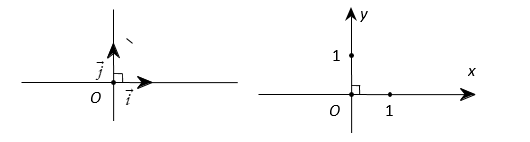
Mặt phẳng mà trên đó đã cho một hệ trục tọa độ \[Oxy\] còn được gọi là mặt phẳng tọa độ \[Oxy\]

Hay gọi tắt là mặt phẳng \[Oxy.\]

I. TỌA ĐỘ CỦA MỘT ĐIỂM

Trong mặt phẳng tọa độ \[Oxy\] cho một điểm \[M\] tùy ý.

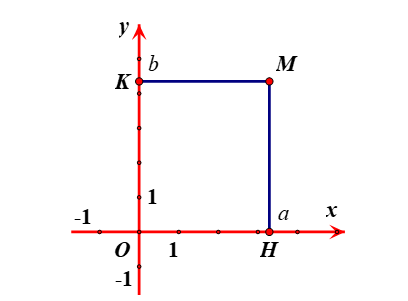
Từ \(M\) kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm \(H\) ứng với số \(a\). Số \(a\) là hoành độ của điểm \(M\).

Từ \(M\) kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm \(K\) ứng với số \(b\). Số \(b\) là tung độ của điểm \(M\).

Cặp số \(\left( {a;b} \right)\) là tọa độ của điểm \(M\) trong mặt phẳng tọa độ \(Oxy\). Ta kí hiệu là \(M\left( {a;b} \right)\).

I. TỌA ĐỘ VECTƠ

Tọa độ của điểm \(M\) là tọa độ của vectơ \(\overrightarrow {OM} \).

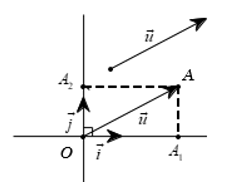
Trong mặt phẳng \[Oxy\] cho một vectơ \[\vec u\] tùy ý. Vẽ $\overrightarrow{OA}=\overrightarrow{u}$. Với mỗi vectơ \[\vec u\] ta xác định được duy nhất một điểm \[A\] sao cho $\overrightarrow{OA}=\overrightarrow{u}$

Với mỗi vectơ \[\vec u\] trong mặt phẳng tọa độ \[Oxy\], tọa độ của \[\vec u\] là tọa độ của điểm \[A\] sao cho $\overrightarrow{OA}=\overrightarrow{u}$

Trong mặt phẳng tọa độ \[Oxy\], nếu \[\vec u = \left( {x;y} \right)\] thì \[\vec u = x\,\vec i + y\,\vec j\,\]. Ngược lại nếu \[\vec u = x\,\vec i + y\,\vec j\,\] thì \[\vec u = \left( {x;y} \right)\]

Do đó: $\overrightarrow{u}=(x;y)\iff \overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}$

Nhận xét. Từ định nghĩa tọa độ của vectơ, ta thấy hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

Nếu \[\vec u = \left( {x;y} \right)\] và $\overrightarrow{u^{\text{'}}}=(x^{\text{'}};y^{\text{'}})$ thì $\overrightarrow{u}=\overrightarrow{u^{\text{'}}}\iff \{\begin{array}{c}x=x^{\text{'}}\text{y}=y^{\text{'}}\end{array}$

Như vậy, mỗi vectơ được hoàn toàn xác định khi biết tọa độ của nó.

III. LIÊN HỆ GIỮA TOẠ ĐỘ CỦA ĐIỂM VÀ TOẠ ĐỘ CỦA VECTƠ

Cho \(A({x_A};{y_A}),{\rm{ }}B({x_B};{y_B})\) thì $\overrightarrow{AB}=(x_B-x_A;y_B-y_A)$

IV. BIỂU THỨC TỌA ĐỘ CỦA PHÉP TOÁN VECTƠ

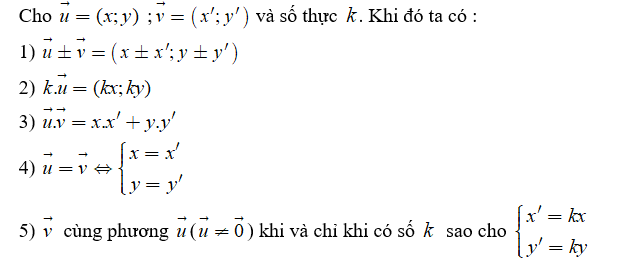
V. TỌA ĐỘ TRUNG ĐIỂM CỦA ĐOẠN THẲNG. TỌA ĐỘ TRỌNG TÂM CỦA TAM GIÁC

Cho đoạn thẳng \(AB\) có \(A\left( {{x_A};{y_A}} \right),{\mkern 1mu} {\mkern 1mu} B\left( {{x_B};{y_B}} \right).\) Ta dễ dàng chứng minh được tọa độ trung điểm

\(I\left( {{x_I};{y_I}} \right)\) của đoạn thẳng \(AB\) là

$x_I=\frac{x_A+x_B}{2},y_I=\frac{y_A+y_B}{2}.$

Cho tam giác \[ABC\] có \[A\left( {{x_A};{y_A}} \right),\,\,B\left( {{x_B};{y_B}} \right),\,\,C\left( {{x_C};{y_C}} \right).\] Khi đó tọa độ của trọng tâm

\[G\left( {{x_G};{y_G}} \right)\]của tam giác \[ABC\] được tính theo công thức

$x_G=\frac{x_A+x_B+x_C}{3},y_G=\frac{y_A+y_B+y_C}{3}.$

VI. BIỂU THỨC TỌA ĐỘ CỦA TÍCH VÔ HƯỚNG

Trên mặt phẳng tọa độ \(Oxy\), cho hai vectơ$\overrightarrow{a}=(a_1;a_2),\overrightarrow{b}=(b_1;b_2)$

Khi đó $\overrightarrow{a}.\overrightarrow{b}=a_1.b_1+a_2.b_2$

Ứng dụng biểu thức tọa độ của các phép toán vecto

Trên mặt phẳng tọa độ \(Oxy\), cho hai vectơ $\overrightarrow{a}=(a_1;a_2),\overrightarrow{b}=(b_1;b_2)$ và hai điểm  $A(x_A;y_A),B(x_B;y_B).$

1) $\overrightarrow{a}\perp \overrightarrow{b}\iff \overrightarrow{a}.\overrightarrow{b}=0\iff a_1{b}_1+a_2{b}_2=0$

2) \(\overrightarrow a ,\overrightarrow b \) cùng phương \( \Leftrightarrow {a_1}{b_1} - {a_2}{b_2} = 0\)

3) \(\left| {\overrightarrow a } \right| = \sqrt {a_1^2 + a_2^2} \)

4) \[AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \]

5) $\cos (\overrightarrow{a};\overrightarrow{b})=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{a_1{b}_1+a_2{b}_2}{\sqrt{a_1^2+a_2^2}.\sqrt{b_1^2+b_2^2}}$ $\overrightarrow{a}=(a_1;a_2)$ $\overrightarrow{b}=(b_1;b_2)$