Tài liệu chuyên đề Bất phương trình bậc hai một ẩn Toán lớp 10 sách Chân trời sáng tạo gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Chân trời sáng tạo word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Bất phương trình bậc hai một ẩn

Tài liệu gồm 4 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Dấu của tam thức bậc hai :

Chuyên đề 2: DẤU CỦA TAM THỨC BẬC HAI

Câu 1:     Cho tam thức \(f\left( x \right) = a{x^2} + bx + c{\rm{    }}\left( {a \ne 0} \right),\) \(\Delta  = {b^2} - 4ac\). Ta có \(f\left( x \right) \le 0\) với \(\forall x \in \mathbb{R}\)khi và chỉ khi:

A. \(\left\{ \begin{array}{l}a < 0\\\Delta  \le 0\end{array} \right.\).     B. \(\left\{ \begin{array}{l}a \le 0\\\Delta  < 0\end{array} \right.\).          C. \(\left\{ \begin{array}{l}a < 0\\\Delta  \ge 0\end{array} \right.\).         D. \(\left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right.\).

Câu 2:     Cho tam thức bậc hai \(f(x) =  - 2{x^2} + 8x - 8\). Trong các mệnh đề sau, mệnh đề nào đúng?

A. \(f(x) < 0\) với mọi \(x \in \mathbb{R}\).      B. \(f(x) \ge 0\) với mọi \(x \in \mathbb{R}\).

C. \(f(x) \le 0\) với mọi \(x \in \mathbb{R}\).    D. \(f(x) > 0\) với mọi \(x \in \mathbb{R}\).

Câu 3:     Tam thức nào dưới đây luôn dương với mọi giá trị của \[x\]?

A. \({x^2} - 10x + 2\).    B. \({x^2} - 2x - 10\).   C. \({x^2} - 2x + 10\).  D. \( - {x^2} + 2x + 10\).

Câu 4:     Tìm khẳng định đúng trong các khẳng định sau?

A. \(f\left( x \right) = 3{x^2} + 2x - 5\) là tam thức bậc hai.                    B. \(f\left( x \right) = 2x - 4\) là tam thức bậc hai.

C. \(f\left( x \right) = 3{x^3} + 2x - 1\) là tam thức bậc hai.                    D. \(f\left( x \right) = {x^4} - {x^2} + 1\) là tam thức bậc hai.

Câu 5:     Cho \(f\left( x \right) = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) và \(\Delta  = {b^2} - 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\).

A. \(\Delta  < 0\).            B. \(\Delta  = 0\).         C. \(\Delta  > 0\).         D. \(\Delta  \ge 0\).

Câu 6:     Cho hàm số \(y = f\left( x \right) = a{x^2} + bx + c\) có đồ thị như hình vẽ. Đặt \(\Delta  = {b^2} - 4ac\), tìm dấu của \(a\) và \(\Delta \).

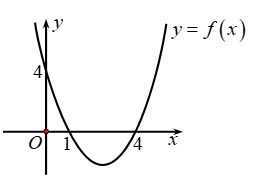
A. \(a > 0\), \(\Delta  > 0\).                                  B. \(a < 0\), \(\Delta  > 0\).                                        C. \(a > 0\), \(\Delta  = 0\).                                D. \(a < 0\), \(,{\rm{ }}\Delta  = 0\).

Câu 7:     Cho tam thức \(f\left( x \right) = {x^2} - 8{\rm{x}} + 16\). Khẳng định nào sau đây là đúng?

A. phương trình \(f\left( x \right) = 0\) vô nghiệm.                                  B. \(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\).

C. \(f\left( x \right) \ge 0\) với mọi \(x \in \mathbb{R}\).                       D. \(f\left( x \right) < 0\) khi \(x < 4\).

Câu 8:     Cho tam thức bậc hai \(f\left( x \right) = {x^2} + 1\). Mệnh đề nào sau đây đúng?

A. \(f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ; + \infty } \right)\).                         B. \(f\left( x \right) = 0 \Leftrightarrow x =  - 1\).

C. \(f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \infty ;1} \right)\).                                        D. \(f\left( x \right) > 0 \Leftrightarrow x \in \left( {0;1} \right)\).

Câu 9:     Cho tam thức bậc hai \[f(x) = a{x^2} + bx + c\,\,\,(a \ne 0)\]. Mệnh đề nào sau đây đúng?

A. Nếu\[\,\Delta  > 0\] thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\), với mọi \[x \in \mathbb{R}\].

B. Nếu\[\,\Delta  < 0\] thì \(f\left( x \right)\) luôn trái dấu với hệ số \(a\), với mọi \[x \in \mathbb{R}\].

C. Nếu\[\,\Delta  = 0\] thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\), với mọi \[x \in \mathbb{R}\backslash \left\{ { - \frac{b}{{2a}}} \right\}\].

D. Nếu\[\,\Delta  < 0\]thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(b\), với mọi \[x \in \mathbb{R}\].