Tài liệu chuyên đề Hàm số bậc hai và đồ thị Toán lớp 10 sách Chân trời sáng tạo gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Chân trời sáng tạo word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Hàm số bậc hai và đồ thị

Tài liệu gồm 2 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Hàm số bậc hai :

Chuyên đề 2: HÀM SỐ BẬC HAI

DẠNG 1. SỰ BIẾN THIÊN

Câu 1:         Hàm số \(y = a{x^2} + bx + c\), \((a > 0)\) đồng biến trong khoảng nào sau đậy?

A. \(\left( { - \infty ;\, - \frac{b}{{2a}}} \right).\)                                     B. \(\left( { - \frac{b}{{2a}};\, + \infty } \right).\)   C. \(\left( { - \frac{\Delta }{{4a}};\, + \infty } \right).\)                               D. \(\left( { - \infty ;\, - \frac{\Delta }{{4a}}} \right).\)

Lời giải

Chọn B

\(a > 0.\) Bảng biến thiên

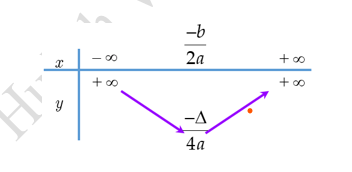
Câu 2:         Hàm số \(y = a{x^2} + bx + c\), \((a > 0)\) nghịch biến trong khoảng nào sau đậy?

A. \(\left( { - \infty ;\, - \frac{b}{{2a}}} \right).\)                                     B. \(\left( { - \frac{b}{{2a}};\, + \infty } \right).\)   C. \(\left( { - \frac{\Delta }{{4a}};\, + \infty } \right).\)                               D. \(\left( { - \infty ;\, - \frac{\Delta }{{4a}}} \right).\)

Lời giải

Chọn A

\(a > 0.\) Bảng biến thiên

Câu 3:         Cho hàm số \[y =  - {x^2} + 4x + 1\]. Khẳng định nào sau đây sai?

A. Trên khoảng \[\left( { - \infty ;1} \right)\] hàm số đồng biến.

B. Hàm số nghịch biến trên khoảng \[\left( {2; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;2} \right)\].

C. Trên khoảng \[\left( {3; + \infty } \right)\]hàm số nghịch biến.

D. Hàm số nghịch biến trên khoảng \[\left( {4; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;4} \right)\].

Lời giải

Chọn D

Đỉnh của parabol: \[{x_I} =  - \frac{b}{{2a}} = 2\]

Bảng biến thiên của hàm số:

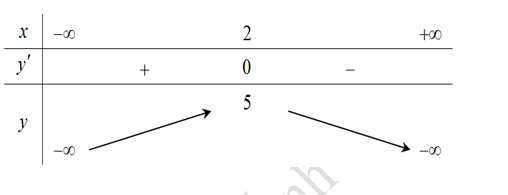
Dựa vào bảng biến thiên suy ra khẳng định D sai.

Câu 4:         Hàm số \[y = {x^2} - 4x + 11\] đồng biến trên khoảng nào trong các khoảng sau đây?

A. \[( - 2; + \infty )\]          B. \[( - \infty ; + \infty )\] C. \[(2; + \infty )\]           D. \[( - \infty ;2)\]

Lời giải

Chọn C

Ta có bảng biến thiên:

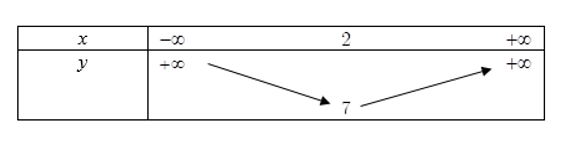
Từ bảng biến thiên ta thấy, hàm số đồng biến trên khoảng1010011011.5606 </w:wordDocument"> <![endif]-->\[(2; + \infty )\]

Câu 5:         Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\)là

A. \(\left( { - \infty ; - 2} \right)\).                             B. \(\left( { - \infty ;2} \right)\).                                        C. \(\left( { - 2; + \infty } \right)\).                         D. \(\left( {2; + \infty } \right)\).

Lời giải

Chọn D

Hàm số \(y = {x^2} - 4x + 3\)có \(a = 1 > 0\) nên đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\).

Vì vậy hàm số đồng biến trên \(\left( {2; + \infty } \right)\).

Câu 6:         Khoảng nghịch biến của hàm số \(y = {x^2} - 4x + 3\)là

A. \(\left( { - \infty ; - 4} \right)\).                            B. \(\left( { - \infty ; - 4} \right)\).                                        C. \(\left( { - \infty ;2} \right)\).                             D. \(\left( { - 2; + \infty } \right)\).

Lời giải

Chọn C

Hàm số \(y = {x^2} - 4x + 3\)có hệ số \(a = 1 > 0\) nên đồng biến trên khoảng \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\).

Vì vậy hàm số đồng biến trên \(\left( { - \infty ;2} \right)\).

Câu 7:         Cho hàm số \(y =  - {x^2} + 4x + 3.\) Chọn khẳng định đúng.

A. Hàm số đồng biến trên \(\mathbb{R}.\)            B. Hàm số nghịch biến trên \(\mathbb{R}.\)

C. Hàm số đồng biến trên \(\left( {2; + \infty } \right)\).                               D. Hàm số nghịch biến trên \(\left( {2; + \infty } \right)\).

Lời giải

Chọn D

Do \(a =  - 1\) nên hàm số đồng biến trên \[\left( { - \infty ;2} \right)\] nghịch biến trên \(\left( {2; + \infty } \right)\).

Câu 8:         Hàm số \(f\left( x \right) = {x^2} - 2x + 3\) đồng biến trên khoảng nào dưới đây?

A. \(\left( {1; + \infty } \right)\).                               B. \(\left( { - 2; + \infty } \right)\).                            C. \(\left( { - \infty ;1} \right)\).                             D. \(\left( {\frac{1}{2}; + \infty } \right)\).

Lời giải

Chọn A

Ta có hàm số \(\left( P \right):\,y = f\left( x \right) = {x^2} - 2x + 3\) là hàm số bậc hai có hệ số \(a = 1\);nên \[\left( P \right)\] có bề lõm hướng lên.

Hoành độ đỉnh của parabol \({x_I} = \frac{{ - b}}{{2a}} = 1\). Do đó hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).

Câu 9:         Hàm số \(y = 2{x^2} - 4x + 1\) đồng biến trên khoảng nào?

A. \(\left( { - \infty ; - 1} \right)\).                             B. \(\left( { - \infty ;1} \right)\).                                        C. \(\left( { - 1; + \infty } \right)\).                         D. \(\left( {1; + \infty } \right)\).

Lời giải

Chọn D

Hàm số bậc hai có \(a = 2 > 0;\, - \frac{b}{{2a}} = 1\) nên hàm số đồng biến trên \(\left( {1; + \infty } \right)\).

Câu 10:      Hàm số \[y =  - 3{x^2} + x - 2\] nghịch biến trên khoảng nào sau đây?

A. \(\left( {\frac{1}{6}; + \infty } \right).\)                B. \(\left( { - \infty ; - \frac{1}{6}} \right).\)                            C. \(\left( { - \frac{1}{6}; + \infty } \right).\)           D. \(\left( { - \infty ;\frac{1}{6}} \right).\)

Lời giải

Chọn A

\[\left( P \right):y = f\left( x \right) =  - 3{x^2} + x - 2\], TXĐ: \[D = \mathbb{R}\].

Có \[a =  - 3\], đỉnh \[S\] có hoành độ \[x = \frac{1}{6}\].

Nên hàm số \[y = f\left( x \right)\] nghịch biến trong khoảng \(\left( {\frac{1}{6}; + \infty } \right).\)

Câu 11:      Cho hàm số \(y =  - {x^2} + 6x - 1\). Hàm số đồng biến trên khoảng nào dưới đây?

A. \(\left( { - \infty ;3} \right)\)                                 B. \(\left( {3; + \infty } \right)\)                                        C. \(\left( { - \infty ;6} \right)\)                              D. \(\left( {6; + \infty } \right)\)

Lời giải

Ta có \(a =  - 1 < 0,\frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.\left( { - 1} \right)}} = 3\). Suy ra hàm số đồng biến trên khoảng \(\left( { - \infty ;3} \right)\).

Đáp án       A.

Câu 12:      Cho hàm số\[y = {x^2} - 3mx + {m^2} + 1\] \[\left( 1 \right)\], \[m\] là tham số. Khi \[m = 1\] hàm số đồng biến trên khoảng nào?

A. \[\left( { - \infty ;\frac{3}{2}} \right)\].                  B. \[\left( {\frac{1}{4}; + \infty } \right)\].                            C. \[\left( { - \infty ;\frac{1}{4}} \right)\].                D. \[\left( {\frac{3}{2}; + \infty } \right)\].

Lời giải

Chọn D

Khi \[m = 1\], hàm số trở thành \[y = {x^2} - 3x + 2\]

Tập xác định: \[D = \mathbb{R}\].

Đỉnh \[I\left( {\frac{3}{2}; - \frac{1}{4}} \right)\].

Bảng biến thiên:

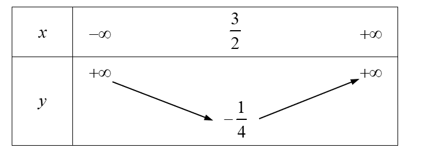
Hàm số đồng biến trên \[\left( {\frac{3}{2}; + \infty } \right)\].

Câu 13:      Có bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = {x^2} - 2\left( {m + 1} \right)x - 3\) đồng biến trên khoảng \(\left( {4;2018} \right)\)?

A. 0                                  B. 1                               C. 2                               D. 3

Lời giải

Hàm số có \(a = 1 > 0,\frac{{ - b}}{{2a}} = m + 1\) nên đồng biến trên khoảng \(\left( {m + 1; + \infty } \right)\).

Do đó để hàm số đồng biến trên khoảng \(\left( {4;2018} \right)\) thì ta phải có

\(\left( {4;2018} \right) \subset \left( {m + 1; + \infty } \right) \Leftrightarrow m + 1 \le 4 \Leftrightarrow m \le 3\).

Vậy có ba giá trị nguyên dương của m thỏa mãn yêu cầu bài toán là 1, 2, 3.

Đáp án       D.

Câu 14:      Tìm tất cả các giá trị của \(b\) để hàm số \(y = {x^2} + 2(b + 6)x + 4\) đồng biến trên khoảng \(\left( {6; + \infty } \right)\).

A. \(b \ge 0\).                   B. \(b =  - 12\).              C. \(b \ge  - 12\).           D. \(b \ge  - 9\).

Lời giải

Chọn C

Hàm số \(y = f(x) = {x^2} + 2(b + 6)x + 4\) là hàm số bậc hai có hệ sô \(a = 1 > 0\), \( - \frac{b}{{2a}} =  - b - 6\)nên có bảng biến thiên

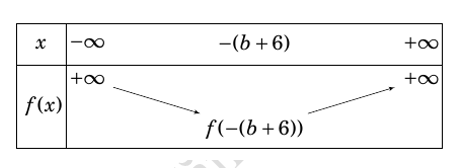
Từ bảng biến thiên ta có:

Hàm số đồng biến trên \(\left( {6; + \infty } \right)\)thì \( \Leftrightarrow \left( {6; + \infty } \right) \subset \left( { - b - 6; + \infty } \right) \Leftrightarrow  - b - 6 \le 6 \Leftrightarrow b \ge  - 12.\).

Câu 15:      Hàm số \[y =  - {x^2} + 2\left( {m - 1} \right)x + 3\]nghịch biến trên \[\left( {1; + \infty } \right)\] khi giá trị m thỏa mãn:

A. \[m \le 0\].                    B. \[m > 0\].                   C. \[m \le 2\].                 D. \[0 < m \le 2\]

Lời giảiss

Chọn C

Đồ thị hàm số có trục đối xứng là đường \[x = m - 1\]. Đồ thị hàm số đã cho có hệ số \[{x^2}\] âm nên sẽ đồng biến trên \[\left( { - \infty ;m - 1} \right)\] và nghịch biến trên \[\left( {m - 1; + \infty } \right)\]. Theo đề, cần: \[m - 1 \le 1 \Leftrightarrow m \le 2\].

Câu 16:      Tìm tất cả các giá trị của tham số \(m\) để hàm số \[y =  - {x^2} + 2\left| {m + 1} \right|x - 3\] nghịch biến trên\[\left( {2; + \infty } \right).\]

A. \[\left[ {\begin{array}{*{20}{c}}{m \le  - 3}\\{m \ge 1}\end{array}} \right.\;\].                                        B. \[ - 3 < m < 1\].         C. \[ - 3 \le m \le 1\].      D. \[\left[ {\begin{array}{*{20}{c}}{m <  - 3}\\{m > 1}\end{array}} \right.\;\].

Lời giải

Chọn C

Hàm số \[y =  - {x^2} + 2\left| {m + 1} \right|x - 3\] có \(a =  - 1 < 0;\, - \frac{b}{{2a}} = \left| {m + 1} \right|\) nên hàm số nghịch biến trên \(\left( {\left| {m + 1} \right|; + \infty } \right)\).

Để hàm số nghịch biến trên \(\left( {2; + \infty } \right)\) thì \(\left( {2; + \infty } \right) \subset \left( {\left| {m + 1} \right|; + \infty } \right)\)

\( \Leftrightarrow \left| {m + 1} \right| \le 2 \Leftrightarrow  - 2 \le m + 1 \le 2 \Leftrightarrow  - 3 \le m \le 1\).

Câu 17:      Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để hàm số \(y = {x^2} + (m - 1)x + 2m - 1\) đồng biến trên khoảng \(\left( { - 2; + \infty } \right)\). Khi đó tập hợp \(\left( { - 10;10} \right) \cap S\) là tập nào?

A. \(\left( { - 10;5} \right)\).                                    B. \(\left[ {5;10} \right)\).                                        C. \(\left( {5;10} \right)\).                                     D. \(\left( { - 10;5} \right]\).

Lời giải

Chọn B

Gọi \[\left( P \right)\] là đồ thị của \(y = f\left( x \right) = {x^2} + (m - 1)x + 2m - 1\).

\[y = f\left( x \right)\]là hàm số bậc hai có hệ số \(a = 1\).

Gọi \[I\] là đỉnh của \[\left( P \right)\], có \[{x_I} = \frac{{1 - m}}{2}\].

Nên hàm số đồng biến trên khoảng \(\left( {\frac{{1 - m}}{2}; + \infty } \right)\).

Do đó để hàm số trên khoảng \(\left( { - 2; + \infty } \right)\) khi \(\frac{{1 - m}}{2} \le  - 2\) \( \Leftrightarrow m \ge 5\).

Suy ra tập \(S = \left[ {5; + \infty } \right)\). Khi đó \(\left( { - 10;10} \right) \cap S = \left[ {5;10} \right)\).

Câu 18:      Tìm tất cả các giá trị dương của tham số \(m\) để hàm số \(f\left( x \right) = m{x^2} - 4x - {m^2}\) luôn nghịch biến trên \(\left( { - 1;2} \right)\).

A. \(m \le 1\).                   B. \( - 2 \le m \le 1\).     C. \(0 < m \le 1\).           D. \(0 < m < 1\).

Lời giải

Chọn C

- Với \(m > 0\), ta có hàm số \(f\left( x \right) = m{x^2} - 4x - {m^2}\) nghịch biến trên \(\left( { - \infty ;\frac{2}{m}} \right)\), suy ra hàm nghịch biến trên \(\left( { - 1;2} \right)\) khi \(\left( { - 1;2} \right) \subset \left( { - \infty ;\frac{2}{m}} \right) \Leftrightarrow 2 \le \frac{2}{m} \Leftrightarrow 0 < m \le 1\).

Câu 19:      Cho hàm số \(y = {x^2} - 2mx + {m^2}\,\,\left( P \right)\). Khi \(m\)thay đổi, đỉnh của Parabol \(\left( P \right)\)luôn nằm trên đường nào sau đây?

A. \(y = 0\).                      B. \(x = 0\).                                C. \(y = x\).                    D. \(y = {x^2}\).

Lời giải

Chọn A

Tọa độ đỉnh \(I\)của Parabol là \(I\left( {m\,;\,0} \right)\), nên \(I\)luôn thuộc đường thẳng \(y = 0\).

Câu 20:      Cho hàm số \(y = {x^2} - 4mx + 4{m^2}\,\,\left( P \right)\). Khi \(m\)thay đổi, đỉnh của Parabol \(\left( P \right)\)luôn nằm trên đường nào sau đây?

A. \(x = 0\).                      B. \(y = 0\).                                C. \(y = 2{x^2}\).            D. \(y = {x^2}\).

Lời giải

Chọn B

Tọa độ đỉnh \(I\)của Parabol là \(I\left( {2m\,;\,0} \right)\), nên \(I\)luôn nằm trên đường thẳng \(x = 0\).

Câu 21:      Tìm giá trị của tham số \(m\)để đỉnh \(I\)của đồ thị hàm số \(y =  - {x^2} + 6x + m\) thuộc đường thẳng \(y = x + 2019\).

A. \(m = 2020\).               B. \(m = 2000\).            C. \(m = 2036\).            D. \(m = 2013\).

Lời giải

Chọn D

Đồ thị hàm số \(y =  - {x^2} + 6x + m\)là parabol có đỉnh \(I\left( {3;9 + m} \right)\).

Đỉnh \(I\left( {3;9 + m} \right)\)thuộc đường thẳng \(y = x + 2019 \Leftrightarrow 9 + m = 3 + 2019 \Leftrightarrow m = 2013\).