Tài liệu chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn Toán lớp 10 sách Chân trời sáng tạo gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Chân trời sáng tạo word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Tài liệu gồm 4 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Hệ bất phương trình bậc nhất hai  :

Chuyên đề 2: HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Tương tự hệ bất phương trình một ẩn

Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn \[x,\,\,y\] mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.

Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.

II. BIỂU DIỄN TẬP NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất 2 ẩn ta làm nư sau:

- Trong cùng hệ toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.

- Phần không bị gạch là miền nghiệm cần tìm.

III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN

Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính.

DẠNG 1: CÁC BÀI TOÁN LIÊN BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Câu 1:         Biểu diễn hình học tập nghiệm của bất phương trình \[2x + y \le 3\].

Lời giải

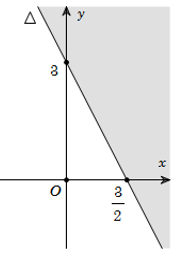
Vẽ đường thẳng \[\Delta :2x + y = 3.\]

Lấy gốc tọa độ \[O\left( {0;0} \right),\] ta thấy \[O \notin \Delta \] và có \[2.0 + 0 < 3\] nên nửa mặt phẳng bờ \[\Delta \] chứa gốc tọa độ \[O\] là miền nghiệm của bất phương trình đã cho (miền không bị tô đậm trong hình).

Câu 2:         Biểu diễn hình học tập nghiệm của bất phương trình \[ - 3x + y + 2 \le 0\].

Lời giải

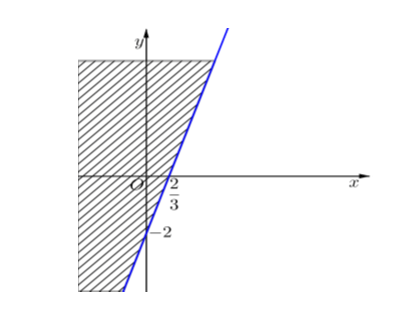
Trước hết, ta vẽ đường thẳng \(\left( d \right): - 3x + y + 2 = 0.\)

Ta thấy \(\left( {0\,\,;\,\,0} \right)\) không là nghiệm của bất phương trình.

Vậy miền nghiệm là nửa mặt phẳng bờ \(\left( d \right)\) không chứa điểm \(\left( {0\,\,;\,\,0} \right).\)

Câu 3:         Biểu diễn hình học tập nghiệm của bất phương trình \[x + 3 + 2(2y + 5) < 2(1 - x)\].

Lời giải

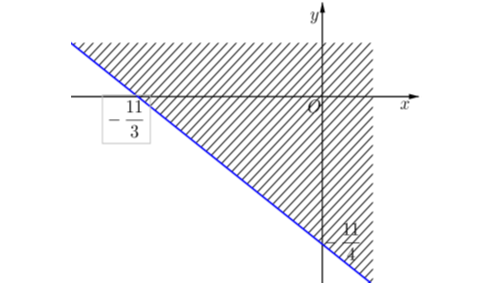
Đầu tiên, thu gọn bất phương trình đề bài đã cho về thành \(3x + 4y + 11 < 0.\)

Ta vẽ đường thẳng \(\left( d \right):3x + 4y + 11 = 0.\)

Ta thấy \(\left( {0\,\,;\,\,0} \right)\) không là nghiệm của bất phương trình.

Vậy miền nghiệm là nửa mặt phẳng (không kể bờ \(\left( d \right)\)) không chứa điểm \(\left( {0\,\,;\,\,0} \right).\)

Câu 4:         Biểu diễn hình học tập nghiệm của bất phương trình \[\left( {1 + \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y \ge 2\].

Lời giải

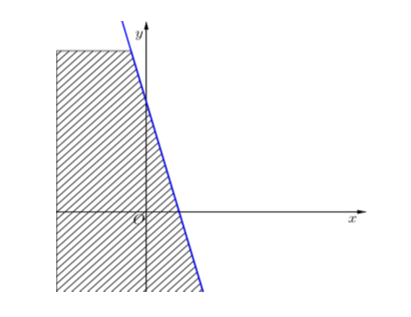
Trước hết, ta vẽ đường thẳng \(\left( d \right):\left( {1 + \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y = 2.\)

Ta thấy \(\left( {0\,\,;\,\,0} \right)\) không là nghiệm của bất phương trình đã cho.

Vậy miền nghiệm là nửa mặt phẳng bờ \(\left( d \right)\) không chứa điểm \(\left( {0\,\,;\,\,0} \right).\)

DẠNG 2: CÁC BÀI TOÁN LIÊN HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Câu 1:         Biểu diễn hình học tập nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}3x + y \le 6\\x + y \le 4\\x \ge 0\\y \ge 0\end{array} \right..\]

Lời giải

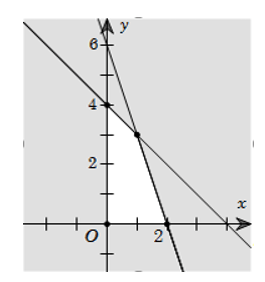
Vẽ các đường thẳng

\[\begin{array}{l}{d_1}:3x + y = 6\\{d_2}:x + y = 4\\{d_2}:x = 0\,\,\,\,\,\,\left( {Oy} \right)\\{d_2}:y = 0\,\,\,\,\,\,\left( {Ox} \right)\end{array}\]

Vì điểm \[{M_0}\left( {1;1} \right)\] có tọa độ thỏa mãn tất cả các bất phương trình trong hệ trên nên ta tô đậm các nửa mặt phẳng bờ \[\left( {{d_1}} \right),\] \[\left( {{d_2}} \right),\] \[\left( {{d_3}} \right),\] \[\left( {{d_4}} \right)\] không chứa điểm \[{M_0}.\] Miền không bị tô đậm (hình tứ giác \[OCIA\] kể cả bốn cạnh \[AI,\,\,IC,\,\,CO,\,\,OA\]) trong hình vẽ là miền nghiệm của hệ đã cho.

Câu 2:         Tìm miền nghiệm của hệ bất phương trình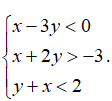 

Lời giải

Trước hết, ta vẽ ba đường thẳng:

\(\left( {{d_1}} \right):x - 3y = 0\)

\(\left( {{d_3}} \right):x + y = 2\)

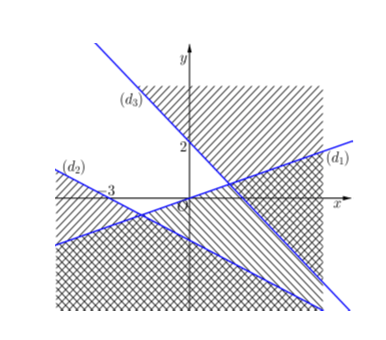
Ta thấy \(\left( { - 1\,\,;\,\,0} \right)\) là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm \(\left( { - 1\,\,;\,\,0} \right)\) thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ miền không thích hợp, miền không bị gạch là miền nghiệm của hệ.

Câu 3:         Tìm trị lớn nhất của biểu thức \[F\left( {x;y} \right) = x + 2y\], với điều kiện \(\left\{ {\begin{array}{*{20}{c}}{0 \le y \le 4}\\{x \ge 0}\\{x - y - 1 \le 0}\\{x + 2y - 10 \le 0}\end{array}} \right.\).

Lời giải

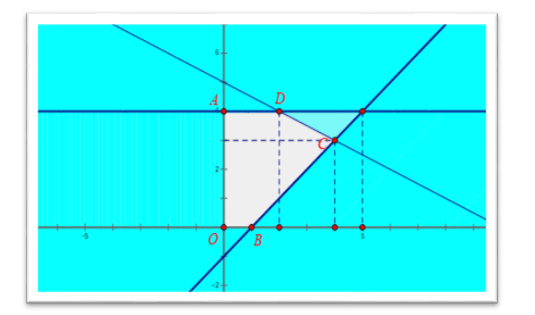
Vẽ đường thẳng \({d_1}:x - y - 1 = 0\), đường thẳng \({d_1}\) qua hai điểm \(\left( {0;\, - 1} \right)\) và \(\left( {1;\,0} \right)\).

Vẽ đường thẳng \({d_2}:x + 2y - 10 = 0\), đường thẳng \({d_2}\) qua hai điểm \(\left( {0;\,5} \right)\) và \(\left( {2;\,4} \right)\).

Vẽ đường thẳng \({d_3}:y = 4\).

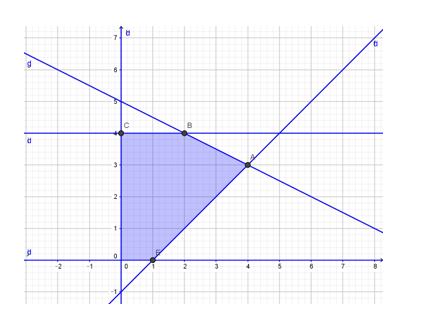
Miền nghiệm là ngũ giác \(ABCOE\) với \(A\left( {4;\,3} \right),\,B\left( {2;\,4} \right),\,C\left( {0;\,4} \right),\,E\left( {1;\,0} \right)\).

Ta có: \[F\left( {4;3} \right) = 10\], \[F\left( {2;4} \right) = 10\], \[F\left( {0;4} \right) = 8\], \[F\left( {1;0} \right) = 1\], \[F\left( {0;0} \right) = 0\].

Vậy giá trị lớn nhất của biết thức \[F\left( {x;y} \right) = x + 2y\] bằng \(10\).