Tài liệu chuyên đề Mệnh đề và tập hợp Toán lớp 10 sách Chân trời sáng tạo gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Chân trời sáng tạo word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Mệnh đề và tập hợp

Tài liệu gồm 4 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Tập hợp :

Chuyên đề 2: TẬP HỢP

I. Lý thuyết

1. Nhắc lại về tập hợp

Như đã biết ở cấp Trung học cơ sở, trong toán học, người ta dùng từ tập hợp để chỉ một nhóm đối tượng nào đó hoàn toàn xác định. Mỗi đối tượng trong nhóm gọi là một phần tử của tập hợp đó.

Tập hợp (còn gọi là tập) là một khái niệm cơ bản của toán học, không định nghĩa.

Giả sử đã cho tập hợp \[A.\]

\( \bullet \) Để chỉ \[a\] là một phần tử của tập hợp \[A,\] ta viết \[a \in A\] (đọc là \[a\] thuộc \[A\]).

\( \bullet \) Để chỉ \[a\] không phải là một phần tử của tập hợp \[A,\] ta viết \[a \notin A\] (đọc là \[P\] không thuộc \[A\]).

Cách xác định tập hợp

Một tập hợp có thể được xác định bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó.

Vậy ta có thể xác định một tập hợp bằng một trong hai cách sau

\( \bullet \) Liệt kê các phần tử của nó.

\( \bullet \) Chỉ ra tính chất đặc trưng cho các phần tử của nó.

Người ta thường minh họa tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven.

Tập hợp rỗng

Tập hợp rỗng, kí hiệu là \[\emptyset ,\] là tập hợp không chứa phần tử nào.

Nếu \[A\] không phải là tập hợp rỗng thì \[A\] chứa ít nhất một phần tử.

\[A \ne \emptyset  \Leftrightarrow \exists x:\,\,x \in A.\]

2. Tập con và hai tập hợp bằng nhau

Cho hai tập hợp A và B. Nếu mọi phần tử của A đều là phần tử của B thì ta nói tập hợp A là tập con của tập hợp B và kí hiệu A ⊂ B (đọc là A chứa trong B), hoặc B ⊃ A (đọc là B chứa A).

Nhận xét:

- A ⊂ A và ∅ ⊂ A với mọi tập hợp A.

- Nếu A không phải là tập con của B thì ta kí hiệu A ⊄ B (đọc là A không chứa trong B hoặc B không chứa A).

- Nếu A ⊂ B hoặc B ⊂ A thì ta nói A và B có quan hệ bao hàm.

Như vậy \[A \subset B \Leftrightarrow \left( {\forall x:\,\,x \in A \Rightarrow x \in B} \right).\]

Nếu \[A\] không phải là một tập con của \[B,\] ta viết \[A \not\subset B.\]

Trong toán học, người ta thường minh hoạ tập hợp bằng một hình phẳng được bao quanh bởi một đường cong kín, gọi là biểu đồ Ven (đặt theo tên nhà toán học, nhà triết học người Anh John Venn). Theo cách này, ta có thể minh hoạ A là tập con của B như Hình 1.

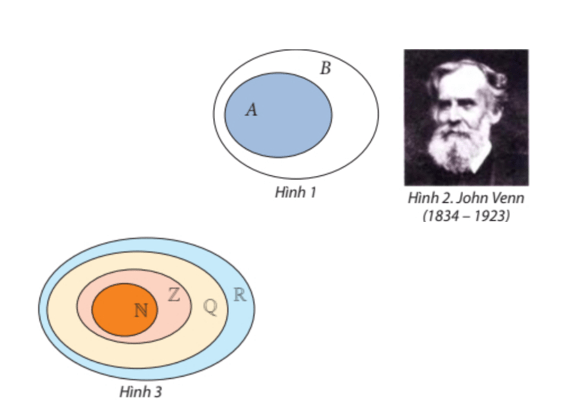
Chú ý:

Giữa các tập hợp số quen thuộc (tập số tự nhiên, tập số nguyên, tập số hữu ti, tập số thực), ta có quan hệ bao hàm:

N ⊂ Z ⊂ Q ⊂ R.

Hai tập hợp \[A\] và \[B\]gọi là bằng nhau, kí hiệu \[A = B.\], nếu \[A \subset B\] và \[B \subset A\].

\[A = B \Leftrightarrow \left( {\forall x:\,\,x \in A \Leftrightarrow x \in B} \right).\]

Nói cách khác, hai tập hợp A và B bằng nhau nếu mỗi phần tử của tập hợp này cũng là phần tử của tập hợp kia và ngược lại.

3. Một số tập con của tập hợp số thực

Sau này ta thường sử dụng các tập con của tập số thực sau đây (\(a\) và \(b\) là các số thực,\(a < b\)):

Tên gọi và kí hiệu	Tập hợp	Biểu diễn trên trục số
Tập số thực \(\left( { - \infty ; + \infty } \right)\)	\(\mathbb{R}\)
Đoạn \(\left[ {a;b} \right]\)	\[\left[ {a;b} \right] = \left\{ {x \in \mathbb{R}|a \le x \le b} \right\}.\]
Khoảng \(\left( {a;b} \right)\)	\[\left( {a;b} \right)\, = \left\{ {x \in \mathbb{R}|a < x < b} \right\}\]
Nửa khoảng \(\left[ {a;b} \right)\)	\[\left[ {a;b} \right)\,\, = \left\{ {x \in \mathbb{R}|a \le x < b} \right\}\]
Nửa khoảng (a;b]	\[\left( {a;b} \right]\,\, = \left\{ {x \in \mathbb{R}|a < x \le b} \right\}\]
Nửa khoảng \[\left( { - \,\infty ;a} \right]\]	\[\left( { - \,\infty ;a} \right] = \left\{ {x \in \mathbb{R}|x \le a} \right\}.\]
Nửa khoảng \[\left[ {a; + \,\infty } \right)\]	\[\left[ {a; + \,\infty } \right) = \left\{ {x \in \mathbb{R}|a \le x} \right\}\]
Khoảng \[\left( {a; + \,\infty } \right)\]	\[\left( {a; + \,\infty } \right) = \left\{ {x \in \mathbb{R}|a < x} \right\}\]
Khoảng \[\left( { - \,\infty ;a} \right)\]	\[\left( { - \,\infty ;a} \right) = \left\{ {x \in \mathbb{R}|x < a} \right\}\]

Trong các ký hiệu trên, kí hiệu \( - \infty \) đọc là âm vô cực, kí hiệu \( + \infty \) đọc là dương vô cực.

 DẠNG 1: XÁC ĐỊNH MỘT TẬP HỢP

PHƯƠNG PHÁP

Để xác định một tập hợp, ta có 2 cách sau:

w Liệt kê các phần tử của tập hợp.

w Chỉ ra tính chất đặc trưng của tập hợp.

Bài 1. Viết lại tập hợp \(A = \left\{ {x \in \mathbb{R}\left| {\left( {2{x^2} - 5x + 3} \right)\left( {{x^2} - 4x + 3} \right) = 0} \right.} \right\}\) bằng cách liệt kê các phần tử của nó.

Lời giải

Ta có \(\left( {2{x^2} - 5x + 3} \right)\left( {{x^2} - 4x + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2{x^2} - 5x + 3 = 0\\{x^2} - 4x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{3}{2}\\x = 1\\x = 3\end{array} \right.\).

Vì \(x \in \mathbb{R}\) nên \(A = \left\{ {1;\frac{3}{2};3} \right\}\).

Bài 2. Viết lại tập hợp \(A = \left\{ {x \in \mathbb{N}\left| {\left( {2{x^2} - 5x + 3} \right)\left( {{x^2} - 4x + 3} \right) = 0} \right.} \right\}\) bằng cách liệt kê các phần tử của nó.

Lời giải

Ta có \(\left( {2{x^2} - 5x + 3} \right)\left( {{x^2} - 4x + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2{x^2} - 5x + 3 = 0\\{x^2} - 4x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{3}{2}\\x = 1\\x = 3\end{array} \right.\).

Vì \(x \in \mathbb{N}\) nên \(A = \left\{ {1;3} \right\}\).

Bài 3. Viết lại tập hợp \(A = \left\{ {x \in \mathbb{N}\left| {x < 5} \right.} \right\}\) bằng cách liệt kê các phần tử của nó.

Lời giải

Ta có \(x < 5\)và \(x \in \mathbb{N}\)nên \(x \in \left\{ {0;1;2;3;4} \right\}\)

Vậy \(A = \left\{ {0;1;2;3;4} \right\}\)

Bài 4. Viết mỗi tập hợp \(A = \left\{ {0;{\rm{ 1}};{\rm{ 2}};{\rm{ 3}};{\rm{ 4}}} \right\}\) bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó.

Lời giải

Ta nhận thấy các phần tử của tập hợp \(A\) là các số tự nhiên và nhỏ hơn 5. Do đó \(A = \left\{ {x \in \mathbb{N}\left| {x < 5} \right.} \right\}\).

Bài 5. Viết mỗi tập hợp \(A = \left\{ {{\rm{9}};{\rm{ 36}};{\rm{ 81}};{\rm{ 144}}} \right\}\) bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó.

Lời giải

Ta có \(9 = {3^2}\), \(36 = {6^2}\), \(81 = {9^2}\), \(144 = {12^2}\) và các số \(3,6,9,12\) đều là bội của 3. Do đó ta viết lại tập hợp \(A\)bằng cách chỉ ra tính chất đặc trưng là \(A = \left\{ {\left. {{{\left( {3k} \right)}^2}} \right|k \in {\mathbb{N}^*},k \le 4} \right\}\).

Bài 6. Liệt kê tất cả các phần tử của tập hợp \(A\) gồm các số tự nhiên chia hết cho 3 và nhỏ hơn 25.

Lời giải

       Ta có \(A = \left\{ {0\,;3\,;6\,;9\,;12\,;15\,;18\,;21\,;23} \right\}\).

Bài 7. Liệt kê các phần tử của tập hợp \[X = \left\{ {x \in \mathbb{R}\left| {\,2{x^2} - 5x + 3 = 0} \right.} \right\}\].

Lời giải

Ta có \[2{x^2} - 5x + 3 = 0\]\[ \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \mathbb{R}\\x = \frac{3}{2} \in \mathbb{R}\end{array} \right.\]\[ \Rightarrow X = \left\{ {1\,;\,\frac{3}{2}} \right\}\].

 Bài 8. Viết tập hợp \(B = \left\{ {x \in \mathbb{N}\left| {\,\left( {9 - {x^2}} \right)\left( {{x^2} - 3x + 2} \right) = 0} \right.} \right\}\)dưới dạng liệt kê các phần tử.

Lời giải

Ta có \(\left( {9 - {x^2}} \right)\left( {{x^2} - 3x + 2} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}9 - {x^2} = 0\\{x^2} - 3x + 2 = 0\end{array} \right.\) 

Vậy \(B = \left\{ {3\,;1\,;2} \right\}\).

Bài 9. Viết tập hợp \(A = \left\{ {x \in \mathbb{Q}\left| {\,\left( {5 - {x^2}} \right)\left( {{x^2} - 5x + 6} \right) = 0} \right.} \right\}\)dưới dạng liệt kê các phần tử.

Lời giải

Ta có \(\left( {5 - {x^2}} \right)\left( {{x^2} - 5x + 6} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}5 - {x^2} = 0\\{x^2} - 5x + 6 = 0\end{array} \right.\) 

Vậy \(A = \left\{ {2\,;3} \right\}\).

Bài 10. Tính tổng tất cả các phần tử của tập hợp \(A = \left\{ {x \in \mathbb{N}\left| {\,\frac{3}{{x - 2}} \in \mathbb{Z}} \right.} \right\}\).

Lời giải

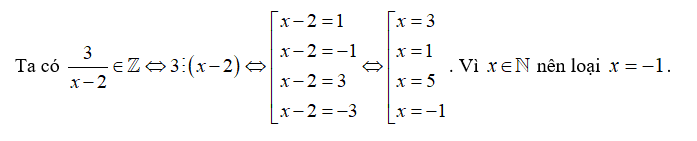
Suy ra \(A = \left\{ {1\,;3\,;5} \right\}\). Vậy tổng tất cả các phần tử của tập hợp \(A\) là \(1 + 3 + 5 = 9\).

Bài 11.         Lớp 10A có \(10\) học sinh giỏi Toán, \(10\) học sinh giỏi Lý, \(11\) học sinh giỏi hóa, \(6\)học sinh giỏi cả Toán và Lý, \(5\) học sinh giỏi cả Hóa và Lý, \(4\) học sinh giỏi cả Toán và Hóa, \(3\) học sinh giỏi cả ba môn Toán, Lý, Hóa. Tính học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A?

Lời giải

Theo giả thiết đề bài cho, ta có biểu đồ Ven:

Dựa vào biểu đồ Ven, ta có học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là

Số học sinh giỏi Toán: \(6 + 4 + 3 = 13\).

Số học sinh giỏi Lý: \(6 + 5 + 3 = 14\).

Số học sinh giỏi Hóa: \(4 + 5 + 3 = 12\).

Ta lại có:

Số học sinh giỏi cả Toán và Lý: \(6\).

Số học sinh giỏi cả Toán và Hóa: \(4\).

Số học sinh giỏi cả Hóa và Lý: \(5\).

Và số học sinh giỏi cả Toán, Lý và Hóa là \(3\).

Số học sinh giỏi hơn một môn là \(4 + 6 + 5 + 3 = 18\).

Bài 12.         Cho \(A = \left( {2; + \infty } \right)\), \(B = \left( {m; + \infty } \right)\). Tìm điều kiện cần và đủ của \(m\) để \(B\) là tập con của \(A\)?

Lời giải

Ta có: \(B \subset A\) khi và chỉ khi \(\forall x \in B \Rightarrow x \in A\)\( \Rightarrow m \ge 2\).

Bài 13.         Xác định số phần tử của tập hợp \(X = \left\{ {n \in \mathbb{N}|n\, \vdots \,4\,,\,n < 2017} \right\}\).

Lời giải

Tập hợp \(X\) gồm các phần tử là những số tự nhiên nhỏ hơn \(2017\) và chia hết cho \(4\).

Từ \(0\) đến \(2015\) có \(2016\) số tự nhiên, ta thấy cứ \(4\) số tự nhiên liên tiếp sẽ có duy nhất một số chia hết cho \(4\). Suy ra có \(504\) số tự nhiên chia hết cho \(4\) từ \(0\) đến \(2015\). Hiển nhiên \(2016\, \vdots \,4\).

Vậy có tất cả \(505\) số tự nhiên nhỏ hơn \(2017\) và chia hết cho \(4\).