Với lời giải Toán 11 trang 28 Tập 2 chi tiết trong Bài 22: Hai đường thẳng vuông góc sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 Bài 22: Hai đường thẳng vuông góc

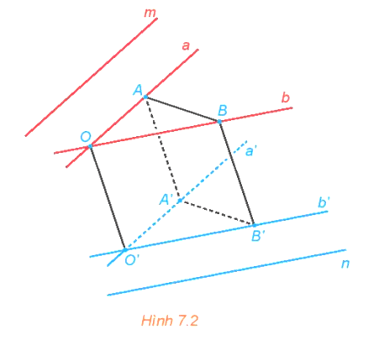
HĐ1 trang 28 Toán 11 Tập 2: Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O, O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a', b' tương ứng song song với m, n (H.7.2).

a) Mỗi cặp đường thẳng a, a' và b, b' có cùng thuộc một mặt phẳng hay không?

b) Lấy các điểm  A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A', đường thẳng qua B song song với OO' cắt b' tại B'. Giải thích vì sao OAA'O'; OBB'O'; ABB'A' là các hình bình hành.

c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'.

(Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B' ).

Lời giải:

a) Mỗi cặp đường thẳng a, a' và b, b' cùng thuộc một mặt phẳng vì a // a' và b // b'.

b) Có a // a' nên OA // O'A'.

Vì OA // O'A' và AA' // OO' nên OAA'O' là hình bình hành.

Có b // b' nên OB // O'B'.

Vì OB // O'B' và BB' // OO' nên OBB'O' là hình bình hành.

Vì OAA'O' là hình bình hành nên AA' = OO', OBB'O' là hình bình hành nên BB' = OO', suy ra AA' = BB'.

Vì AA' // OO' và BB' // OO' nên BB' // AA'.

Vì  AA' = BB' và BB' // AA' nên ABB'A' là hình bình hành.

c) Ta có góc giữa hai đường thẳng a, b là $\widehat{AOB}$ và góc giữa hai đường thẳng a', b' là $\widehat{\mathrm{A\text{'}}\mathrm{O\text{'}}\mathrm{B\text{'}}}$.

Vì OAA'O' là hình bình hành nên OA = O'A'.

Vì OBB'O' là hình bình hành nên OB = O'B'.

Vì ABB'A' là hình bình hành nên AB = A'B'.

Do đó DOAB và DO'A'B' có các cạnh tương ứng bằng nhau.

Áp dụng định lí côsin cho DOAB có: $cos\widehat{AOB}=\frac{O{A}^2+O{B}^2-A{B}^2}{2\cdot OA\cdot OB}$.

Áp dụng định lí côsin cho DO'A'B' có: $cos\widehat{A^{\text{'}}{O}^{\text{'}}{B}^{\text{'}}}=\frac{O^{\text{'}}{A^{\text{'}}}^2+O^{\text{'}}{B^{\text{'}}}^2-A^{\text{'}}{B^{\text{'}}}^2}{2\cdot O^{\text{'}}{A}^{\text{'}}\cdot O^{\text{'}}{B}^{\text{'}}}$.

Do DOAB và DO'A'B' có các cạnh tương ứng bằng nhau nên $cos\widehat{AOB}=cos\widehat{A^{\text{'}}{O}^{\text{'}}{B}^{\text{'}}}$.

Vậy góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b' bằng nhau.

Câu hỏi trang 28 Toán 11 Tập 2: Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) và (a', b') có mối quan hệ gì?

Lời giải:

Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) = (a', b').