Với tóm tắt lý thuyết Toán lớp 8 Bài 2: Tọa độ của một điểm và đồ thị của hàm số sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 8.
Lý thuyết Toán lớp 8 Bài 2: Tọa độ của một điểm và đồ thị của hàm số
A. Lý thuyết Tọa độ của một điểm và đồ thị của hàm số
1. Tọa độ của một điểm
a. Khái niệm:
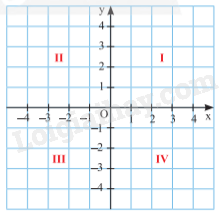
Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.
Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: góc phần tư thứ I, II, III, IV.
b. Tọa độ của một điểm:
Trong mặt phẳng tọa độ, mỗi điểm P xác định duy nhất một cặp số (a; b) và mỗi cặp số (a; b) xác định duy nhất một điểm M.
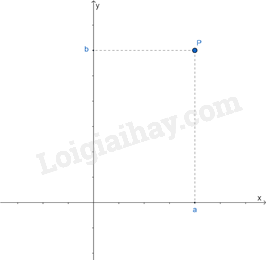
Cặp số (a; b) gọi là tọa độ của M, kí hiệu là M(a; b), trong đó a là hoành độ, b là tung độ của điểm M.
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.
2. Xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó
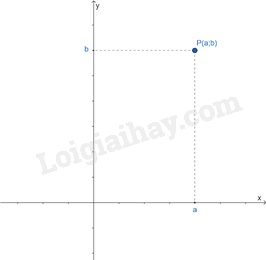
Để xác định một điểm điểm P có tọa độ là (a; b), ta thực hiện các bước sau:
- Tìm trên trục hoành điểm a và vẽ đường thẳng vuông góc với trục này tại điểm a.
- Tìm trên trục tung điểm b và vẽ đường thẳng vuông góc với trục này tại điểm b.
- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm P cần tìm.
Chú ý: Trên mặt phẳng tọa độ, mỗi cặp số (a; b) xác định một điểm P duy nhất.
Ví dụ: Biểu diễn điểm M(2; -3) trên mặt phẳng tọa độ Oxy
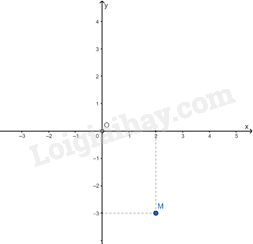
3. Đồ thị của hàm số
Đồ thị của hàm số y = f(x) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M(x; f(x)).
Ví dụ: Đồ thị của hàm số y = f(x) cho bởi bảng:
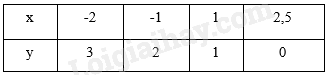
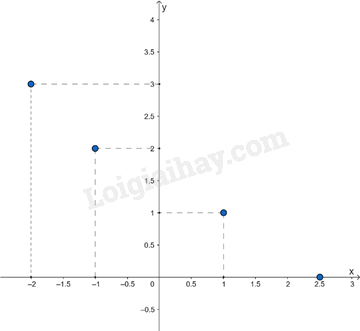
Sơ đồ tư duy Tọa độ của một điểm và đồ thị của hàm số
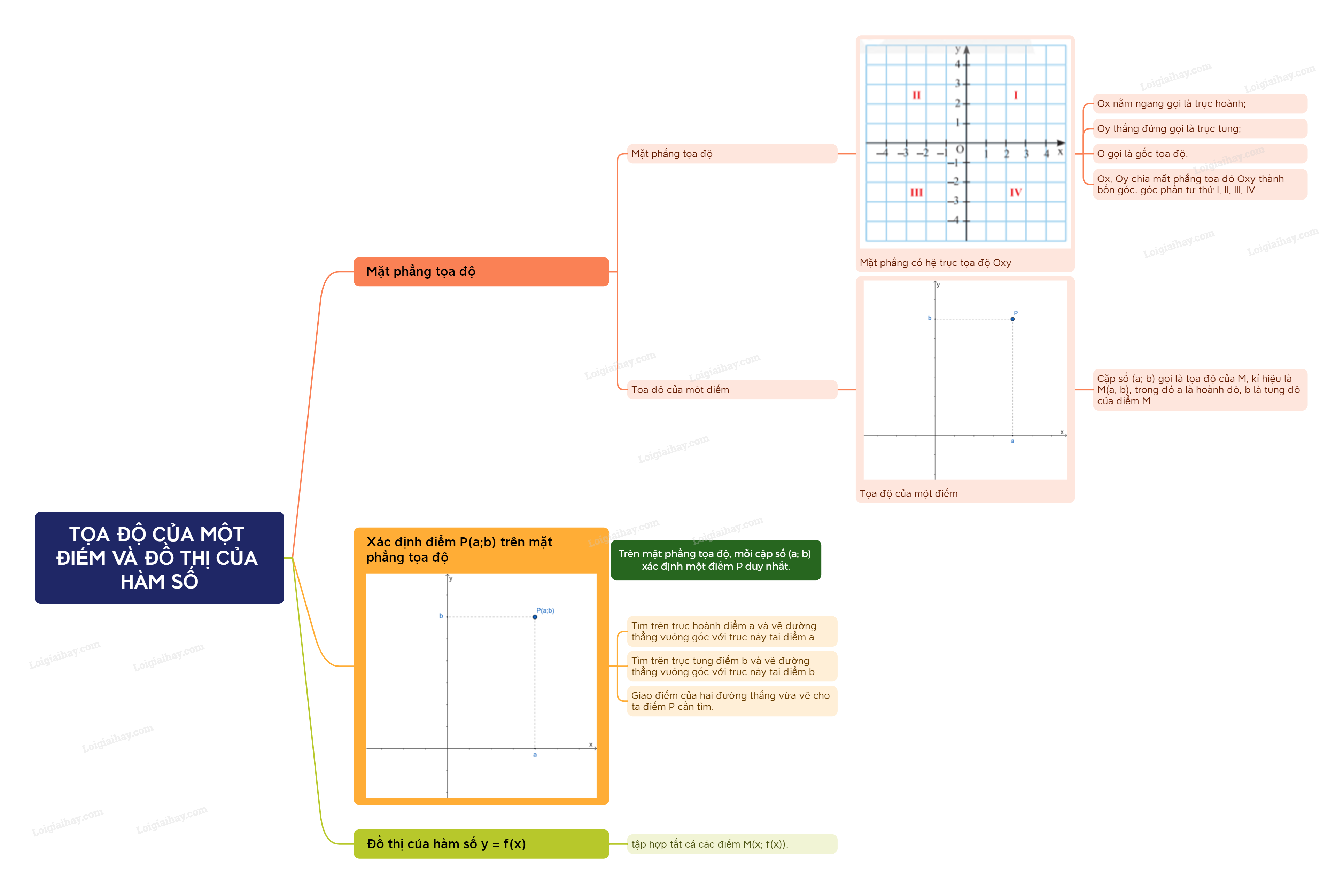
B. Bài tập Tọa độ của một điểm và đồ thị của hàm số
Đang cập nhật...
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 1: Khái niệm hàm số
Lý thuyết Bài 2: Tọa độ của một điểm và đồ thị của hàm số
Lý thuyết Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)
Lý thuyết Bài 4: Hệ số góc của đường thẳng
Lý thuyết Bài 1: Phương trình bậc nhất một ẩn
Lý thuyết Bài 2: Giải bài toán bằng cách lập phương trình bậc nhất