Với giải sách bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 1: Hai đường thẳng vuông góc
Giải SBT Toán 11 trang 88
a) Số đo giữa hai đường thẳng AB và B’C’ bằng:
A. 30°;
B. 45°;
C. 60°;
D. 90°.
b) Số đo giữa hai đường thẳng AB và CC’ bằng:
A. 30°;
B. 45°;
C. 60°;
D. 90°.
c) Số đo giữa hai đường thẳng AM và A’C’ bằng:
A. 30°;
B. 45°;
C. 60°;
D. 90°.
Lời giải:
a) Đáp án đúng là: C
Do tam giác ABC đều nên .
Ta có: BC // B’C’ nên .
b) Đáp án đúng là: D
Do ABB’A là hình chữ nhật nên .
Ta có: BB’ // CC’ nên .
c) Đáp án đúng là: A
Do tam giác ABC đều, AM là đường trung tuyến nên AM cũng là đường phân giác của .
Suy ra: .
Ta có: AC // A’C’ nên .
Lời giải:
Ba cặp đường thẳng vuông góc với nhau có thể là: a và b, b và c, c và d.
Bài 3 trang 89 SBT Toán 11 Tập 2: Cho hình hộp ABCD.A’B’C’D’ có đáy là hình vuông.
a) Chứng minh rằng AB ⊥ A’D’ và AC ⊥ B’D’.
b) Tính góc giữa hai đường thẳng AC và A’B’.
Lời giải:
a) ⦁ Do ABCD.A’B’C’D’ là hình hộp nên A’D’ // AD (tính chất hình hộp).
Mà AB ⊥ AD (vì ABCD là hình vuông)
Từ đó, suy ra AB ⊥ A’D’.
⦁ Do ABCD.A’B’C’D’ là hình hộp nên ta có BB’ // DD’ và BB’ = DD’.
Suy ra B’D’DB là hình bình hành nên ta có B’D’ // BD.
Mà AC ⊥ BD (vì ABCD là hình vuông)
Từ đó, suy ra AC ⊥ B’D’.
b) Xét hình vuông ABCD có: .
Mà AB // A’B’ nên .
Vậy góc giữa hai đường thẳng AC và A’B’ bằng 45°.
Lời giải:
Do MNPQ.M’N’P’Q’ là hình lăng trụ có tất cả các cạnh bằng nhau nên PQ = QQ’ = P’Q’ = PP’. Suy ra PQQ’P’ là hình thoi nên có: P’Q ⊥ PQ’. (1)
Tương tự: ta cũng có M’Q’QM và MQPN là hai hình thoi.
Suy ra:
⦁ NP // MQ mà MQ // M’Q’ nên NP // M’Q’.
⦁ NP = MQ mà MQ = M’Q’ nên NP = M’Q’.
Từ đó, ta có: NPQ’M’ là hình bình hành, suy ra M’N // PQ’. (2)
Từ (1), (2) ta có: M’N ⊥ P’Q.
Lời giải:
Gọi O là trung điểm AC.
Do O, M lần lượt là trung điểm AC và AB nên OM là đường trung bình của tam giác ABC.
và OM // BC.
Tương tự ta có: ON là đường trung bình của tam giác ACD.
và ON // AD.
Khi đó: (AD, BC) = (ON, OM).
Xét tam giác MON, theo hệ quả định lí Cosin ta có:
.
Nên .
Suy ra: .
Vậy góc giữa hai đường thẳng AD và BC là 60°.
Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Hai đường thẳng vuông góc
Bài 2: Đường thẳng vuông góc với mặt phẳng
Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 4: Hai mặt phẳng vuông góc
Lý thuyết Hai đường thẳng vuông góc
1. Góc giữa hai đường thẳng trong không gian
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu (a, b) hoặc .
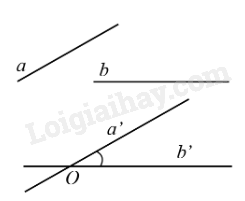
Nhận xét:
- Góc giữa hai đường thẳng a, b không phụ thuộc vào vị trí điểm O. Thông thường, khi tìm góc giữa hai đường thẳng a, b, ta chọn O thuộc a hoặc O thuộc b.
- Góc giữa hai đường thẳng a, b bằng góc giữa hai đường thẳng b, a, tức là (a, b) = (b, a).
- Góc giữa hai đường thẳng không vượt quá .
- Nếu a // b thì (a, c) = (b, c) với mọi đường thẳng c trong không gian.
2. Hai đường thẳng vuông góc trong không gian
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng .
Khi hai đường thẳng a và b vuông góc với nhau, ta kí hiệu .
Nhận xét: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.