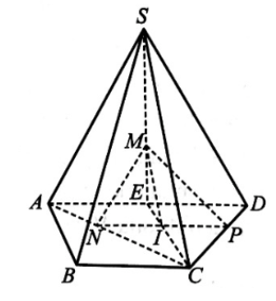
Gọi E là trung điểm của AD và I là giao điểm của NP và EC.

Ta có $\frac{AN}{AC}=\frac{DP}{DC}=\frac{1}{3}$ nên NP // AD.

Do AD // BC (ABCD là hình thang có AD là đáy) nên NP // BC.

Mà BC ⊂ (SBC). Suy ra NP // (SBC). (1)

Vì NP // AD nên ta có $\frac{EI}{EC}=\frac{AN}{AC}=\frac{1}{3}$.

Do M là trọng tâm của tam giác SAD và E trung điểm của đoạn AD nên M ∈ SE và $\frac{EM}{ES}=\frac{1}{3}$.

Như vậy $\frac{EI}{EC}=\frac{EM}{ES}$ nên MI // SC.

Mà SC ⊂ (SBC). Suy ra MI // (SBC). (2)

Lại có MI và NP là hai đường thẳng cắt nhau tại I trong mặt phẳng (MNP). (3)

Từ (1), (2) và (3) suy ra (MNP) // (SBC).

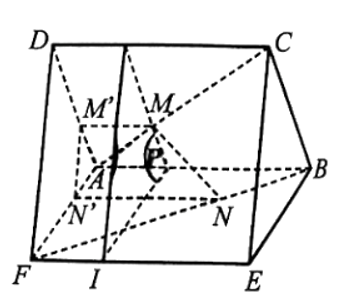
a) Ta có MM' // AB và NN' // AB (theo đề bài) nên MM' // NN'.

Suy ra M, M', N', N cùng thuộc một mặt phẳng. (1)

Ta có CD // AB (do ABCD là hình bình hành) và EF // AB (do ABEF là hình bình hành) nên CD // EF, suy ra C, D, F, E cùng thuộc một mặt phẳng.

Do AB // CD nên MM' // CD, mà CD ⊂ (CDE), suy ra MM' // (CDE). (2)

Theo định lí Thalés trong tam giác ACD, ta có $\frac{AM}{AC}=\frac{AM\text{'}}{AD}$ (MM' // CD).

Tương tự, trong tam giác AFB có $\frac{BN}{BF}=\frac{AN\text{'}}{AF}$ (NN' // AB).

Mà $\frac{AM}{AC}=\frac{BN}{BF}$ (theo đề bài). Do đó, $\frac{AM\text{'}}{AD}=\frac{AN\text{'}}{AF}$, từ đó suy ra M'N' // DF.

Mà DF ⊂ (CDE) (do C, D, F, E cùng thuộc một mặt phẳng) nên M'N' // (CDE). (3)

Từ (2) và (3) suy ra (MM'N') // (CDE). (4)

Từ (1) và (4) suy ra (MNN') // (CDE).

b) Ta có AF // BE và AD // BC, từ đó suy ra (ADF) // (BCE).

Khi đó đường thẳng AC cắt ba mặt phẳng song song (ADF), (P), (BCE) lần lượt tại A, M, C; đường thẳng FE cũng cắt ba mặt phẳng trên theo thứ tự tại F, I, E.

Áp dụng định lí Thalés trong không gian, ta có: $\frac{AM}{FI}=\frac{MC}{IE}=\frac{AC}{FE}$.

Suy ra $\frac{FI}{FE}=\frac{AM}{AC}$. Mà $\frac{AM}{AC}=\frac{1}{3}$ nên $\frac{FI}{FE}=\frac{1}{3}$.