Với giải sách bài tập Toán 11 Bài 20: Hàm số mũ và hàm số lôgarit sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán lớp 11 Bài 20: Hàm số mũ và hàm số lôgarit
Bài 6.21 trang 14 SBT Toán 11 Tập 2: Vẽ đồ thị của các hàm số mũ sau:
a) ; b) .
Lời giải:
a) Lập bảng giá trị của hàm số tại một số điểm như sau:
Từ đó, ta vẽ được đồ thị của hàm số như hình sau:
b) Lập bảng giá trị của hàm số tại một số điểm như sau:
Từ đó, ta vẽ được đồ thị của hàm số như hình sau:
Bài 6.22 trang 14 SBT Toán 11 Tập 2: Vẽ đồ thị của các hàm số lôgarit sau:
a) ; b) .
Lời giải:
a) Lập bảng giá trị của hàm số tại một số điểm như sau:
Từ đó, ta vẽ được đồ thị của hàm số như hình sau:
b) Lập bảng giá trị của hàm số tại một số điểm như sau:
Từ đó, ta vẽ được đồ thị của hàm số như hình sau:
Bài 6.23 trang 14 SBT Toán 11 Tập 2: Cho hàm số mũ f(x) = ax (a > 0). Chứng minh rằng:
a) ;
b) ;
c) .
Lời giải:
a) Ta có .
b) Ta có .
c) Ta có .
Bài 6.24 trang 14 SBT Toán 11 Tập 2: Tìm tập xác định của các hàm số sau:
a) y = log3 (x + 1); b) .
Lời giải:
a) Điều kiện: x + 1 > 0 x > −1.
Vậy tập xác định của hàm số là (−1; +).
b) Điều kiện |x – 1| > 0 x ≠ 1.
Vậy tập xác định của hàm số là ℝ\{1}.
Bài 6.25 trang 14 SBT Toán 11 Tập 2: Cho hàm số lôgarit f(x) = loga x (0 < a ≠ 1). Chứng minh rằng:
a) ; b) f(x) = f(x).
Lời giải:
a) Ta có .
b) f(x) = loga x = loga x = f(x).
Bài 6.26 trang 14 SBT Toán 11 Tập 2: Ta định nghĩa các hàm sin hyperbolic và hàm côsin hyperbolic như sau:
.
Chứng minh rằng:
a) sinh x là hàm số lẻ;
b) cosh x là hàm số chẵn;
c) (cosh x)2 – (sinh x)2 = 1 với mọi x.
Lời giải:
a) Hàm số có tập xác định D = ℝ.
Ta có: ∀ x ∈ D ⇒ – x ∈ D.
Và , ∀ x ∈ ℝ.
Do đó, sinh x là hàm số lẻ.
b) Hàm số có tập xác định D = ℝ.
Ta có: ∀ x ∈ D ⇒ – x ∈ D.
Và , ∀ x ∈ ℝ.
Do đó, cosh x là hàm số chẵn.
c) Ta có: (cosh x)2 – (sinh x)2
.
Do đó, (cosh x)2 – (sinh x)2 = 1 với mọi x.
Bài 6.27 trang 15 SBT Toán 11 Tập 2: Nếu một ô kính ngăn khoảng 3% ánh sáng truyền qua nó thì phần trăm ánh sáng p truyền qua n ô kính liên tiếp được cho gần đúng bởi hàm số sau:
p (n) = 100 × (0,97)n.
a) Có bao nhiêu phần trăm ánh sáng sẽ truyền qua 10 ô kính?
b) Có bao nhiêu phần trăm ánh sáng sẽ truyền qua 25 ô kính?
(Kết quả ở câu a và câu b được làm tròn đến hàng đơn vị).
Lời giải:
a) Phần trăm ánh sáng sẽ truyền qua 10 ô kính là: p (10) = 100.(0,97)10 74%.
Vậy khoảng 74% ánh sáng sẽ truyền qua 10 ô kính.
b) Phần trăm ánh sáng sẽ truyền qua 25 ô kính là: p (25) = 100.(0,97)25 47%.
Vậy khoảng 47% ánh sáng sẽ truyền qua 25 ô kính.
Bài 6.28 trang 15 SBT Toán 11 Tập 2: Số tiền ban đầu 120 triệu đồng được gửi tiết kiệm với lãi suất năm không đổi là 6%. Tính số tiền (cả vốn lẫn lãi) thu được sau 5 năm nếu nó được tính lãi kép:
a) hằng quý;
b) hằng tháng;
c) liên tục.
(Kết quả được tính theo đơn vị triệu đồng và làm tròn đến chữ số thập phân thứ ba).
Lời giải:
Chú ý:
- Công thức lãi kép theo định kì để tính tổng số tiền thu được , trong đó P là số tiền vốn ban đầu, r là lãi suất năm (r cho dưới dạng số thập phân), n là số kì tính lãi trong một năm và t là số kì gửi.
- Công thức tính lãi kép liên tục A = Pert, trong đó r là lãi suất năm (r cho dưới dạng số thập phân) và t là số năm gửi tiết kiệm.
a) Áp dụng công thức với P = 120, r = 6% = 0,06, n = 4, t = 20, ta được số tiền (cả vốn lẫn lãi) thu được sau 5 năm nếu nó được tính lãi kép hằng quý là:
(triệu đồng).
Vậy số tiền (cả vốn lẫn lãi) thu được sau 5 năm nếu nó được tính lãi kép hằng quý khoảng 161,623 triệu đồng.
b) Áp dụng công thức với P = 120, r = 6% = 0,06, n = 12, t = 60, ta được số tiền (cả vốn lẫn lãi) thu được sau 5 năm nếu nó được tính lãi kép hằng tháng là:
(triệu đồng).
Vậy số tiền (cả vốn lẫn lãi) thu được sau 5 năm nếu nó được tính lãi kép hằng tháng khoảng 161,862 triệu đồng.
c) Áp dụng công thức tính lãi kép liên tục A = Pert với P = 120, r = 6% = 0,06, t = 5, ta được số tiền (cả vốn lẫn lãi) thu được sau 5 năm nếu nó được tính lãi kép liên tục là:
A = 120 . e0,06.5 = 120 . e0,3 161,983 (triệu đồng).
Vậy số tiền (cả vốn lẫn lãi) thu được sau 5 năm nếu nó được tính lãi kép liên tục khoảng 161,983 triệu đồng.
Bài 6.29 trang 15 SBT Toán 11 Tập 2: Chu kì bán rã của đồng vị phóng xạ Radi 226 là khoảng 1 600 năm. Giả sử khối lượng m (tính bằng gam) còn lại sau t năm của một lượng Radi 226 được cho bởi công thức:
.
a) Khối lượng ban đầu (khi t = 0) của lượng Radi 226 đó là bao nhiêu?
b) Sau 2 500 năm khối lượng của lượng Radi 226 đó là bao nhiêu?
Lời giải:
a) Khối lượng ban đầu (khi t = 0) của lượng Radi 226 đó là: (g).
Vậy khối lượng ban đầu (khi t = 0) của lượng Radi 226 đó là 25 gam.
b) Sau 2 500 năm (t = 2 500) khối lượng của lượng Radi 226 đó là:
(g).
Vậy sau 2 500 năm khối lượng của lượng Radi 226 đó khoảng 8,46 gam.
Bài 6.30 trang 15 SBT Toán 11 Tập 2: Trong Vật lí, mức cường độ âm (tính bằng deciben, kí hiệu là dB) được tính bởi công thức , trong đó I là cường độ âm tính theo W/m2 và I0 = 10−12 W/m2 là cường độ âm chuẩn, tức là cường độ âm thấp nhất mà tai người có thể nghe được.
a) Tính mức cường độ âm của một cuộc trò chuyện bình thường có cường độ âm là 10−7 W/m2 .
b) Khi cường độ âm tăng lên 1 000 lần thì mức cường độ âm (đại lượng đặc trưng cho độ to nhỏ của âm) thay đổi thế nào?
Lời giải:
a) Mức cường độ âm của một cuộc trò chuyện bình thường có cường độ âm 10−7 W/m2 là: (dB).
Vậy mức cường độ âm của một cuộc trò chuyện bình thường có cường độ âm 10−7 W/m2 là 50 dB.
b) Khi cường độ âm tăng lên 1 000 lần, ta có mức cường độ âm
.
Vậy mức cường độ âm tăng lên 30 dB khi cường độ âm tăng lên 1 000 lần.
Xem thêm các bài giải SBT Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 22: Hai đường thẳng vuông góc
Bài 23: Đường thẳng vuông góc với mặt phẳng
Lý thuyết Hàm số mũ và hàm số lôgarit
1. Hàm số mũ
a) Khái niệm hàm số mũ
Cho a là số thực dương khác 1.
Hàm số được gọi là hàm số mũ cơ số a.
b) Đồ thị và tính chất của hàm số mũ
Hàm số mũ :
- Có tập xác định là và tập giá trị là ;
- Đồng biến trên khi a > 1 và nghịch biến trên khi 0 < a < 1;
- Liên tục trên ;
- Có đồ thị đi qua các điểm (0; 1), (1; a) và luôn nằm phía trên trục hoành.
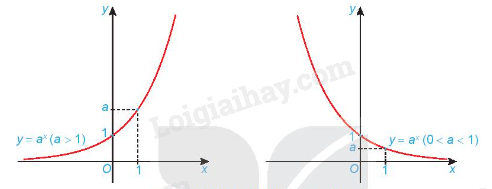
Dạng đồ thị của hàm số
2. Hàm số lôgarit
a) Khái niệm hàm số lôgarit
Cho a là số thực dương khác 1.
Hàm số được gọi là hàm số lôgarit cơ số a.
b) Đồ thị và tính chất của hàm số lôgarit
Hàm số lôgarit :
- Có tập xác định là và tập giá trị là ;
- Đồng biến trên khi a > 1 và nghịch biến trên khi 0 < a < 1;
- Có đồ thị đi qua các điểm (1; 0), (a; 1) và luôn nằm bên phải trục tung.
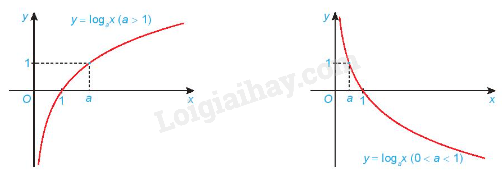
Dạng đồ thị của hàm số