Với tóm tắt lý thuyết Toán lớp 6 Bài 2: Tập hợp các số nguyên sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 2: Tập hợp các số nguyên

Video giải Toán 6 Bài 2: Tập hợp các số nguyên - Cánh diều

A. Lý thuyết Tập hợp các số nguyên

I. Tập hợp các số nguyên

+ Số tự nhiên khác 0 còn được gọi là số nguyên dương.

+ Các số nguyên âm, số 0 và các số nguyên dương tạo thành tập hợp các số nguyên.

+ Tập hợp các số nguyên được kí hiệu là .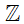

Ví dụ: 

+ Các số nguyên dương: 4, 6, 10 000, … 

+ Tập hợp các số nguyên 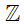= {…, – 2, – 1, 0, 1, 2, …}

Chú ý:

+ Số 0 không phải số nguyên âm, cũng không phải số nguyên dương.

+ Các số nguyên dương 1, 2, 3,... đều mang dấu “+" nên còn được viết là + 1, + 2, + 3,...

II. Biểu diễn số nguyên trên trục số 

Ta có thể biểu diễn số nguyên trên trục số. Có hai loại trục số:

1. Trục số nằm ngang 

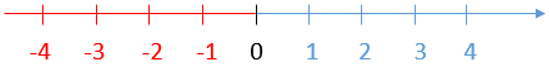
Trên trục số nằm ngang, điểm biểu diễn số nguyên âm nằm bên trái điểm 0, điểm biểu diễn số nguyên dương nằm bên phải điểm 0.

2. Trục số thẳng đứng

Trên trục số thẳng đứng, điểm biểu diễn số nguyên âm nằm phía dưới điểm 0, điểm biểu diễn số nguyên dương nằm phía trên điểm 0.

Chú ý: Khi nói “trục số” mà không nói gì thêm, ta hiểu là nói về trục số nằm ngang.

III. Số đối của một số nguyên 

+ Trên trục số, hai số nguyên (phân biệt) có điểm biểu diễn nằm về hai phía của gốc 0 và cách đều gốc 0 được gọi là hai số đối nhau.

+ Số đối của 0 là 0.

Ví dụ: 

– 4 và 4 là hai số đối nhau.

– 4 là số đối của 4 và 4 là số đối của – 4.

IV. So sánh các số nguyên

1. So sánh hai số nguyên

+ Trên trục số nằm ngang, nếu điểm a nằm bên trái điểm b thì số nguyên a nhỏ hơn số nguyên b.

+ Trên trục số thẳng đứng, nếu điểm a nằm phía dưới điểm b thì số nguyên a nhỏ hơn số nguyên b.

+ Nếu a nhỏ hơn b thì ta viết là a < b hoặc b > a.

Ví dụ: 

Điểm – 10 nằm bến trái điểm – 5 nên – 10 < – 5 

Điểm 2 nằm bên phải điểm 0 nên 2 > 0.

Chú ý: 

+ Số nguyên dương luôn lớn hơn 0. Số nguyên âm luôn nhỏ hơn 0.

+ Nếu a < b và b < c thì a < c

Ví dụ: – 2 < 0 và 0 < 5 thì – 2 < 5. 

2. Cách so sánh hai số nguyên

2.1 So sánh hai số nguyên khác dấu

Số nguyên âm luôn nhỏ hơn số nguyên dương. 

Ví dụ: – 7 là số nguyên âm và 5 là số nguyên dương nên – 7 < 5. 

2.2 So sánh hai số nguyên cùng dấu

+ So sánh hai số nguyên dương: Đã biết ở chương I.

+ So sánh hai số nguyên âm:

Để so sánh hai số nguyên âm, ta làm như sau:

Bước 1. Bỏ dấu “–” trước cả hai số âm

Bước 2. Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (trước khi bỏ dấu “–”) sẽ lớn hơn. 

Ví dụ: So sánh – 216 và – 309.

Bỏ dấu “–” trước các số – 216 và – 309, ta được các số lần lượt là 216 và 309.

Do 216 < 309 nên – 216 > – 309. 

B. Bài tập tự luyện

Bài 1. Viết các số sau theo thứ tự giảm dần: – 154, – 618, – 219, 58.

Lời giải:

+ Vì số nguyên dương luôn lớn hơn số nguyên âm, nên trong các số đã cho ta có 58 là số lớn nhất.

+ Ta so sánh các số nguyên âm: – 154, – 618, – 219

Bỏ dấu “–” trước các số – 154, – 618, – 219 ta được các số lần lượt là 154, 618, 219.

Do 154 < 219 < 618 nên – 154 > – 219 > – 618 

Do đó ta có: 58 > – 154 > – 219 > – 618.

Vậy sắp xếp các số đã cho theo thứ tự giảm dần ta được: 58, – 154, – 219, – 618. 

Bài 2. Chọn kí hiệu "∈”, "∉" thích hợp cho  :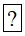

a) -3 

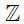
b) 0  

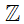
c) 4 

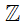
d) -2  

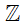
Lời giải:

a) Ta có số – 3 là số nguyên âm nên nó thuộc tập hợp các số nguyên.

Do đó ta viết -3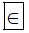 

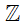
b) Ta có số 0 là số nguyên nên nó thuộc tập hợp các số nguyên.

Do đó ta viết 0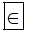 

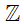
c) Ta có số 4 là số nguyên dương nên nó cũng thuộc tập hợp các số nguyên. 

Do đó ta viết 4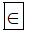 

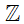
d) Ta có số – 2 là số nguyên âm nên nó không phải là số tự nhiên hay – 2 không thuộc tập hợp các số tự nhiên.

Do đó ta viết  -2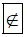 

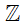
Bài 3. So sánh các cặp số sau: 3 và 5; – 1 và – 3; – 5 và 2; 5 và – 3.

Lời giải:

Ta có thể so sánh các cặp số trên bằng một trong các cách sau:

Cách 1. 

Biểu diễn các số đã cho lên trục số ta được:

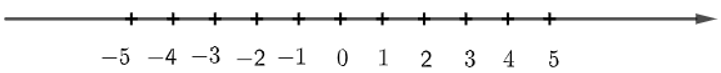
+) Ta thấy điểm 3 nằm bên trái điểm 5 nên 3 < 5.

+) Điểm – 3 nằm bên trái điểm – 1 nên – 3 < – 1 hay – 1 > – 3.

+) Điểm – 5 nằm bên trái điểm 2 nên – 5 < 2. 

+) Điểm – 3 nằm bên trái điểm 5 nên – 3 < 5 hay 5 > – 3.

Cách 2. 

+) Ta có: 3 < 5 (so sánh hai số tự nhiên)

+) So sánh – 1 và – 3

Bỏ dấu “–” trước các số – 1 và – 3 ta được các số lần lượt là 1 và 3. 

Do 1 < 3 nên – 1 > – 3.

+) So sánh – 5 và 2 

Vì – 5 là số nguyên âm và 2 là số nguyên dương nên – 5 < 2. 

+) So sánh 5 và – 3

Vì 5 là số nguyên dương và – 3 là số nguyên âm nên 5 > – 3. 

Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Số nguyên âm

Lý thuyết Bài 2: Tập hợp các số nguyên

Lý thuyết Bài 3: Phép cộng các số nguyên

Lý thuyết Bài 4: Phép trừ số nguyên. Quy tắc dấu ngoặc

Lý thuyết Bài 5: Phép nhân các số nguyên