Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Thứ tự trong tập hợp số nguyên được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Thứ tự trong tập hợp số nguyên. Mời các bạn đón xem:
Bài tập Toán 6 Thứ tự trong tập hợp số nguyên
A. Bài tập Thứ tự trong tập hợp số nguyên
Bài 1. Viết các số sau theo thứ tự giảm dần: – 154, – 618, – 219, 58.
Lời giải:
+ Vì số nguyên dương luôn lớn hơn số nguyên âm, nên trong các số đã cho ta có 58 là số lớn nhất.
+ Ta so sánh các số nguyên âm: – 154, – 618, – 219
Bỏ dấu “–” trước các số – 154, – 618, – 219 ta được các số lần lượt là 154, 618, 219.
Do 154 < 219 < 618 nên – 154 > – 219 > – 618
Do đó ta có: 58 > – 154 > – 219 > – 618.
Vậy sắp xếp các số đã cho theo thứ tự giảm dần ta được: 58, – 154, – 219, – 618.
Bài 2. Chọn kí hiệu "∈”, "∉" thích hợp cho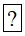 
:
a) -3 
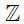
b) 0 
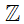
c) 4 
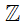
d) -2 
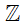
Lời giải:
a) Ta có số – 3 là số nguyên âm nên nó thuộc tập hợp các số nguyên.
Do đó ta viết -3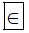 
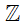
b) Ta có số 0 là số nguyên nên nó thuộc tập hợp các số nguyên.
Do đó ta viết 0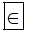 
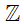
c) Ta có số 4 là số nguyên dương nên nó cũng thuộc tập hợp các số nguyên.
Do đó ta viết 4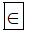 
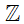
d) Ta có số – 2 là số nguyên âm nên nó không phải là số tự nhiên hay – 2 không thuộc tập hợp các số tự nhiên.
Do đó ta viết -2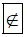 
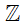
Bài 3. So sánh các cặp số sau: 3 và 5; – 1 và – 3; – 5 và 2; 5 và – 3.
Lời giải:
Ta có thể so sánh các cặp số trên bằng một trong các cách sau:
Cách 1.
Biểu diễn các số đã cho lên trục số ta được:
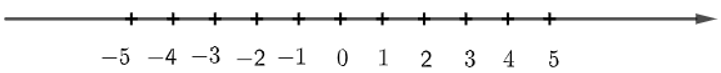
+) Ta thấy điểm 3 nằm bên trái điểm 5 nên 3 < 5.
+) Điểm – 3 nằm bên trái điểm – 1 nên – 3 < – 1 hay – 1 > – 3.
+) Điểm – 5 nằm bên trái điểm 2 nên – 5 < 2.
+) Điểm – 3 nằm bên trái điểm 5 nên – 3 < 5 hay 5 > – 3.
Cách 2.
+) Ta có: 3 < 5 (so sánh hai số tự nhiên)
+) So sánh – 1 và – 3
Bỏ dấu “–” trước các số – 1 và – 3 ta được các số lần lượt là 1 và 3.
Do 1 < 3 nên – 1 > – 3.
+) So sánh – 5 và 2
Vì – 5 là số nguyên âm và 2 là số nguyên dương nên – 5 < 2.
+) So sánh 5 và – 3
Vì 5 là số nguyên dương và – 3 là số nguyên âm nên 5 > – 3.
Câu 4. Khẳng định nào sau đây đúng?
A. Nếu x < 3 thì x < 1
B. Nếu x > 3 thì x > 5
C. Nếu x > 2 thì x > −1
D. Nếu x < 8 thì x < 5
Trả lời:
Do x > 2 và 2 > −1 nên x > −1.
Đáp án cần chọn là: C
Câu 5. Nếu a là số nguyên dương thì:
A. a ≥ 0
B. a > 0
C. a < 0
D. a ≤ 0
Trả lời:
Nếu a là số nguyên dương thì: a > 0.
Đáp án cần chọn là: B
Câu 6. Số liền sau của số −5 là số
A. 4
B. −6
C. −4
D. −5
Trả lời:
Ta thấy: −5 < −4 và không có số nguyên nào nằm giữa −5 và −4
Nên số liền sau của số −5là số −4.
Đáp án cần chọn là: C
Câu 7. Chọn câu đúng.
A. 2 > 3
B. 3 < −2
C. 0 < −3
D. −4 < −3
Trả lời:
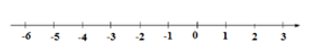
Điểm 2 nằm bên trái điểm 3 nên 2 < 3. Do đó A sai.
Điểm 3 nằm bên phải điểm −2 nên 3 > −2. Do đó B sai
Điểm 0 nằm bên trái điểm −3 nên 0 > − 3. Do đó C sai
Điểm −4 nằm bên trái điểm −3 nên−4 < −3. Do đó D đúng
Đáp án cần chọn là: D
Câu 8. Số nguyên âm lớn nhất có 6 chữ số là
A. −1000000
B. −10000
C. −100000
D. 100000
Trả lời:
Số nguyên dương nhỏ nhất có 6 chữ số là: 100000
Nên số nguyên âm lớn nhất có 6 chữ số là: −100000
Đáp án cần chọn là: C
Câu 9. Khẳng định nào dưới đây đúng?
A. Số nguyên a lớn hơn −4. Số aa chắc chắn là số dương.
B. Số nguyên a nhỏ hơn 3. Số aa chắc chắn là số âm.
C. Số nguyên a lớn hơn 1. Số aa chắc chắn là số dương.
D. Số nguyên a nhỏ hơn 0. Số aa có thể là số dương, có thể là số âm
Trả lời:
Phương án A sai. Ví dụ −2 > −4 nhưng −2 là số nguyên âm.
Phương án B sai. Ví dụ 1 < 3 nhưng 1 là số dương.
Phương án D sai vì các số nguyên nhỏ hơn 0 là các số nguyên âm.
Phương án C đúng.
Đáp án cần chọn là: C
Câu 10. Trong các khẳng định sau, khẳng định nào đúng?
A. −46718 < −46812
B. −67523 < −66712
C. −12 > 7
D. −123 < −126
Trả lời:
Do 67523 > 66712 nên −67523 < −66712
Khẳng định đúng là: B
Đáp án cần chọn là: B
Câu 11. Hãy sắp xếp các số sau theo thứ tự tăng dần -3; +4; 7; -7; 0; -1; +15; -8; 25.
A. −8; −7; −3; −1; 0; +4; 7; +15; 25.
B. 0; +4; 7; +15; 25, −8; −7; −3; −1;
C. 0; −1; −3; +4; −7; 7; −8; +15; 25
D. 25; +15; 7; +4; 0; −1; −3; −7; −8
Trả lời:
−8 < −7 < −3 < −10 < +4 < 7 < +15 < 25.
Các số được sắp xếp theo thứ tự tăng dần là:−8; −7; −3; −1; 0; +4; 7; +15; 25.
Đáp án cần chọn là: A
Câu 12. Sắp xếp các số sau theo thứ tự tăng dần: −2021;4;0;−10;−1
A. −2021;−10;4;0;−1
B. −2021;−10;−1;0;4
C. −2021;−10;0;−1;4
D. 4;0;−1;−10;−2021
Trả lời:
Ta có: −2021 < −10 < −1 < 0 < 4
Sắp xếp theo thứ tự tăng dần: −2021; −10; −1; 0; 4
Đáp án cần chọn là: B
Câu 13. Một sinh vật biển sống gần mặt nước, trong khi đó một số khác lại sống rất sâu dưới đáy đại dương. Hãy sắp xếp các sinh vật biển sau theo thứ tự giảm dần độ cao của môi trường sống.
A. Cá cờ xanh, Sao biển, Cá hố, Cá đèn
B. Sao biển, Cá đèn, Cá hố, Cá cờ xanh
C. Cá cờ xanh, Cá hố, Sao biển, Cá đèn.
D. Cá cờ xanh, Cá hố, Cá đèn, Sao biển.
Trả lời:
180 < 1000 < 4000 < 6000
⇒−180 > −1000 > −4000 > −6000
Sắp xếp theo thứ tự giảm dần độ cao của môi trường sống:
Cá cờ xanh, Cá hố, Cá đèn, Sao biển.
Đáp án cần chọn là: D
Câu 14. Nhiệt độ (0C) mùa đông tại các địa điểm sau đây của nước Mĩ:
Hawaii (Ha-oai) 120C;
Montana (Môn-ta-na) −20C;
Alaska (A-la-xca)−510 C;
New York (Niu- Oóc) −150 C;
Florida (Phlo-ri-đa) 80C.
Sắp xếp các thành phố theo thứ tự từ thấp đến cao về nhiệt độ?
A. Hawaii, Montana, New York, Alaska, Florida.
B. Alaska, New York, Montana, Florida, Hawaii.
C. Alaska, New York, Florida, Hawaii, Montana.
D. Hawaii, Florida, Montana, New York, Alaska.
Trả lời:
51 > 15 > 2 ⇒ −51 < −15 < −2
Sắp xếp nhiệt độ theo thứ tự từ thấp đến cao:
-510C; -150C; -20C; 80C; 120C
Sắp xếp các thành phố theo thứ tự từ thấp đến cao về nhiệt độ:
Alaska, New York, Montana, Florida, Hawaii.
Đáp án cần chọn là: B
Câu 15. Liệt kê các phần tử của tập hợp sau theo thứ tự giảm dần:
A ={x∈Z|−1 < x ≤ 3}
A. {−1;0;1;2;3}
B. {−1;0;1;2}
C. {0;1;2;3}
D. {3;2;1;0}
Trả lời:
Ta có: A ={0;1;2;3}
Do 3 > 2 > 1 > 0 nên thứ tự giảm dần các phần tử là: {3; 2; 1; 0}
Đáp án cần chọn là: D
Câu 16. Chọn câu sai
A. −5 < −2
B. 0 < 4
C. 0 > −1
D. −5 < −6
Trả lời:
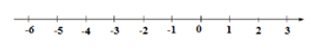
Điểm −5 nằm bên trái điểm −2 nên −5 < −2. Do đó A đúng.
Điểm 0 nằm bên trái điểm 4 nên 0 < 4. Do đó B đúng.
Điểm 0 nằm bên phải điểm −1 nên 0 > −1. Do đó C đúng.
Điểm −5 nằm bên phải điểm −6 nên −5 > −6 Do đó D sai.
Đáp án cần chọn là: D
Câu 17. Số liền trước của số −19là số
A. 20
B. −17
C. −18
D. −20
Trả lời:
Ta thấy: −20 < −19 và không có số nguyên nào nằm giữa −20 và −19.
Nên số liền trước của số−19 là số −20.
Đáp án cần chọn là: D
Câu 18. Biết −9 < x < 0. Tập hợp các số nguyên xx thỏa mãn:
A. A ={−8;−7;−6;−5;−4;−3;−2;−1}
B. A ={−9;−8;−7;−6;−5;−4;−3;−2;−1}
C. A ={−9;−8;−7;−6;−5;−4;−3;−2;−1;0}
D. A ={−8;−7;−6;−5;−4;−3;−2;−1;0}
Trả lời:
Vì−9 < x < 0; x∈Z ⇒ x∈{−8;−7;−6;−5;−4;−3;−2;−1}
Do đó A={−8;−7;−6;−5;−4;−3;−2;−1}
Đáp án cần chọn là: A
Câu 19. Số liền trước của số đối của số 11là
A. −12
B. −11
C. −10
D. 12
Trả lời:
Số đối của số 11 là: −11
Số liền trước của −11 là: −12
Đáp án cần chọn là: A
Câu 20. Tìm các giá trị thích hợp của chữ số a sao cho:
A. 6
B. 5
C. 4
D. 7
Trả lời:
Mànên a = 5
Đáp án cần chọn là: B
B. Lý thuyết Thứ tự trong tập hợp số nguyên
I. Tập hợp các số nguyên
+ Số tự nhiên khác 0 còn được gọi là số nguyên dương.
+ Các số nguyên âm, số 0 và các số nguyên dương tạo thành tập hợp các số nguyên.
+ Tập hợp các số nguyên được kí hiệu là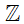 
.
Ví dụ:
+ Các số nguyên dương: 4, 6, 10 000, …
+ Tập hợp các số nguyên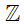 
= {…, – 2, – 1, 0, 1, 2, …}
Chú ý:
+ Số 0 không phải số nguyên âm, cũng không phải số nguyên dương.
+ Các số nguyên dương 1, 2, 3,... đều mang dấu “+" nên còn được viết là + 1, + 2, + 3,...
II. Biểu diễn số nguyên trên trục số
Ta có thể biểu diễn số nguyên trên trục số. Có hai loại trục số:
1. Trục số nằm ngang
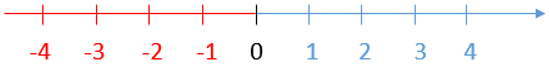
Trên trục số nằm ngang, điểm biểu diễn số nguyên âm nằm bên trái điểm 0, điểm biểu diễn số nguyên dương nằm bên phải điểm 0.
2. Trục số thẳng đứng
Trên trục số thẳng đứng, điểm biểu diễn số nguyên âm nằm phía dưới điểm 0, điểm biểu diễn số nguyên dương nằm phía trên điểm 0.
Chú ý: Khi nói “trục số” mà không nói gì thêm, ta hiểu là nói về trục số nằm ngang.
III. Số đối của một số nguyên
+ Trên trục số, hai số nguyên (phân biệt) có điểm biểu diễn nằm về hai phía của gốc 0 và cách đều gốc 0 được gọi là hai số đối nhau.
+ Số đối của 0 là 0.
Ví dụ:
– 4 và 4 là hai số đối nhau.
– 4 là số đối của 4 và 4 là số đối của – 4.
IV. So sánh các số nguyên
1. So sánh hai số nguyên
+ Trên trục số nằm ngang, nếu điểm a nằm bên trái điểm b thì số nguyên a nhỏ hơn số nguyên b.
+ Trên trục số thẳng đứng, nếu điểm a nằm phía dưới điểm b thì số nguyên a nhỏ hơn số nguyên b.
+ Nếu a nhỏ hơn b thì ta viết là a < b hoặc b > a.
Ví dụ:
Điểm – 10 nằm bến trái điểm – 5 nên – 10 < – 5
Điểm 2 nằm bên phải điểm 0 nên 2 > 0.
Chú ý:
+ Số nguyên dương luôn lớn hơn 0. Số nguyên âm luôn nhỏ hơn 0.
+ Nếu a < b và b < c thì a < c
Ví dụ: – 2 < 0 và 0 < 5 thì – 2 < 5.
2. Cách so sánh hai số nguyên
2.1 So sánh hai số nguyên khác dấu
Số nguyên âm luôn nhỏ hơn số nguyên dương.
Ví dụ: – 7 là số nguyên âm và 5 là số nguyên dương nên – 7 < 5.
2.2 So sánh hai số nguyên cùng dấu
+ So sánh hai số nguyên dương: Đã biết ở chương I.
+ So sánh hai số nguyên âm:
Để so sánh hai số nguyên âm, ta làm như sau:
Bước 1. Bỏ dấu “–” trước cả hai số âm
Bước 2. Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (trước khi bỏ dấu “–”) sẽ lớn hơn.
Ví dụ: So sánh – 216 và – 309.
Bỏ dấu “–” trước các số – 216 và – 309, ta được các số lần lượt là 216 và 309.
Do 216 < 309 nên – 216 > – 309.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
