Với giải sách bài tập Toán 6 Bài 2: Tập hợp các số nguyên sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 2: Tập hợp các số nguyên
Bài 8 trang 73 sách bài tập Toán lớp 6 Tập 1: Chọn kí hiệu '' ∈ '', '' ∉ '' thích hợp cho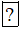 
:
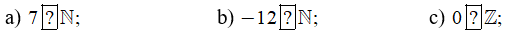
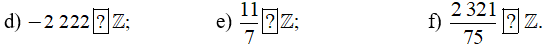
Lời giải:
a) Vì 7 là số tự nhiên nên 7 thuộc tập N, ta viết 7 
N
b) – 12 là số nguyên âm nên không thuộc tập N, ta viết -12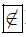 
N
c) Vì 0 là số nguyên nên 0 thuộc tập Z, ta viết 0 
Z
d) – 2 222 là số nguyên âm nên thuộc tập Z, ta viết -2 222 
Z
e) Vì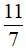 
không là số nguyên nên 
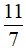không thuộc tập Z, ta viết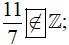 
f) Vì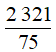 
không là số nguyên nên 
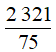không thuộc tập Z, ta viết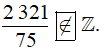 
Lời giải:
Do tập hợp số nguyên bao gồm các số nguyên âm, số 0 và các số nguyên dương nên phát biểu của bạn An còn thiếu số 0. Do đó phát biểu của bạn An là sai.
Bài 10 trang 73 sách bài tập Toán lớp 6 Tập 1:
a) Trong các số sau: -21; 321; -11 211; 0;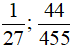
; -955 967 số nào không là số nguyên âm.
b) Trong các số sau: -17; -539; 666; 5 145; 987 652; -543 689, số nào không là số nguyên dương.
Lời giải:
a) Trong các số đã cho, các số không là số nguyên âm là: 321; 0;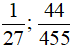 
b) Trong các số đã cho, các số không là số nguyên dương là: -17; -539; -543 689.
Bài 11 trang 73 sách bài tập Toán lớp 6 Tập 1:
Viết các số nguyên biểu thị độ cao so với mực nước biển trong mỗi tình huống sau:
a) Máy bay ở độ cao 9 500 m.
b) Rặng san hô ở độ sâu 20m.
c) Hai mẹ con cá voi mũi khoằm Cuvier đang bơi ở độ sâu 1 000m.
Lời giải:
a) Số nguyên biểu diễn cho độ cao của máy bay so với mực nước biển là: 9 500 m.
b) Số nguyên biểu diễn cho độ cao của rặng san hô so với mực nước biển là: - 20m.
c) Số nguyên biểu diễn cho độ cao của hai mẽ con cá voi mũi khoằm Cuvier so với mực nước biển là: 1 000m.
|
Bộ phận nhà giàn |
Độ cao |
|
Phần 3 chân đỡ |
Dưới mực nước biển 15 m |
|
Phần 2 chân đỡ |
Dưới mực nước biển 9 m |
|
Phần 1 chân đỡ |
Dưới mực nước biển 4 m |
|
Tầng 1 |
Trên mực nước biển 8 m |
|
Tầng 2 |
Trên mực nước biển 18 m |
|
Tầng 3 |
Trên mực nước biển 25 m |
Sử dụng số nguyên để biểu thị các độ cao đó (so với mực nước biển).
Lời giải:
Số nguyên biểu diễn độ cao của phần 3 chân đỡ là: - 15 m;
Số nguyên biểu diễn độ cao của phần 2 chân đỡ là: - 9 m;
Số nguyên biểu diễn độ cao của phần 2 chân đỡ là: - 4 m;
Số nguyên biểu diễn độ cao của tầng 1 là: 8 m;
Số nguyên biểu diễn độ cao của tầng 1 là: 18 m;
Số nguyên biểu diễn độ cao của tầng 1 là: 25 m;
Bài 13 trang 73 sách bài tập Toán lớp 6 Tập 1:
a) Các điểm A, B, C, D trên trục số ở Hình 2 biểu diễn những số nguyên nào?
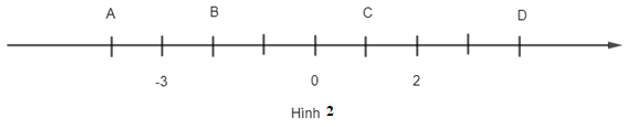
b) Hãy điền tên E, F, G, H, I lần lượt cho các điểm biểu diễn các số nguyên – 5; - 4; - 2; 3; 5 trên trục số ở Hình 3.
c) Ghi điểm gốc 0 vào trục số ở Hình 4.
Lời giải:
a) Quan sát trục số, ta thấy:
Điểm A nằm liền trước điểm – 3 nên điểm A biểu diễn cho số nguyên – 4;
Điểm B nằm liền sau điểm – 3 nên điểm B biểu diễn cho số nguyên – 2;
Điểm C nằm liền sau điểm 0 nên điểm C biểu diễn cho số nguyên 1;
Điểm D nằm sau điểm 2 và cách điểm 2 hai đơn vị nên điểm D biểu diễn cho số nguyên 4.
b) Sau khi điền các điểm E, F, G, H, I , ta được trục số sau:
c) Ta có điểm – 3 cách gốc tọa độ 0 ba đơn vị về bên trái hay điểm 0 cách điểm – 3 ba đơn vị về bên phải. Khi đó ta có hình vẽ biểu diễn điểm 0 như sau:
Bài 14 trang 74 sách bài tập Toán lớp 6 Tập 1:
Quan sát trục số ở hình 5 và trả lời các câu hỏi:
a) Điểm biểu diễn số 3 cách điểm 0 bao nhiêu đơn vị?
b) Số nguyên nào có điểm biểu diễn cách điểm gốc 0 một khoảng là 2 đơn vị?
c) Số nguyên âm nào có điểm biểu diễn cách điểm 2 một khoảng là 3 đơn vị?
d) Số nguyên dương nào có điểm biểu diễn cách điểm -1 một khoảng là 5 đơn vị?
Lời giải:
a) Trên trục số điểm biểu diễn số 3 cách điểm 0: 3 đơn vị.
b) Quan sát trên trục số, ta thấy có hai số nguyên là 2 và – 2 đều cách điểm 0 một khoảng 2 đơn vị.
c) Từ điểm 2 trên trục số ta lùi sang bên trái 3 đơn vị sẽ được điểm -1. Vậy số -1 là số nguyên âm biểu diễn cho điểm cách điểm 2 một khoảng 3 đơn vị.
d) Từ điểm – 1 trên trục số ta lùi sang bên phải 5 đơn vị sẽ được điểm 4. Vậy số 4 là số nguyên dương biểu diễn cho điểm cách điểm – 1 một khoảng là 5 đơn vị.
Bài 15 trang 74 sách bài tập Toán lớp 6 Tập 1: Vẽ một trục số nằm ngang, sau đó:
a) Chỉ ra các số nguyên có điểm biểu diễn cách điểm gốc 0 một đoạn là 4 đơn vị.
b) Nêu ra ba cặp số nguyên có điểm biểu diễn cách đều điểm 0.
Lời giải:
Ta có trục số sau:
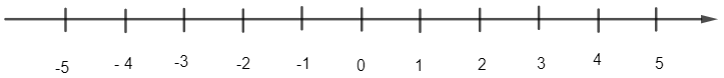
a) Quan sát trên trục số, ta thấy điểm - 4 cách gốc 0 một khoảng 4 đơn vị về bên trái và điểm 4 cách gốc 0 một khoảng 4 đơn vị về bên phải.
Vậy có hai số nguyên là 4 và -4 cùng cách điểm gốc 0 một đoạn là 4 đơn vị.
b) Ba cặp số nguyên có điểm biểu diễn cách đều điểm 0 là:
3 và – 3 cùng cách điểm gốc 0 một khoảng 3 đơn vị;
5 và – 5 cùng cách điểm gốc 0 một khoảng 5 đơn vị;
-1 và 1 cùng cách điểm gốc 0 một khoảng 1 đơn vị.
a) Có điểm biểu diễn nằm bên phải điểm gốc 0 và cách gốc 0 một khoảng là 3 đơn vị. Sau đó tìm số đối của các số nguyên đó.
b) Có điểm biểu diễn cách điểm 1 một khoảng 3 đơn vị. Sau đó, tìm số đối của các số nguyên đó.
Lời giải:
a) Có điểm biểu diễn nằm bên phải điểm gốc 0 và cách gốc 0 một khoảng là 3 đơn vị là 3.
Số đối của 3 là – 3.
b) Điểm 4 cách điểm 1 một khoảng 3 đơn vị về bên phải.
Điểm – 2 cách điểm 1 một khoảng 3 đơn vị về bên trái.
Số đối của 4 là – 4; số đối của - 2 là 2.
Lời giải:
+) Số đối của – 54 là 54;
+) Số đối của – 432 là 432;
+) Số đối của – 1 234 là 1 234;
+) Số đối của 767 là – 767;
+) Số đối của 8 765 là – 8 765;
+) Số đối của 100 000 là – 100 000.
Bài 18 trang 74 sách bài tập Toán lớp 6 Tập 1:
a) So sánh các cặp số sau: 52 và – 25; 0 và -17; - 315 và 314; 1 231 và 1 321.
b) Sắp xếp các số sau: 2; -21; 34; -541; - 1 276; 127; -32 156 theo thứ tự giảm dần.
Lời giải:
a) Trên trục số 52 nằm bên phải -25 nên ta có 52 > -25;
Trên trục số - 17 nằm bên trái 0 nên 0 > -17;
Trên trục số 314 nằm bên phải điểm – 315 nên 314 > - 315;
Trên trục số 1 231 nằm bên trái 1 321 nên 1 231 < 1 321.
b) Theo thứ tự giảm dần ta có dãy số sau: 127; 34; 2; -21; -541; - 1 276; -32 156.
Lý thuyết Tập hợp các số nguyên
I. Tập hợp các số nguyên
+ Số tự nhiên khác 0 còn được gọi là số nguyên dương.
+ Các số nguyên âm, số 0 và các số nguyên dương tạo thành tập hợp các số nguyên.
+ Tập hợp các số nguyên được kí hiệu là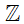 
.
Ví dụ:
+ Các số nguyên dương: 4, 6, 10 000, …
+ Tập hợp các số nguyên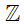 
= {…, – 2, – 1, 0, 1, 2, …}
Chú ý:
+ Số 0 không phải số nguyên âm, cũng không phải số nguyên dương.
+ Các số nguyên dương 1, 2, 3,... đều mang dấu “+" nên còn được viết là + 1, + 2, + 3,...
II. Biểu diễn số nguyên trên trục số
Ta có thể biểu diễn số nguyên trên trục số. Có hai loại trục số:
1. Trục số nằm ngang
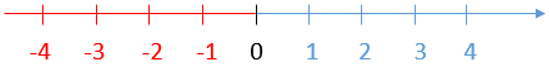
Trên trục số nằm ngang, điểm biểu diễn số nguyên âm nằm bên trái điểm 0, điểm biểu diễn số nguyên dương nằm bên phải điểm 0.
2. Trục số thẳng đứng
Trên trục số thẳng đứng, điểm biểu diễn số nguyên âm nằm phía dưới điểm 0, điểm biểu diễn số nguyên dương nằm phía trên điểm 0.
Chú ý: Khi nói “trục số” mà không nói gì thêm, ta hiểu là nói về trục số nằm ngang.
III. Số đối của một số nguyên
+ Trên trục số, hai số nguyên (phân biệt) có điểm biểu diễn nằm về hai phía của gốc 0 và cách đều gốc 0 được gọi là hai số đối nhau.
+ Số đối của 0 là 0.
Ví dụ:
– 4 và 4 là hai số đối nhau.
– 4 là số đối của 4 và 4 là số đối của – 4.
IV. So sánh các số nguyên
1. So sánh hai số nguyên
+ Trên trục số nằm ngang, nếu điểm a nằm bên trái điểm b thì số nguyên a nhỏ hơn số nguyên b.
+ Trên trục số thẳng đứng, nếu điểm a nằm phía dưới điểm b thì số nguyên a nhỏ hơn số nguyên b.
+ Nếu a nhỏ hơn b thì ta viết là a < b hoặc b > a.
Ví dụ:
Điểm – 10 nằm bến trái điểm – 5 nên – 10 < – 5
Điểm 2 nằm bên phải điểm 0 nên 2 > 0.
Chú ý:
+ Số nguyên dương luôn lớn hơn 0. Số nguyên âm luôn nhỏ hơn 0.
+ Nếu a < b và b < c thì a < c
Ví dụ: – 2 < 0 và 0 < 5 thì – 2 < 5.
2. Cách so sánh hai số nguyên
2.1 So sánh hai số nguyên khác dấu
Số nguyên âm luôn nhỏ hơn số nguyên dương.
Ví dụ: – 7 là số nguyên âm và 5 là số nguyên dương nên – 7 < 5.
2.2 So sánh hai số nguyên cùng dấu
+ So sánh hai số nguyên dương: Đã biết ở chương I.
+ So sánh hai số nguyên âm:
Để so sánh hai số nguyên âm, ta làm như sau:
Bước 1. Bỏ dấu “–” trước cả hai số âm
Bước 2. Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (trước khi bỏ dấu “–”) sẽ lớn hơn.
Ví dụ: So sánh – 216 và – 309.
Bỏ dấu “–” trước các số – 216 và – 309, ta được các số lần lượt là 216 và 309.
Do 216 < 309 nên – 216 > – 309.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
