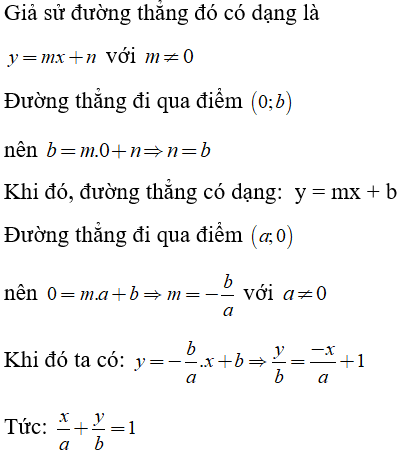Với tóm tắt lý thuyết Toán lớp 9 Hàm số bậc nhất hay, chi tiết cùng với bài tập chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 9.

Toán 9 Bài 2:Hàm số bậc nhất

A. Lý thuyết Hàm số bậc nhất

I. Định nghĩa 

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số cho trước và a ≠ 0

Chú ý: Khi b = 0 ta có hàm số y = ax (đã học ở lớp 7)

Ví dụ: Cho các hàm số

     y = 2x;     y = x + 1;     y = (1/2)x + 2;

    y = 3x + 1;      y = 4x - 1;      y = 2 - 3x;

Đây là các hàm số bậc nhất.

II. Tính chất

Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R. Có các tính chất như sau:

    + Đồng biến trên R khi a > 0

    + Nghịch biến trên R khi a < 0

Ví dụ 1: Cho các hàm số sau: y = 3x + 2, y = -x + 1, y = (1/2)x + 1; y = -√3x Hàm số nào đồng biến, hàm số nào nghịch biến ?

Hàm số đồng biến là: y = 3x + 2; y = (1/2)x + 1

Hàm số nghịch biến là: y = -x + 1; y = -√3x

Ví dụ 2: Xác định m để hàm số y = (m - 1)x + 2 đồng biến

Giải:

Hàm số đồng biến khi và chỉ khi m - 1 > 0 ⇒ m > 1

Vậy với m > 1 thì hàm số đã cho đồng biến

Ví dụ 3: Cho hàm số y = 2x² + 3. Hàm số này có phải hàm số bậc nhất không?

Giải:

Vì hàm số bậc nhất có dạng là y = ax + b nên hàm số đã cho y = 2x² + 3 không phải là hàm số bậc nhất

Ví dụ 4: Cho hàm số y = ax + 1. Biết đồ thị hàm số đi qua điểm A(1;2). Tìm giá trị của a?

Giải:

Đồ thị hàm số đi qua điểm A(1;2) nên ta có: 2 = a.1 + 1 ⇒ a = 1

Vậy a = 1 là giá trị cần tìm

B. Bài tập tự luận

Câu 1: Xác định đường thẳng đi qua hai điểm A và B biết A(-20; 0) và B(0; 1)

Lời giải

Câu 2: Chứng minh rằng nếu một đường thẳng không đi qua gốc tọa độ, cắt trục hoành tại điểm có hoành độ bằng a, cắt trục tung tại điểm có tung độ bằng b thì đường thẳng đó có phương trình là 

Lời giải