Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 2 Bài 2: NHàm số bậc nhất. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 2 Bài 2: Hàm số bậc nhất. Mời các bạn đón xem:
Bài tập Toán 9 Chương 2 Bài 2: Hàm số bậc nhất
A. Bài tập Hàm số bậc nhất
I. Bài tập trắc nghiệm
Câu 1: Chọn đáp án đúng nhất. Hàm số y = ax + b là hàm số bậc nhất khi:
A. a = 0
B. a < 0
C. a > 0
D. a ≠ 0
Hàm số bậc nhất là hàm số có dạng: y = ax + b (a ≠ 0)
Chọn đáp án D.
Câu 2: Chọn đáp án đúng nhất. Hàm số y = ax + b là hàm số đồng biến khi:
A. a = 0
B. a < 0
C. a > 0
D. a ≠ 0
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của thuộc R và có tính chất sau:
• Đồng biến trên R nếu a > 0
• Nghịch biến trên R nếu a < 0
Chọn đáp án C.
Câu 3: Hàm số nào dưới đây là hàm số bậc nhất:
Theo định nghĩa thì hàm số y = 2x + 1 là hàm số bậc nhất.
Chọn đáp án A.
Câu 4: Hàm số nào dưới đây không là hàm số bậc nhất?
Theo định nghĩa thì các hàm số 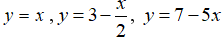
Hàm số 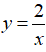
Chọn đáp án C.
Câu 5: Tìm để hàm số 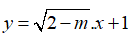
A. m < 2
B. m > 2
C. m = 2
D. m ≠ 2
Chọn đáp án A.
Câu 6: Cho hàm số y = (2m -4)x + 100 . Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất?
A. m ≠ 2
B. m ≠ -2
C. m > 2
D. m < -2
Hàm số bậc nhất là hàm số có dạng: y = ax + b (a ≠ 0)
Để hàm số đã cho là hàm số bậc nhất thì:
2m - 4 ≠ 0 ⇒ 2m ≠ 4 ⇒ m ≠ 2
Chọn đáp án A.
Câu 7: Cho hàm số bậc nhất y = ax + 4. Tìm hệ số a, biết rằng khi x = 1 thì y = 7 ?
A. -3
B. -10
C. 3
D. 10
Thay x = 1; y = 7 vào y = ax + 4, ta được:
7 = a.1 + 4
Suy ra: a = 3.
Chọn đáp án C.
Câu 8: Cho hàm số 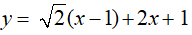
(1). Hàm số đã cho là hàm số bậc nhất
(2). Hàm số đã cho đồng biến trên R.
(3). Giá trị của hàm số tại x = 1 là 3.
Hỏi có bao nhiêu khẳng định đúng?
A. 0
B. 1
C. 2
D. 3
Ta có:
Chọn đáp án D.
Câu 9: Cho hàm số 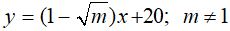
A. m < 1
B. 0 ≤ m < 1
C. m > 1
D. m ≥ 0
Chọn đáp án B.
Câu 10: Tìm điều kiện để hàm số 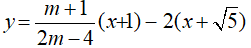
Chọn đáp án D.
Câu 11: Hàm số 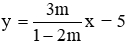
Hàm số 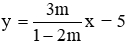
Đáp án cần chọn là: A
Câu 12: Hàm số nào sau đây là hàm số nghịch biến?
A. y = 2x – 1
B. y = − (1 – 3x)
C. y = − (2x – 1)
D. y = x
Hàm số y = 2x – 1 có a = 2 > 0 nên là hàm số đồng biến.
Hàm số y = − (1 – 3x) ⇔ y = 3x – 1 có a = 3 > 0 nên là hàm số đồng biến
Hàm số y = − (2x – 1) ⇔ y = −2x + 1 có a = −2 < 0 nên là hàm số nghịch biến
Hàm số y = x có a = 1 > 0 nên là hàm số đồng biến.
Đáp án cần chọn là: C
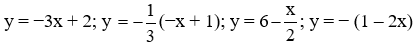 có bao nhiêu hàm số nghịch biến?
có bao nhiêu hàm số nghịch biến?A. 1
B. 3
C. 4
D. 2
Hàm số y = −3x + 2 có a = −3 < 0 nên là hàm số nghịch biến
Hàm số 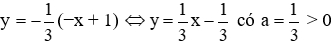
Hàm số 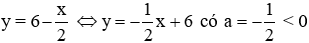
Hàm số y = − (1 – 2x) ⇔ y = 2x – 1 có a = 2 > 0 nên là hàm số đồng biến
Vậy có hai hàm số nghịch biến
Đáp án cần chọn là: D
Câu 14: Hàm số nào sau đây là hàm số bậc nhất và đồng biến?
+) Hàm số y = 2 (4 – x) + 5 = 8 – 2x + 5 ⇔ y = −2x + 13 có a = −2 < 0 nên là hàm số nghịch biến.
+) Hàm số y = √3 − (2x + 2) ⇔ y = √3 − 2x – 2 ⇔ y = −2x + √3 − 2 có a = −2 < 0 nên là hàm số nghịch biến.
+) Hàm số y = − (9 – x) ⇔ y = x – 9 có a = 1 > 0 nên là hàm số đồng biến
+) Hàm số y = x3 – x không là hàm số bậc nhất
Đáp án cần chọn là: D
Câu 15: Hàm số nào sau đây là hàm số đồng biến?
Hàm số 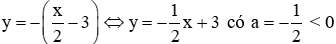
Hàm số 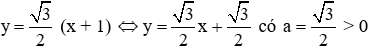
Hàm số y = − 5 – 3x ⇔ y = − 3x − 5 có a = −3 < 0 nên là hàm số nghịch biến
Hàm số y = − (9 + 3x) ⇔ y = −3x – 9 có a = − 3 < 0 nên là hàm số nghịch biến
Đáp án cần chọn là: B
II. Bài tập tự luận có lời giải
Câu 1: Cho các hàm số sau: y = 3x + 2, y = -x + 1, y = (1/2)x + 1; y = -√3x Hàm số nào đồng biến, hàm số nào nghịch biến ?
Lời giải:
Hàm số đồng biến là: y = 3x + 2; y = (1/2)x + 1
Hàm số nghịch biến là: y = -x + 1; y = -√3x
Câu 2: Xác định m để hàm số y = (m - 1)x + 2 đồng biến
Lời giải:
Hàm số đồng biến khi và chỉ khi m - 1 > 0 ⇒ m > 1
Vậy với m > 1 thì hàm số đã cho đồng biến
Câu 3: Cho hàm số y = 2x2 + 3. Hàm số này có phải hàm số bậc nhất không?
Lời giải:
Vì hàm số bậc nhất có dạng là y = ax + b nên hàm số đã cho y = 2x2 + 3 không phải là hàm số bậc nhất
Câu 4: Cho hàm số y = ax + 1. Biết đồ thị hàm số đi qua điểm A(1;2). Tìm giá trị của a?
Lời giải:
Đồ thị hàm số đi qua điểm A(1;2) nên ta có: 2 = a.1 + 1 ⇒ a = 1
Vậy a = 1 là giá trị cần tìm
III. Bài tập vận dụng
Câu 1: Xác định đường thẳng đi qua hai điểm A và B biết A(-20; 0) và B(0; 1)
Câu 2: Chứng minh rằng nếu một đường thẳng không đi qua gốc tọa độ, cắt trục hoành tại điểm có hoành độ bằng a, cắt trục tung tại điểm có tung độ bằng b thì đường thẳng đó có phương trình là
B. Lý thuyết Hàm số bậc nhất
1.Đồ thị hàm số y = ax + b (a ≠ 0)
Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:
- Cắt trục tung tại điểm có tung độ bằng b.
- Song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0
Chú ý. Đồ thị hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.
Ví dụ 1. Gọi A là giao điểm của hai đường thẳng y = x − 1 và y = 3x + 1, tìm tọa độ của điểm A?
Lời giải:
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
x − 1 = 3x + 1
3x − x = − 1 − 1
2x = − 2
x = − 1.
Với x = − 1 thì y = − 1 − 1 = − 2. Khi đó, A(− 1; − 2).
Vậy tọa độ giao điểm A(− 1; − 2).
2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)
• Khi b = 0 thì y = ax. Đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).
• Xét trường hợp y = ax + b với a ≠ 0 và b ≠ 0.
Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.
Cho y = 0 thì , ta được điểm thuộc trục hoành Ox.
Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0).
Chú ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.
Ví dụ 2. Vẽ đồ thị hàm số y = 2x – 1.
Bước 1: Cho x = 0 thì y = −1, ta được điểm A(0; −1) ∈ Oy.
Cho y = 1 thì 2x – 1 = 1 x = 1, ta được điểm B(1; 1)
Bước 2: Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = 2x – 1.
Ta có đồ thị hàm số:




