Với tóm tắt lý thuyết Toán lớp 9 Căn bậc hai hay, chi tiết cùng với bài tập chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 9.

Toán 9 Bài 1: Căn bậc hai

A. Lý thuyết Căn bậc hai

I. Căn bậc hai

1. Khái niệm

Căn bậc hai của một số a không âm là số x sao cho x² = a

2. Tính chất

- Số âm không có căn bậc hai

- Số 0 có đúng một căn bậc hai đó chính là số 0, ta viết √0 = 0

- Số dương a có đúng hai căn bậc hai là hai số đối nhau; số dương ký hiệu là √a, số âm ký hiệu là -√a

3. Ví dụ cụ thể

- Số 25 có hai căn bậc hai là 5 và -5.

- Số 7 có hai căn bậc hai là √7 và -√7

- Số -1 không có căn bậc hai.

II. Căn bậc hai số học

1. Định nghĩa

- Với số dương a, số √a được gọi là căn bậc hai số học của a.

- Số 0 cũng được gọi là căn bậc hai số học của 0.

- Ta viết x = √a

- Ví dụ:

Căn bậc hai số học của 4 là √4 (= 2).

Căn bậc hai số học của 5 là √5 (≈ = 2,236067977...)

Ví dụ 1: Tìm căn bậc hai số học của các số sau đây: 121; 144; 361; 400

Giải:

2. Phép khai phương

- Phép khai phương là phép toán tìm căn bậc hai số học của số không âm (gọi tắt là khai phương).

- Khi biết một căn bậc hai số học của một số, ta dễ dàng xác định được các căn bậc hai của nó.

- Ví dụ:

Căn bậc hai số học của 49 là 7 nên 49 có hai căn bậc hai là 7 và -7.

Căn bậc hai số học cuả 100 là 10 nên 100 có hai căn bậc hai là 10 và -10

Căn bậc hai số học của 144 là 12 nên 144 có hai căn bậc hai là 12 và -12

3. Một số kết quả cần nhớ

- Với a ≥ 0 thì a = (√a)².

- Với a ≥ 0, nếu x ≥ 0 và x² = a thì x = √a.

- Với a ≥ 0 và x² = a thì x = ±√a.

III. So sánh các căn bậc hai số học

1. Định lý

Với hai số a và b không âm, ta có: a > b ⇔ √a > √b

2. Ví dụ cụ thể: So sánh

- 1 với √2.

Hướng dẫn:

Ta có 1 < 2 ⇒ √1 < √2 ⇒ 1 < √2.

- 3 với √7.

Hướng dẫn:

Ta có 9 > 7 ⇒ √9 > √7 ⇒ 3 > √7.

Ví dụ 1: So sánh:

a) 2 và √3              b) 7 và √51

Giải:

a) Ta có: 2 = √4 mà 4 > 3 nên √4 > √3 tức 2 > √3

b) Ta có: 7 = √49 mà 49 < 51 nên √49 < √51 tức 7 < √51

B. Bài tập tự luận

Câu 1: Tìm căn bậc hai của các số sau: 9; 9/25; 1,21; -144.

- Vì 9 > 0 nên 9 có hai căn bậc hai là 3 và -3, vì 3² = 9 và (-3)² = 9.

- Vì 9/25 > 0 nên 9/25 có hai căn bậc hai là 3/5 và -3/5, vì (3/5)² = 9/25 và (-3/5)² = 9/25.

- Vì 1,21 > 0 nên 1,21 có hai căn bậc hai là 1,1 và -1,1, vì 1,1² = 1,21 và (-1,1)² = 1,21.

- Theo tính chất, số âm không tồn tại căn bậc hai nên -144 không có căn bậc hai.

Câu 2: Giải các phương trình sau:

a) x² = 5.     b) x² + 2 = 0     c) (x - 2)² = 7

- Giải phương trình x² = 5. Do 5 > 0 nên 5 có hai căn bậc hai là √5 và -√5

     Suy ra 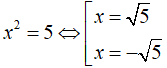. Vậy S = {√5; -√5}

- Giải phương trình x² = -2. Vì -2 < 0 nên -2 không có căn bậc hai. Suy ra phương trình vô nghiệm. Vậy S = ∅

- Giải phương trình (x - 2)² = 7. Do 7 > 0 nên 7 có hai căn bậc hai là √7 và -√7.

Suy ra

Vậy S = {2 - √7; 2 + √7}

Trình bày gọn:

Câu 3: So sánh các số sau:

a) 6 và √35     b) 3 và √5     c) √7 với √5.

a) Ta có: 36 > 35 ⇒ √36 > √35 ⇒ 6 > √35

b) Ta có: 9 > 5 ⇒ √9 > √5 ⇒ 3 > √5

c) Ta có: 7 > 5 ⇒ √7 > √5