Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 8 Bài 6: Cộng, trừ phân thức sách Chân trời sáng tạo. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 8.
Trắc nghiệm Toán 8 Bài 6: Cộng, trừ phân thức
Câu 1. Với x = 2023 hãy tính giá trị của biểu thức: .
A.
B.
C.
D.
Đáp án đúng là: B
Với x = 2023, ta có:
.
Câu 2. Tìm x, biết :
A. x = 0
B.
C. x = 1
D.
Đáp án đúng là: D
Ta có
Mà nên
Vậy .
Câu 3. Rút gọn biểu thức sau: .
A.
B.
C.
D.
Đáp án đúng là: D
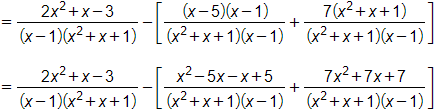
Câu 4. Giá trị của biểu thức với là
A.
B.
C.
D.
Đáp án đúng là: D
.
Với , ta có:
.
Câu 5. Tính tổng sau: .
A. A = 1
B. A = 0
C.
D.
Đáp án đúng là: D
Câu 6. Chọn khẳng định đúng.
A.
B.
C.
D.
Đáp án đúng là: C
Quy đồng mẫu thứcvà , ta có:
.
Do đó .
Câu 7. Phân thức đối của phân thức là
A.
B.
C.
D.
Đáp án đúng là: B
Phân thức đối của phân thức là .
Câu 8. Thực hiện phép tính sau:
A. x + 2
B. 2x
C. x
D. x – 2
Đáp án đúng là: D
Câu 9. Tìm phân thức A thỏa mãn: .
A.
B.
C.
D.
Đáp án đúng là: B
Suy ra
.
Câu 10. Cho . Phân thức thu gọn của A có tử thức là:
A.
B.
C.
D.
Đáp án đúng là: C
.
Câu 11. Cho 3y – x = 63. Tính giá trị của biểu thức .
A. 1
B. 2
C. 3
D. 4
Đáp án đúng là: D
Ta có 3y – x = 6 nên x = 3y – 63
Thay x = 3y – 6 vào, ta được:
Câu 12. Kết luận nào sau đây là đúng khi nói về giá trị của biểu thức tại ?
A. 0 < A < 1
B. A = 0
C. A = 1
D.
Đáp án đúng là: A
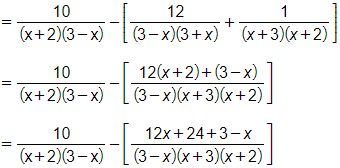
Tại ta có
Vậy 0 < A < 1.
Câu 13. Tìm giá trị nguyên của x để biểu thức có giá trị là một số nguyên.
A. x = 0
B. x = 1
C.
D. 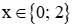
Đáp án đúng là: D
Để hay thì x – 1 ∈ Ư(1) = {−1; 1}.
Ta có bảng sau:
|
x – 1
|
−1
|
1
|
|
x
|
0 (TM)
|
2 (TM)
|
Câu 14. Có bao nhiêu giá trị của x để biểu thức có giá trị là một số nguyên?
A. 1
B. 2
C. 3
D. 4
Đáp án đúng là: C
Điều kiện: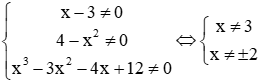
Để 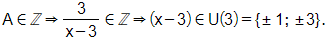
.
Ta có bảng sau:
|
x – 3
|
–3
|
–1
|
1
|
3
|
|
x
|
0 (TM)
|
2 (KTM)
|
4 (TM)
|
6 (TM)
|
Vậy có 3 giá trị của x để biểu thức A có giá trị là một số nguyên.
Câu 15. Rút gọn biểu thức 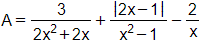
biết .
A.
B.
D.
Đáp án đúng là: A
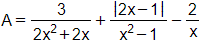
Câu 16. Cho. Số thích hợp điền vào chỗ trống là
A. 16
B. 8
C. 4
D. 20