Với giải Bài 59 trang 118 SBT Toán lớp 11 Cánh diều chi tiết trong Bài tập cuối chương 4 trang 117 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài tập cuối chương 4 trang 117
Bài 59 trang 118 SBT Toán 11: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, AD; P, Q lần lượt thuộc các cạnh CD, BC (P, Q không trùng các đỉnh B, C, D). Chứng minh rằng nếu M, N, P, Q cùng thuộc một mặt phẳng thì PQ song song với BD.
Lời giải:
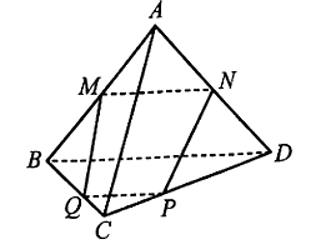
Giả sử M, N, P, Q cùng thuộc một mặt phẳng.
Vì M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của tam giác ABD, do đó MN // BD.
Do P ∈ CD nên P ∈ (BCD) và Q ∈ BC nên Q ∈ (BCD), suy ra PQ ⊂ (BCD).
Mà PQ ⊂ (MNPQ) nên PQ là giao tuyến của hai mặt phẳng (BCD) và (MNPQ).
Hai mặt phẳng (MNPQ) và (BCD) có MN // BD và PQ là giao tuyến.
Suy ra PQ // BD.
Xem thêm lời giải sách bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 57 trang 118 SBT Toán 11: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh SD...
Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác:
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 5: Hình lăng trụ và hình hộp
Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
