Với lời giải SBT Toán 7 trang 25 Tập 1 chi tiết trong Bài tập cuối chương 1 sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài tập cuối chương 1
Bài 45 trang 25 SBT Toán 7 Tập 1: Trong Hình 9, điểm nào biểu diễn số hữu tỉ trên trục số?

A. Điểm M.
B. Điểm N.
C. Điểm P.
D. Điểm Q.
Lời giải:
Ta thấy nên điểm biểu diễn số hữu tỉ nằm bên phải số 1 trên trục số.
Trên trục số Hình 9 chỉ có điểm Q nằm bên phải số 1 nên điểm Q biểu diễn số hữu tỉ .
Chọn đáp án D.
Bài 46 trang 25 SBT Toán 7 Tập 1:
Kết quả phép tính là:
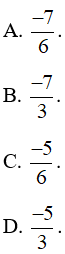
Lời giải:
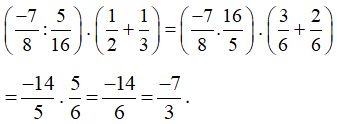
Chọn đáp án B.
Bài 47 trang 25 SBT Toán 7 Tập 1: Giá trị của x trong đẳng thức (3x – 2)2 = 2 . 23 là:
A. 2.
B. và 2.
C. và 2.
D. và 2.
Lời giải:
(3x – 2)2 = 2 . 23
(3x – 2)2 = 16
(3x – 2)2 = 42
Trường hợp 1: 3x – 2 = 4
3x = 4 + 2
3x = 6
x = 2.
Trường hợp 1: 3x – 2 = –4
3x – 2 = –4
3x = –4 + 2
3x = –2
.
Vậy .
Chọn đáp án C.
Bài 48 trang 25 SBT Toán 7 Tập 1:
Trong các phân số , phân số viết được dưới dạng số thập phân vô hạn tuần hoàn là:
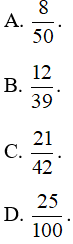
Lời giải:
Ta có:
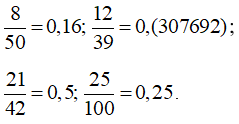
Trong các phân số , phân số viết được dưới dạng số thập phân vô hạn tuần hoàn.
Chọn đáp án B.
Bài 49 trang 25 SBT Toán 7 Tập 1: Biểu diễn các số hữu tỉ lần lượt bằng các điểm A, B, C trên trục số ở Hình 10.

Lời giải:
Ta có: .
Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng đơn vị cũ).
Đi theo ngược chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 2 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ hay .
Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 1 đơn vị mới đến điểm B. Điểm B biểu diễn số hữu tỉ .
Điểm C biểu diễn số hữu tỉ 1.
Ta biểu diễn các điểm A, B, C trên trục số như sau:
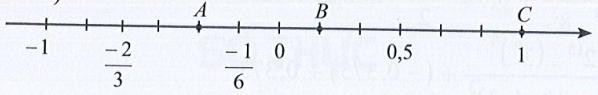
Bài 50 trang 25 SBT Toán 7 Tập 1:
a) Sắp xếp các số sau theo thứ tự tăng dần: .
b) Sắp xếp các số sau theo thứ tự giảm dần: .
Lời giải:
a) ∙ Nhóm các số hữu tỉ âm: .
Ta có .
Vì −3,7 < −2,1(6) < −0,2 nên .
∙ Nhóm các số hữu tỉ dương: .
Ta thấy: .
Ta có ; .
Vì 33 < 42 nên .
Do đó .
Từ đó suy ra .
Vậy các số được sắp xếp theo thứ tự tăng dần là:
b) ∙ Nhóm các số hữu tỉ âm: .
Ta có .
Vì nên suy ra .
∙ Nhóm các số hữu tỉ dương: .
Ta có: .
Vì 2,45 > 2,2 > 0,3541(5) nên .
Do đó .
Vậy các số được sắp xếp theo thứ tự giảm dần: .
Bài 51 trang 25 SBT Toán 7 Tập 1: Tính giá trị của mỗi biểu thức sau:
a) ;
b) ;
c) ;
d) (0,1)21 : (−0,01)10.
Lời giải:
a) ;
b)
= −10 + 0,2 = −9,8;
c)
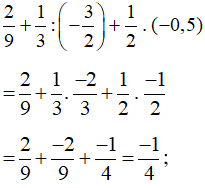
d) (0,1)21 : (−0,01)10
= (0,1)21 : (0,01)10
= (0,1)21 : (0,1)20 = 0,1.
Xem thêm các bài giải sách bài tập Toán 7 Cánh diều hay, chi tiết khác:
Giải SBT Toán 7 trang 26 Tập 1