Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Hàm số, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Hàm số. Mời các bạn đón xem:

Bài tập Toán 8 Hàm số

A. Bài tập Hàm số

Bài 1. Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau:

Đại lượng y có phải là hàm số của đại lượng x không?

Hướng dẫn giải

Đại lượng y là hàm số của đại lượng x vì mỗi giá trị của x chỉ xác định đúng một giá trị của y.

Bài 2. Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau:

Đại lượng y có phải là hàm số của đại lượng x không?

Hướng dẫn giải

Đại lượng y không là hàm số của đại lượng x vì với giá trị x = 3 thì y nhận hai giá trị là 2 và 5.

Bài 3. Cho hàm số y = f(x) = 3x. Tính f(1); f(−2); $f\left(\frac{1}{3}\right)$ .

Hướng dẫn giải

f(1) = 3.1 = 3; f(−2) = 3.(−2) = −6 ; $f\left(\frac{1}{3}\right)=3.\frac{1}{3}=1$ .

Bài 4. Thời gian t (giờ) của một vật chuyển động đều trên quãng đường 20 km tỉ lệ nghịch với tốc độ v (km/h) của nó theo công thức $t=\frac{20}{v}$ . Đại lượng t có phải là hàm số của đại lượng v hay không? Nếu có, tính thời gian chuyển động của vật đó biết tốc độ của vật là 40 km/h?

Hướng dẫn giải

Đại lượng t là hàm số của đại lượng v vì mỗi giá trị của v ta nhận được chỉ một giá trị của t.

Với v = 40 km/h thì $t=\frac{20}{40}=\frac{1}{2}$  (giờ).

Bài 5. Tìm tập xác định của các hàm số sau:

Hướng dẫn giải

a) ĐKXĐ:

⇒ TXĐ: D = [1; +∞)\{2}.

b) ĐKXĐ:

⇒ TXĐ: D = (1; +∞).

c) ĐKXĐ: x² + x + 1 ≠ 0 ⇔ (x + 1/2)² + 3/4 ≠ 0 (đúng ∀ x)

⇒ TXĐ: D = R.

d) ĐKXĐ:

⇒ TXĐ: D = [-1;+∞)\{3}

⇒ TXĐ: D = R\{2}

Bài 6. Tìm giá trị của tham số m để:

a) Hàm số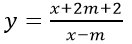xác định trên (-1; 0)

b) Hàm số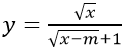có tập xác định là [0; +∞)

Hướng dẫn giải

a) ĐKXĐ: x ≠ m

Hàm số xác định trên (-1; 0) ⇔ m ∉ (-1; 0)

⇔

Vậy với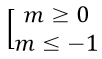thì hàm số xác định trên (-1; 0)

b) ĐKXĐ:

Nếu m > 0 thì (*) ⇔ x ≥ m ⇒ D = [m; +∞) nên m > 0 không thỏa mãn

Nếu m ≤ 0 thì (*) ⇔ x ≥ 0 ⇒ D = [0; +∞)

Vậy m ≤ 0 là giá trị cần tìm.

Bài 7. Tìm giá trị của tham số m để:

a) Hàm số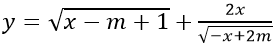xác định trên (-1; 3)

b) Hàm số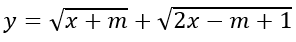xác định trên (0;+∞)

Hướng dẫn giải

a) Hàm số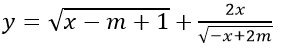xác định trên (-1; 3)

ĐKXĐ:

Với m ≤ -1 thì (*) vô nghiệm.

Với m > -1 thì (*) ⇔ m - 1 ≤ x < 2m

Vậy không tồn tại m thỏa mãn yêu cầu đề bài.

b) Hàm số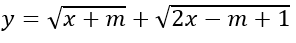xác định trên (0;+∞)

ĐKXĐ:

Ta có: (m - 1)/2 > -m ⇔ m > 1/3

Với m > 1/3 thì (2) ⇔ x ≥ (m - 1)/2

⇒ D = [(m - 1)/2; +∞)

Khi đó hàm số xác định trên (0; +∞) khi (m - 1)/2 ≤ 0 ⇔ m ≤ 1

⇒ 1/3 < m ≤ 1

Với m ≤ 1/3 thì (2) ⇔ x ≥ -m ⇒ D = [-m; +∞)

Khi đó hàm số xác định trên (0; +∞) khi -m ≤ 0 ⇔ m ≥ 0

⇒ 0 ≤ m ≤ 1/3

Vậy các giá trị m cần tìm là 0 ≤ m ≤ 1.

B. Lý thuyết Hàm số

1. Định nghĩa

Nếu đại lượng y phụ thuộc vào đại lượng x (x thay đổi) sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.

Ví dụ:

+ Một hình lập phương có độ dài cạnh là x (cm). Thể tích của hình lập phương V = x³ (cm³). Khi đó, ta nói V là hàm số của x vì mỗi giá trị của x ta chỉ xác định đúng một giá trị của V.

+ Cho bảng giá trị sau:

Khi đó đại lượng y là hàm số của đại lượng x vì mỗi giá trị của x chỉ xác định đúng một giá trị của y.

Chú ý:

+ Khi x thay đổi mà y luôn nhận một giá trị thì y được gọi là hàm hằng.

+ Hàm số có thể cho bằng công thức, bằng bảng.

+ Khi y là hàm số của x, ta có thể viết y = f(x), y = g(x). …

2. Giá trị của hàm số

Cho hàm số y = f(x) xác định tại x = a. Giá trị tương ứng của hàm số f(x) khi x = a được gọi là giá trị của hàm số y = f(x) tại x = a, kí hiệu là f(a).

Ví dụ:

+ Cho hàm số f(x) = x + 5

f(−2) = (−2) + 5 = 3 là giá trị của hàm số f(x) = x + 5 tại x = −2;

f(0) = 0 + 5 = 5 là giá trị của hàm số số f(x) = x + 5 tại x = 0.

+ Cho bảng giá trị sau

Nhìn vào bảng, ta thấy 3 là giá trị của hàm số y = f(x) = −2x + 1 tại x = −1 hay f(−1) = 3. Tương tự, f(1) = −1.