Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Phép cộng, phép trừ phân thức đại số, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Phép cộng, phép trừ phân thức đại số. Mời các bạn đón xem:

Bài tập Toán 8 Phép cộng, phép trừ phân thức đại số

A. Bài tập Phép cộng, phép trừ phân thức đại số

Bài 1.Thực hiện các phép cộng, trừ phân thức sau:

a) $\frac{2\text{x}+1}{x+y}+\frac{2y+1}{y+x}$;

b) $\frac{{\left(x-xy\right)}^2}{x^{2}y}-\frac{{\left(x+xy\right)}^2}{x^{2}y}$.

c) $\frac{3\text{x}+5}{x-2y}+\frac{x+1}{2\text{x}+y}$;

d) $\frac{1}{a+1}-\frac{1}{a^2+2\text{a}+1}$.

e) $\frac{5\text{x}-1}{x-5}+\frac{2\text{x}+3}{5-x}-\frac{x}{x-5}$;

f) $\text{x}+y+\frac{xy}{x+y}$.

Hướng dẫn giải

a) $\frac{2\text{x}+1}{x+y}+\frac{2y+1}{y+x}=\frac{2\text{x}+1}{x+y}+\frac{2y+1}{x+y}=\frac{2\text{x}+1+2y+1}{x+y}=\frac{2\text{x}+2y+2}{x+y}$.

Bài 2.Hai ô tô cùng đi từ thành phố A đến thành phố B cách nhau 300 km, biết vận tốc ô tô thứ nhất là x (km/h), vận tốc ô tô thứ nhất là y (km/h) (x > y). Nếu xuất phát cùng lúc thì ô tô nào đến trước và đến trước bao nhiêu giờ?

Hướng dẫn giải

Thời gian ô tô thứ nhất đi từ A đến B là $\frac{300}{x}$ (giờ)

Thời gian ô tô thứ hai đi từ A đến B là $\frac{300}{y}$ (giờ)

Vì x > y nên $\frac{300}{x}<\frac{300}{y}$

Suy ra ô tô thứ nhất sẽ đến B trước ô tô thứ hai.

Thời gian ô tô thứ nhất đến trước ô tô thứ hai là:

Vậy ô tô thứ nhất đến trước ô tô thứ hai và đến trước 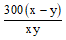 giờ.

Bài 3. Thực hiện phép tính:

a) $\frac{3x+2}{2}+\frac{2x-1}{2}$;

b) $\frac{3x-2y}{x-y}+\frac{x+2y}{y-x}$;

c) $\frac{2x+1}{x^2-4}+\frac{x-1}{x-2}$.

Hướng dẫn giải

a) $\frac{3x+2}{2}+\frac{2x-1}{2}=\frac{\left(3x+2\right)+\left(2x-1\right)}{2}$

$=\frac{3x+2+2x-1}{2}=\frac{5x+1}{2}$.

b) $\frac{3x-2y}{x-y}+\frac{x+2y}{y-x}=\frac{3x-2y}{x-y}+\left(-\frac{x+2y}{x-y}\right)$

$=\frac{3x-2y-x-2y}{x-y}=\frac{2x-4y}{x-y}$.

c) $\frac{2x+1}{x^2-4}+\frac{x-1}{x-2}$

$\begin{array}{l}=\frac{2x+1}{\left(x-2\right)\left(x+2\right)}+\frac{\left(x-1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\\ \end{array}$

$=\frac{2x+1}{\left(x-2\right)\left(x+2\right)}+\frac{x^2+2x-x-2}{\left(x-2\right)\left(x+2\right)}$

$=\frac{2x-1+x^2+2x-x-2}{\left(x-2\right)\left(x+2\right)}$

$=\frac{x^2+3x-3}{\left(x-2\right)\left(x+2\right)}$.

Bài 4. Thực hiện phép tính:

a) $\frac{1}{x-2}-\frac{1}{x+1}$;

b) $\frac{12}{x^2-9}-\frac{2}{x-3}$;

c) $\frac{1}{x-5x^2}-\frac{25x-15}{25x^2-1}$.

Hướng dẫn giải

a) $\frac{1}{x-2}-\frac{1}{x+1}=\frac{1\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}-\frac{1\left(x-2\right)}{\left(x+1\right)\left(x-2\right)}$

$=\frac{x+1-x+2}{\left(x+1\right)\left(x-2\right)}=\frac{3}{\left(x+1\right)\left(x-2\right)}$.

b) $\frac{12}{x^2-9}-\frac{2}{x-3}$ 

$=\frac{12}{\left(x-3\right)\left(x+3\right)}-\frac{2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}$

$=\frac{12-2x-6}{\left(x-3\right)\left(x+3\right)}$$=\frac{-2x+6}{\left(x-3\right)\left(x+3\right)}$

$=\frac{-2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}$$=\frac{-2}{x+3}$.

c) $\frac{1}{x-5x^2}-\frac{25x-15}{25x^2-1}$

$=\frac{1}{x\left(1-5x\right)}-\left[-\frac{25x-15}{\left(1-5x\right)\left(1+5x\right)}\right]$

$=\frac{1\left(1+5x\right)}{x\left(1-5x\right)\left(1+5x\right)}+\frac{\left(25x-15\right)x}{x\left(1-5x\right)\left(1+5x\right)}$

$=\frac{1+5x+25x-15}{x\left(1-5x\right)\left(1+5x\right)}=\frac{30x-14}{x\left(1-5x\right)\left(1+5x\right)}$.

Bài 5. Sử dụng quy tắc đổi dấu thực hiện phép tính sau theo cách hợp lí:

$\frac{4x^2-3x+17}{x^3-1}+\frac{2x-1}{x^2+x+1}+\frac{6}{1-x}$.

Hướng dẫn giải

$\frac{4x^2-3x+17}{x^3-1}+\frac{2x-1}{x^2+x+1}+\frac{6}{1-x}$

$=\frac{4x^2-3x+17}{\left(x-1\right)\left(x^2+x+1\right)}+\frac{2x-1}{x^2+x+1}-\frac{6}{x-1}$

$=\frac{4x^2-3x+17}{\left(x-1\right)\left(x^2+x+1\right)}+\frac{\left(2x-1\right)\left(x-1\right)}{\left(x^2+x+1\right)\left(x-1\right)}-\frac{6\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}$

$=\frac{4x^2-3x+17+2x^2-2x-x+1-6x^2-6x-6}{\left(x-1\right)\left(x^2+x+1\right)}$

$=\frac{-12x+12}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{-12\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}$

$=\frac{-12}{x^2+x+1}$.

B. Lý thuyết Phép cộng, phép trừ phân thức đại số

1. Phép cộng các phân thức đại số

1.1. Cộng hai phân thức cùng mẫu

Muốn cộng hai phân thức cùng mẫu, ta cộng các tử thức và giữ nguyên mẫu thức:

AM+BM=A+BM.

Ví dụ: x+3xy+y−3xy=(x+3)+(y−3)xy=x+3+y−3xy=x+yxy.

Chú ý: Kết quả của phép cộng hai phân thức được gọi là tổng. Ta thường viết tổng này dưới dạng rút gọn.

1.2. Cộng hai phân thức có mẫu thức khác nhau

Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.

Ví dụ:

2−xxy+x+3y+1=2−xx(y+1)+3y+1

=2−xx(y+1)+3xx(y+1)=2−x+3xx(y+1)=2+2xx(y+1).

1.3. Tính chất của phép cộng phân thức

Giống như phép cộng phân số, phép cộng phân thức cũng có các tính chất sau: giao hoán, kết hợp, cộng với 0.

Ví dụ:

P=2xx2+6x+9+x+1x+3+3−xx2+6x+9

=(2xx2+6x+9+3−xx2+6x+9)+x+1x+3

=2x+3−xx2+6x+9+x+1x+3

=x+3(x+3)2+x+1x+3

=1x+3+x+1x+3

=x+2x+3.

2. Phép trừ các phân thức đại số

2.1. Quy tắc trừ hai phân thức

- Muốn trừ hai phân thức cùng mẫu, ta trừ tử của hân thức bị trù cho tử của phân thức trừ và giữ nguyên mẫu:

AM−BM=A−BM.

- Muốn trừ hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi trừ các phân thức có cùng mẫu vừa tìm được.

Ví dụ:

• 3x+yx+y−2x−2yx+y=(3x+y)−(2x−2y)x+y

=3x+y−2x+2yx+y=x+3yx+y.

• 2−xxy+x−3y+1=2−xx(y+1)−3y+1

=2−xx(y+1)−3xx(y+1)=2−x−3xx(y+1)=2−4xx(y+1).

Chú ý: Kết quả của phép trừ hai phân thức được gọi là hiệu. Ta thường viết hiệu này dưới dạng rút gọn.

2.2. Phân thức đối

- Phân thức đối của phân thức AB kí hiệu là -AB. Ta có AB+(−AB)=0.

- Ta có: − AB=− AB=A− B.

- Phân thức đối của phân -AB là AB, tức là −(−AB)=AB.

- Muốn trừ phân thức AB cho phân thức CD, ta có thể cộng AB với phân thức đối của phân thức CD, tức là AB−CD=AB+(−CD).

Ví dụ:

Phân thức đối của phân thức 2xx+y là −2xx+y.

x−3yx−y−2yy−x=x−3yx−y+(−2yy−x)

=x−3yx−y+2yx−y=x−3y+2yx−y=x−yx−y=1.

Video bài giảng Toán 8 Bài 2: Phép cộng, phép trừ phân thức đại số - Cánh diều