Tailieumoi sưu tầm và biên soạn chuyên đề Quy đồng mẫu số các phân số lớp 4 gồm đầy đủ lý thuyết và 18 bài tập chọn lọc từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, biết cách làm bài tập môn Toán lớp 4.
Chuyên đề Quy đồng mẫu số các phân số lớp 4
I/ Lý thuyết
Khi quy đồng mẫu số hai phân số có thể làm như sau:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
II/ Các dạng bài tập
II.1/ Dạng 1: Quy đồng mẫu số các phân số có mẫu số không chia hết cho nhau
1. Phương pháp giải
Khi quy đồng mẫu số hai phân số có thể làm như sau:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Cho 2 phân số: và
Quy đồng mẫu số:
2. Ví dụ minh họa
Ví dụ 1: Quy đồng mẫu số hai phân số: và
Lời giải:
Vậy, quy đồng mẫu số 2 phân số và ta được 2 phân số và .
Ví dụ 2: Quy đồng mẫu số hai phân số: và
Lời giải:
Vậy, quy đồng mẫu số 2 phân số và ta được 2 phân số và .
II.2/ Dạng 2: Quy đồng mẫu số các phân số có mẫu số không chia hết cho nhau
1. Phương pháp giải
Cho 2 phân số và với b chia hết cho d:
Cách quy đồng mẫu số:
+ Bước 1: Lấy b : d = m
+ Bước 2: Nhân cả tử và mẫu của phân số với m, ta được: và
2. Ví dụ minh họa
Ví dụ 1: Quy đồng mẫu số các phân số: và
Lời giải:
Ta có: 9 : 3 = 3
Vậy, quy đồng mẫu số 2 phân số và ta được 2 phân số và .
Ví dụ 2: Quy đồng mẫu số các phân số: và
Lời giải:
Ta có: 8 : 4 = 2
Vậy, quy đồng mẫu số 2 phân số và ta được 2 phân số và .
III. Bài tập vận dụng
1. Bài tập có lời giải
Bài 1: Quy đồng mẫu số các phân số:
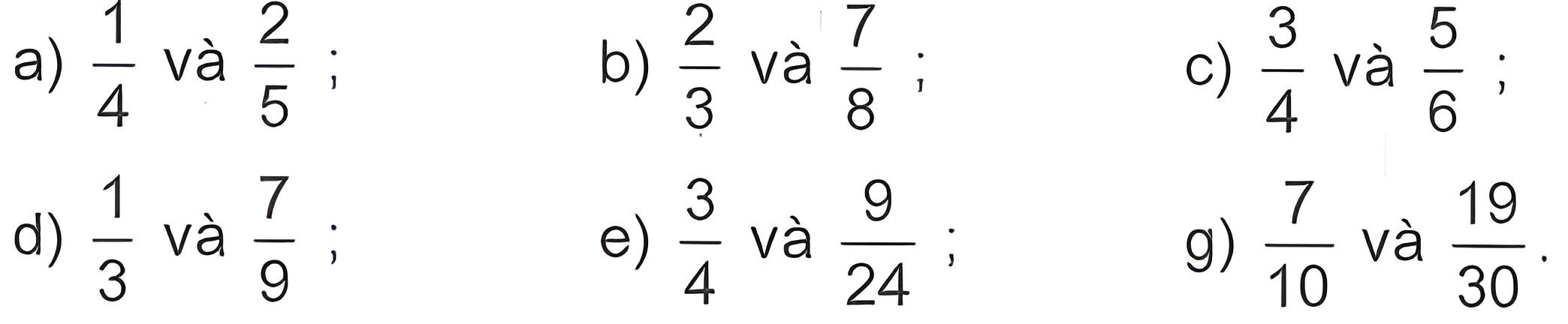
Lời giải:
Bài 2: Quy đồng mẫu số các phân số:

Lời giải:
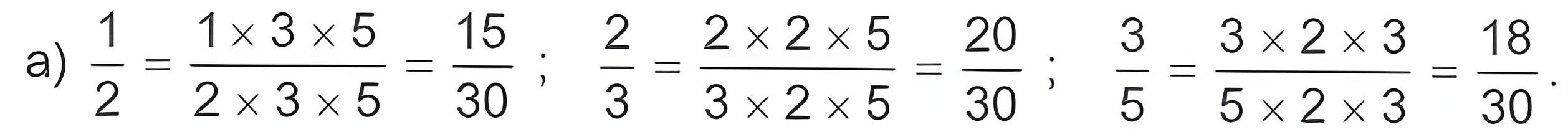
b) Chọn mẫu số chung là 24 (vì 24 chia hết cho 3, 4, 8). Sau khi quy đồng mẫu số ta được:
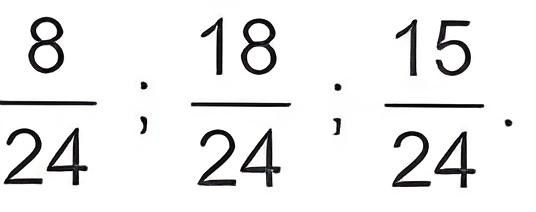
c) Chọn mẫu số chung là 30 (vì 30 chia hết cho 5, 6, 30) .Sau khi quy đồng mẫu số ta được:
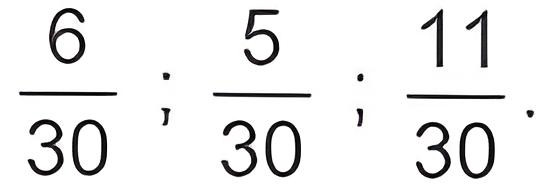
d) Chọn mẫu số chung là 12 (vì 12 chia hết cho 3, 4, 12) .Sau khi quy đồng mẫu số ta được:
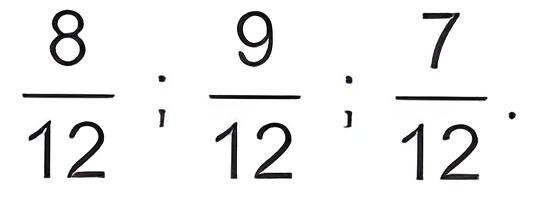
Bài 3: Quy đồng mẫu số các phân số sau:
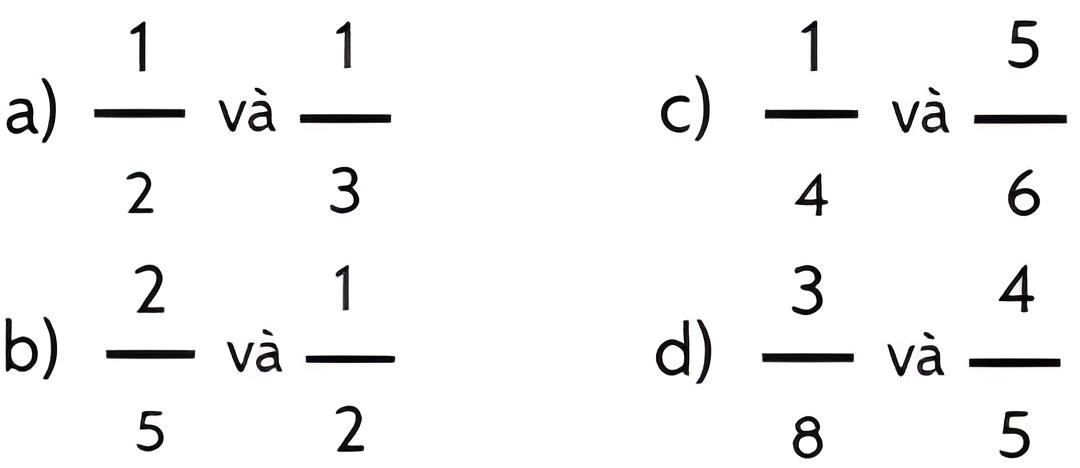
Lời giải:


Bài 4: Quy đồng mẫu số các phân số sau:
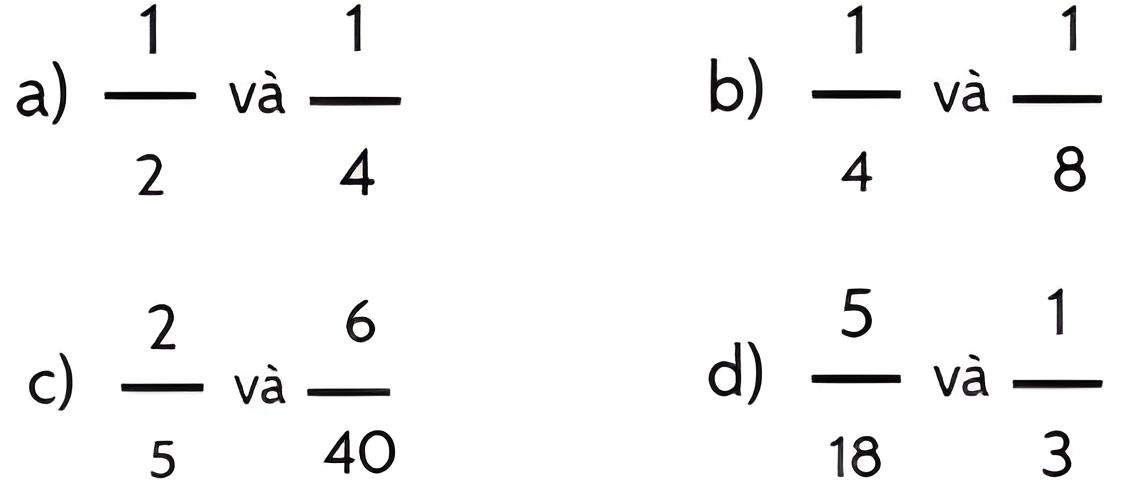
Lời giải:

Bài 5: Quy đồng mẫu số các phân số sau:
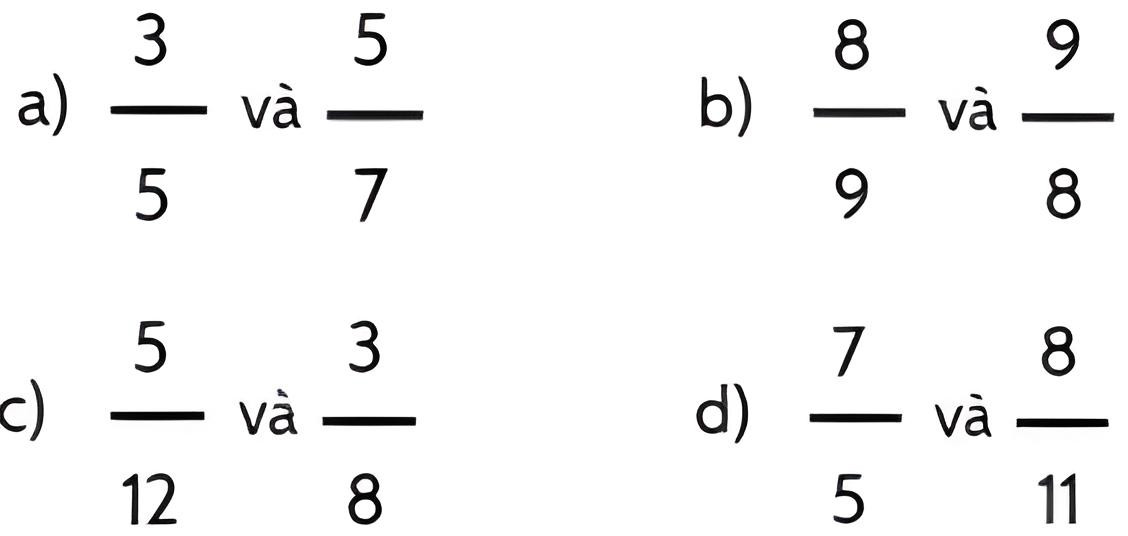
Lời giải:


Bài 6: Rút gọn phân số rồi quy đồng mẫu số các phân số sau :
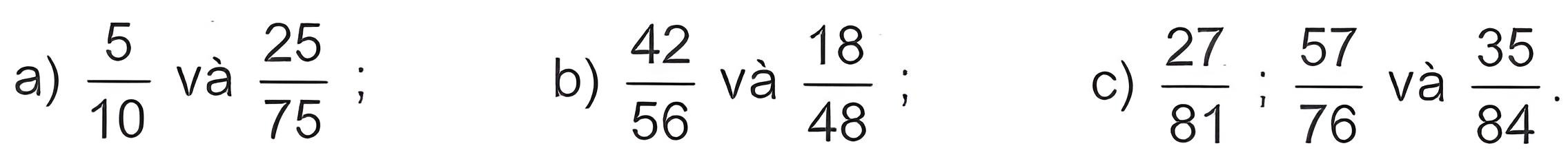
Lời giải:
2. Bài tập vận dụng
Bài 1: Quy đồng mẫu số các phân số:
a, và
b, và
Bài 2: Quy đồng mẫu số các phân số:
a, và
b, và
Bài 3: Quy đồng mẫu số các phân số:
a, và
b, và
c, và
d, và
Bài 4: Quy đồng mẫu số các phân số:
a,
b,
c,
d,
Bài 5: Hai phân số lần lượt bằng hai phân số và có mẫu chung bằng 42 là:
A,
B,
C,
Bài 6: Mẫu số chung bé nhất có thể có của 2 phân số và là số tự nhiên nào?
Bài 7: Ba phân số lần lượt bằng 3 phân số: là:
A,
B,
C,
Bài 8: Quy đồng mẫu số các phân số:
a,
b,
c,
d,
Bài 9: Hai phân số có mẫu của phân số thứ nhất là 12, mẫu của phân số thứ hai là 15. Sau khi quy đồng mẫu số (mẫu chung là số bé nhất chia hết cho 12 và 15) thì tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai là 9 đơn vị; tổng của hai tử số là 41. Tìm hai phân số ban đầu.
Bài 10: Viết các phân số và thành 2 phân số đều có mẫu số là 24.
Bài 11: Rút gọn rồi quy đồng các phân số:
và
Bài 12: Viết các phân số sau thành các phân số có mẫu số là 10: