Với tóm tắt lý thuyết Toán lớp 4 Quy đồng mẫu số các phân số hay, chi tiết cùng với 13 bài tập chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 4.

Lý thuyết Quy đồng mẫu số các phân số lớp 4 hay, chi tiết

A. Lý thuyết Quy đồng mẫu số các phân số

I. KIẾN THỨC CƠ BẢN

Lý thuyết:  

Khi quy đồng mẫu số hai phân số có thể làm như sau: 

Lấy tử số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

Ví dụ: Quy đồng mẫu số các phân số:  

Lời giải: 

Hai phân số 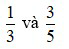  có mẫu số chung là 15.

Ta lấy tử số và mẫu số của phân số 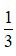 với 5, ta được:  .

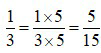Ta lấy tử số và mẫu số của phân số 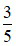 với 3 ta được:  .

Vậy quy đồng mẫu số hai phân số 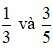  ta được hai phân số  .

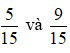II. CÁC DẠNG TOÁN

Dạng 1: Quy đồng mẫu số hai phân số

Phương pháp: 

Khi quy đồng mẫu số hai phân số có thể làm như sau: 

Lấy tử số của phân số thứ nhất nhân vớiS mẫu số của phân số thứ hai.

Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất,

Ví dụ: Quy đồng mẫu số hai phân số  .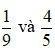

Lời giải: 

Hai phân số 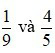   có mẫu số chung là 45.

Ta lấy tử số và mẫu số của phân số 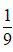 với 5, ta được:  .

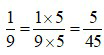Ta lấy tử số và mẫu số của phân số 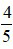 với 9 ta được:  .

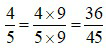Vậy quy đồng mẫu số hai phân số 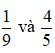 ta được hai phân số  .

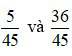Dạng 2: Quy đồng mẫu số hai phân số (Một mẫu chia hết cho mẫu còn lại)

Phương pháp: 

Nếu mẫu số của phân số thứ hai mà chia hết cho mẫu số của phân số thứ nhất thì ta có thể quy đồng mẫu số hai phân số như sau:

+ Lấy mẫu số chung là mẫu số của phân số thứ hai.

+ Tìm thừa số phụ bằng cách lấy mẫu số thứ hai cho cho mẫu số thứ nhất.

+ Nhân cả tử số và mẫu số của phân số thứ nhất với thừa số phụ tương ứng.

+ Giữ nguyên phân số thứ hai

Ví dụ: Quy đồng mẫu số hai phân số  .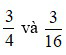

Lời giải:

Ta thấy mẫu số của phân số 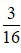 chia hết cho mẫu số của phân số  .

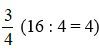Ta quy đồng mẫu số hai phân số 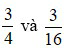  như sau:

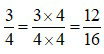 và giữ nguyên phân số  .

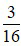Vậy quy đồng mẫu số hai phân số 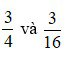  ta được hai phân số  .

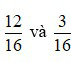B. Bài tập Biểu thức có chứa một chữ

I. TRẮC NGHIỆM 

Câu 1: Cho hai phân số $\frac{1}{2}$ và $\frac{1}{6}$. Mẫu số chung nhỏ nhất của hai phân số đó là gì?  

A. 6

B. 12

C. 18

D. 24

Câu 2: Mẫu số chung nhỏ nhất của hai phân số $\frac{5}{6}$ và $\frac{3}{24}$ là:

A.12

B. 24

C.18

D. 54

Câu 3: Quy đồng mẫu số hai phân số $\frac{3}{4}$ và $\frac{1}{5}$ (với mẫu số chung nhỏ nhất) ta được hai phân số mới tương ứng là: 

A. $\frac{15}{20}$và $\frac{1}{20}$

B. $\frac{3}{20}$và $\frac{1}{20}$

C. $\frac{15}{20}$và $\frac{4}{20}$

D. $\frac{15}{20}$ và $\frac{5}{20}$

Câu 4: Quy đồng mẫu số hai phân số $\frac{1}{17}$ và $\frac{5}{34}$ với mẫu số chung nhỏ nhất, ta được hai phân số mới lần lượt là:

A. $\frac{5}{17}$ và $\frac{1}{17}$.

B. $\frac{5}{34}$ và $\frac{17}{34}$.

C. $\frac{1}{34}$ và $\frac{5}{34}$

D. $\frac{2}{34}$ và $\frac{5}{34}$.

Câu 5: Quy đồng mẫu số hai phân số $\frac{7}{21}$ và $\frac{2}{3}$ ta được hai phân số mới là $\frac{7}{21}$ và …..

A. $\frac{3}{21}$

B. $\frac{2}{21}$

C. $\frac{14}{21}$

D. $\frac{9}{21}$

Câu 6: Hai phân số lần lượt bằng $\frac{5}{8}$ và $\frac{7}{12}$ có mẫu số chung bằng 24 là:

A. $\frac{20}{24}$ và $\frac{14}{24}$

B. $\frac{21}{24}$ và $\frac{18}{24}$

C. $\frac{15}{24}$ và $\frac{18}{24}$

D. $\frac{14}{24}$và $\frac{15}{24}$

Câu 7: Quy đồng mẫu số hai phân số $\frac{7}{12}$ và $\frac{5}{30}$ ta được:

A. $\frac{25}{60}$ và $\frac{10}{60}$

B. $\frac{7}{60}$ và $\frac{5}{60}$

C. $\frac{35}{60}$ và $\frac{10}{60}$

D. $\frac{21}{60}$ và $\frac{15}{60}$

Câu 8: Quy đồng mẫu số hai phân số $\frac{4}{19}$ và $\frac{1}{3}$ ta được:

A. $\frac{4}{57}$ và $\frac{3}{57}$.

B. $\frac{12}{19}$ và $\frac{1}{19}$.

C. $\frac{4}{19}$ và $\frac{3}{19}$.

D. $\frac{12}{57}$ và $\frac{19}{57}$.

II. TỰ LUẬN

Câu 1: Quy đồng mẫu số các phân số sau:  

a) $\frac{5}{4}$ và $\frac{11}{6}$

b) $\frac{3}{5}$ và $\frac{9}{7}$

c) $\frac{3}{7}$ và $\frac{1}{6}$

Câu 2:

a) Viết một phân số bằng phân số $\frac{5}{6}$ và có mẫu số là 30.

b) Viết một phân số bắng phân số $\frac{1}{2}$ và có mẫu số là 100.

Câu 3: Quy đồng mẫu số hai phân số $\frac{6}{27}$ và $\frac{4}{3}$ ta giữ nguyên phân số $\frac{6}{27}$, rồi nhân cả tử và mẫu của phân số $\frac{4}{3}$ với ……….

Câu 4: Quy đồng mẫu số các phân số:

a) $\frac{5}{9}$ và $\frac{3}{27}$

b) $\frac{7}{12}$ và $\frac{5}{6}$

c) $\frac{4}{11}$ và $\frac{5}{121}$

Câu 5: Điền số thích hợp vào chỗ chấm:  

a) $\frac{2}{47}=\frac{4}{\mathrm{.....}}=\frac{\mathrm{.....}}{141}$

b) Quy đồng mẫu số hai phân số $\frac{2}{3}$ và $\frac{7}{8}$ ta được hai phân số lần lượt là: $\frac{\mathrm{....}}{48}$ và $\frac{\mathrm{.....}}{\mathrm{.....}}$.