Với giải bài tập Toán lớp 6 Bài 3: Chu vi và diện tích của một số hình trong thực tiễn chi tiết bám sát nội dung sgk Toán 6 Tập 1 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:

Giải bài tập Toán 6 Bài 3: Chu vi và diện tích của một số hình trong thực tiễn 

Video giải Toán 6 Bài 3: Chu vi và diện tích của một số hình trong thực tiễn - Chân trời sáng tạo

A. Các câu hỏi trong bài

Giải Toán 6 trang 87 Tập 1 Chân trời sáng tạo

Hoạt động khởi động trang 87 Toán lớp 6 Tập 1: Để tính chu vi và diện tích một hình trong thực tiễn, thông thường ta chia hình đó thành các hình đã biết cách tính chu vi và diện tích.

Giải Toán 6 trang 88 Tập 1 Chân trời sáng tạo

Hoạt động khám phá 1 trang 88 Toán lớp 6 Tập 1: Quan sát Hình 1 rồi thực hiện các yêu cầu sau:

- Tính chu vi của hình bình hành ABCD.

- Diện tích tam giác AMD bằng diện tích tam giác nào?

- Diện tích hình bình hành ABCD bằng diện tích hình chữ nhật nào?

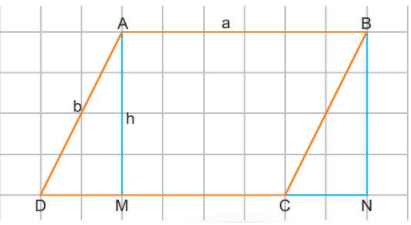
Lời giải:

- Chu vi của hình bình hành ABCD là tổng độ dài các cạnh AB, BC, CD, DA 

Ta có: AB + BC + CD + DA = a + b + a + b = 2(a + b)  (đvđd)

Do đó chu vi của hình bình hành ABCD là 2(a + b)          (đvđd)

- Quan sát trên hình vẽ, ta thấy diện tích tam giác AMD bằng diện tích tam giác BNC.

- Ta thấy điện tích hình bình hành ABCD bằng diện tích tam giác AMD cộng với diện tích hình ABCM.

Diện tích hình chữ nhật ABNM bằng diện tích tam giác BNC cộng với diện tích hình ABCM.

Mà diện tích tam giác AMD bằng diện tích tam giác BNC nên diện tích hình bình hành ABCD bằng diện tích hình chữ nhật ABNM.

Hoạt động khám phá 2 trang 88 Toán lớp 6 Tập 1: Quan sát Hình 2 rồi thực hiện các yêu cầu sau:

- Tính chu vi của hình thoi ABCD.

- So sánh diện tích hình thoi ABCD và diện tích hình chữ nhật AMNC.

- Tính diện tích hình chữ nhật AMNC theo m và n.

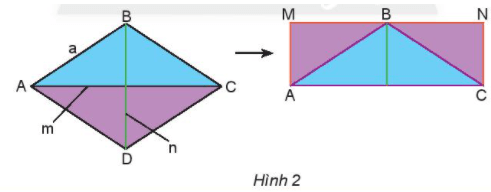
Lời giải:

- Chu vi hình thoi ABCD là tổng bốn cạnh của hình thoi, mà hình thoi có bốn cạnh bằng nhau và bằng a nên chu vi của hình thoi ABCD là:

a + a + a + a = 4a  (đvđd)

Do đó chu vi của hình thoi ABCD là 4a     (đvđd)

- Quan sát hình vẽ ta thấy: 

Diện tích hình thoi ABCD bằng diện tích hai tam giác xanh cộng với diện tích hai tam giác tím.

Diện tích hình chữ nhật AMNC cũng bằng diện tích hai tam giác xanh cộng với diện tích hai tam giác tím.

Do đó diện tích hình thoi ABCD bằng diện tích hình chữ nhật AMNC.

Chiều dài AC của hình chữ nhật bằng m, chiều rộng AM của hình chữ nhật bằng n : 2.

Khi đó, diện tích hình chữ nhật AMNC là: m.n:2 (đvdt).

Giải Toán 6 trang 89 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 89 Toán lớp 6 Tập 1: Trong bãi gửi xe người ta đang vẽ một mũi tên với các kích thước như hình bên hướng dẫn chiều xe chạy. Tính diện tích hình mũi tên.

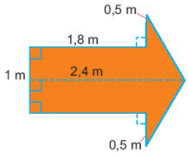
Gợi ý: Chia hình mũi tên thành các hình như bên dưới.

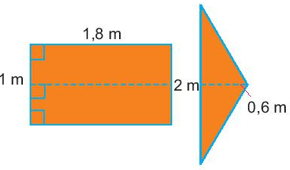
Lời giải:

Hình mũi tên được chia thành hai hình là hình chữ nhật và hình tam giác với kích thước như trên hình. 

Diện tích hình chữ nhật là: 1.1,8 = 1,8 (m²)

Diện tích hình tam giác là: (2.0,6):2 = 0.6 (m²)

Diện tích mũi tên là: 1,8 + 0,6 = 2,4 (m²)

Vậy diện tích mũi tên là 2,4 m²   

Giải Toán 6 trang 90 Tập 1 Chân trời sáng tạo

Vận dụng 1 trang 90 Toán lớp 6 Tập 1: Trong một khu vườn hình chữ nhật, người ta làm một lối đi lát sỏi với các kích thước như hình vẽ sau. Chi phí cho mỗi mét vuông làm lối đi hết 120 nghìn đồng. Hỏi chi phí để làm lối đi là bao nhiêu?

Lời giải:

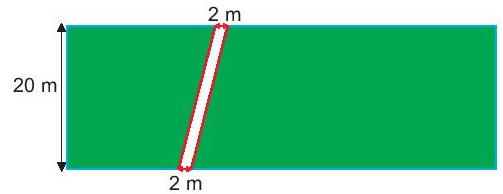
Lối đi trong khu vườn là hình bình hành nên diện tích của lối đi là: 2.20 = 40 (m²)

Chi phí để làm lối đi là: 40.120 000 = 4 800 000 (đồng).

Vậy chi phí để làm lối đi trong khu vườn hình chữ nhật là 4 800 000(đồng).

Thực hành 2 trang 90 Toán lớp 6 Tập 1: Người ta xây tường rào cho một khu vườn như hình bên. Mỗi mét dài (mét tới) tường rào tốn 150 nghìn đồng. Hỏi cần bao nhiêu tiền để xây tường rào?

Lời giải:

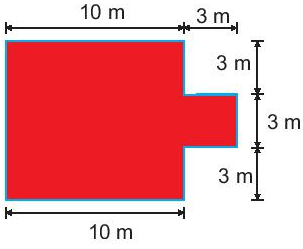
Vì người ta xây tường rào xung quanh khu vườn, nên số mét tường rào chính là chu vi của khu vườn. 

Chu vi của khu vườn đã cho là: 10.2 + 9 + 3 + 3 + 3 + 3 + 3= 44 (m)

Số tiền cần để làm tường rào là: 44.150 000 = 6 600 000(đồng)

Vậy cần 6 600 000 đồng để xây tường rào.

Vận dụng 2 trang 90 Toán lớp 6 Tập 1: Thầy giáo ra bài toán: Tính chu vi và diện tích một khu vườn hình chữ nhật có chiều rộng 25 m, chiều dài 300 dm.

Bạn An thực hiện như sau:

(25 + 300).2 = 650

Chu vi khu vườn 650 m.

25.300 = 7 500

Diện tích khu vườn 7500 m².

Thầy giáo bảo bạn An đã làm sai. Em hãy chỉ ra bạn An sai chỗ nào. Hãy sửa lại cho đúng.

Lời giải:

Bạn An sai ở chỗ chưa đổi chiều dài về cùng đơn vị với chiều rộng.

Sửa lại như sau:

Đổi 300 dm = 30 m.

Chu vi khu vườn hình chữ nhật là:

(25 + 30).2 = 110 (m).

Diện tích khu vườn hình chữ nhật là: 

 25.30 = 750 (m²)

Vậy diện tích khu vườn 750 m².

Chu vi khu vườn 110 m.

Nhận xét: Qua bài tập này, chúng ta cần chú ý khi tính chu vi và diện tích thì các kích thước phải cùng đơn vị đo.

B. Bài tập

Bài 1 trang 90 Toán lớp 6 Tập 1: Tính diện tích các hình sau:

a) Hình bình hành có chiều dài một cạnh 20 cm và chiều cao tương ứng 5 cm.

b) Hình thoi có độ dài hai đường chéo là 5 m và 20 dm.

c) Hình thang cân có độ dài hai cạnh đáy là 5 m và 3,2 m; chiều cao là 4 m.

Lời giải:

a) Diện tích hình bình hành là: 20.5 = 100 (cm²)

Vậy diện tích hình bình hành là 100 cm²

b) Đổi 20 dm = 2 m.

Diện tích hình thoi là: (5.2):2 = 5 (m²)

Vậy diện tích hình thoi là 5m².

c) Diện tích hình thang cân là: (5 + 3,2).4:2 = 16,4 (m²).

Vậy diện tích hình thang cân là 16,4 m²

Giải Toán 6 trang 91 Tập 1 Chân trời sáng tạo

Bài 2 trang 91 Toán lớp 6 Tập 1: Tính diện tích và chu vi các hình được tô màu sau:

a) 

b)

Lời giải:

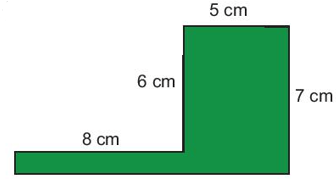
a) 

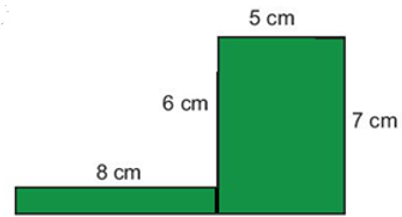
Chu vi của hình đã cho là: 8 + 6 + 5 + 7 + (8 + 5) +1 = 40 (cm).

Chia hình ban đầu thành hai hình như hình vẽ. Khi đó ta có:

Diện tích hình chữ nhật to là: 5.7 = 35 (cm² )

Diện tích hình chữ nhật nhỏ là: 8.(7 – 6) = 8 (cm² )

Diện tích hình ban đầu là: 35 + 8 = 43 (cm²)

Vậy diện tích hình được tô màu là  43 cm² và chu vi hình được tô màu là 40 cm.

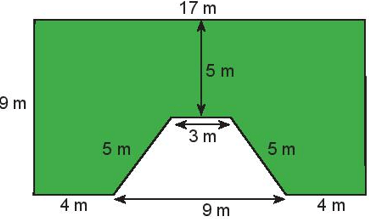
b)

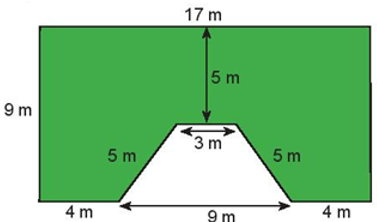
Chu vi hình được tô màu là: 9 + 4 + 5 + 3 + 5 + 4 + 9 + 17 = 56 (m).

Diện tích hình chữ nhật có hai kích thước là 9 m và 17 m là: 9.17 = 153 (m²)

Diện tích hình thang cân màu trắng trên hình là: (9 + 3). (9 – 5) : 2 = 24 ( m²)

Diện tích phần được tô màu bằng diện tích hình chữ nhật trừ đi diện tích hình thang cân màu trắng. Khi đó diện tích phần tô màu là: 153 – 24 = 129(m² )

Vậy chu vi hình được tô màu là 56m, diện tích phần tô màu là 129 m².

Bài 3 trang 91 Toán lớp 6 Tập 1: Một mảnh vườn có hình dạng như hình vẽ bên. Để tính diện tích mảnh vườn, người ta chia nó thành hình thang cân ABCD và hình bình hành ADEF có kích thước như sau: BC = 30 m; AD = 42 m, BM = 22 m, EN = 28 m. Hãy tính diện tích mảnh vườn này.

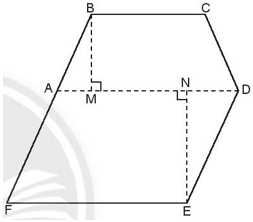
Lời giải:

Diện tích hình thang cân ABCD là: (30 + 42).22 : 2 = 792 ( m²)

Diện tích hình bình hành ADEF là: 42.28 = 1176 (m²)

Diện tích mảnh vườn là:792 + 1176 = 1968 (m²)

Vậy diện tích mảnh vườn là 1968 m²

Bài 4 trang 91 Toán lớp 6 Tập 1: Một khu vườn hình chữ nhật có chiều dài 25 m, chiều rộng 15 m. Ở giữa khu vườn người ta xây một bồn hoa hình thoi có độ dài hai đường chéo là 5 m và 3 m. Tính diện tích phần còn lại của khu vườn.

Lời giải:

Diện tích khu vườn hình chữ nhật là: 25.15 = 375 (m²).

Diện tích bồn hoa hình thoi là: 5.3:2 = 7,5 (m²).

Diện tích phần còn lại của mảnh vườn là: 375 – 7,5 = 367,5 (m²).

Vậy diện tích phần còn lại là 367,5 m².

Lý thuyết Chu vi và diện tích của một số hình trong thực tiễn

1. Chu vi và diện tích hình chữ nhật

Cho hình chữ nhật có chiều dài là a, chiều rộng là b (như hình vẽ).

Chu vi của hình chữ nhật là: P = (a + b) . 2

Diện tích của hình chữ nhật là: S = a . b

Ví dụ: Cho hình chữ nhật EFGH có EF = GH = 6 cm; EH = FG = 3 cm. Tính chu vi và diện tích hình chữ nhật EFGH.

Hướng dẫn giải

Chu vi hình chữ nhật EFGH là:

(6 + 3) . 2 = 18 (cm)

Diện tích hình chữ nhật EFGH là:

6 . 3 = 18 (cm²).

Vậy hình chữ nhật EFGH có chu vi là 18 cm và diện tích là 18 cm².

2. Chu vi và diện tích của hình vuông

Cho hình vuông có độ dài một cạnh bằng a (như hình vẽ).

Chu vi hình vuông là: P = 4a.

Diện tích hình vuông là: S = a . a = a².

Ví dụ: Một mảnh ruộng hình vuông có cạnh bằng 15m. Năng suất lúa là 0,9 kg/m². Tính sản lượng thu hoạch được trên mảnh ruộng hình vuông.

Hướng dẫn giải

Diện tích mảnh ruộng hình vuông là:

15² = 225 (m²).

Sản lượng thu hoạch được là:

225 : 0,9 = 312,5 (kg).

Vậy sản lượng thu hoạch được trên mảnh ruộng hình vuông là 312,5 kg.

3. Chu vi và diện tích của hình tam giác

Cho tam giác có độ dài ba cạnh lần lượt là a, b, c và chiều cao tương ứng với cạnh a có độ dài là h (như hình vẽ).

Chu vi hình hình tam giác là: P = a + b + c.

Diện tích hình tam giác là: 

Ví dụ: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm, BC = 5 cm. Tính chu vi và diện tích tam giác ABC.

Hướng dẫn giải

Chu vi tam giác ABC là:

3 + 4 + 5 = 12 (cm).

Diện tích tam giác ABC là:

Vậy tam giác ABC có chu vi là 12 cm và diện tích là 6 cm².

4. Chu vi và diện tích của hình thang

Cho hình thang có độ dài bốn cạnh là a, b, c, d và đường cao h (như hình vẽ).

Chu vi của hình thang là: P = a + b + c + d

Diện tích của hình thang là:

Ví dụ: Tính diện tích hình thang cân có độ dài hai đáy là 5 m và 3,5 m; chiều cao là 4 m.

Hướng dẫn giải

Diện tích hình thang cân là:

Vậy diện tích hình thang cân là 17 cm².

5. Chu vi và diện tích hình bình hành

Cho hình bình hành có độ dài hai cạnh là a và b, chiều cao tương ứng với một cạnh a có độ dài là h (như hình vẽ).

Chu vi hình bình hành là: P = 2(a + b).

Diện tích hình bình hành là: S = a . h.

Ví dụ: Hình bình hành có độ dài một cạnh là 12 cm và chiều cao tương ứng là 8 cm.

Khi đó, diện tích của hình bình hành là:

12 . 8 = 96 (cm²).

6. Chu vi và diện tích hình thoi

Cho hình thoi có độ dài một cạnh là a, độ dài hai đường chéo của hình thoi là m và n.

Chu vi của hình thoi là: P = 4a.

Diện tích của hình thoi là: 

Ví dụ: Hình thoi có độ dài hai đường chéo là 60 m và 50 m có diện tích là:

6. Chu vi và diện tích của một số hình trong thực tiễn

a) Tính chu vi của một số hình trong thực tiễn:

Chu vi của một hình bằng tổng độ dài các đoạn thẳng bao quanh hình đó.

b) Tính diện tích của một số hình trong thực tiễn:

− Nếu hình đã cho là các hình đã biết công thức như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, … thì ta áp dụng công thức và tính.

− Nếu hình đã cho không phải các hình đã biết công thức tính thì ta chia hình đã cho thành các hình đã biết công thức tính như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, …

Ví dụ: Tính chu vi và diện tích hình được tô màu sau:

Hướng dẫn giải

Chu vi của hình đã cho là:

8 + 6 + 5 + 7 + (8 + 5) +1 = 40 (cm).

Chia hình ban đầu thành hai hình như hình vẽ. Khi đó ta có:

Diện tích hình chữ nhật to là: 

5 . 7 = 35 (cm²).

Diện tích hình chữ nhật nhỏ là: 

8 . (7 – 6) = 8 (cm²).

Diện tích hình ban đầu là: 

35 + 8 = 43 (cm²).

Vậy hình được tô màu có chu vi là 40 cm và diện tích là 43 cm².

Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Hình chữ nhật - Hình thoi - Hình bình hành - Hình thang cân

Bài 4: Hoạt động thực hành và trải nghiệm: Tính chu vi và diện tích của một số hình trong thực tiễn

Bài tập cuối chương 3

Bài 1: Thu thập và phân loại dữ liệu