Với giải sách bài tập Toán 6 Bài 3: Chu vi và diện tích một số hình trong thực tiễn sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 3: Chu vi và diện tích một số hình trong thực tiễn

Bài 1 trang 75 sách bài tập Toán lớp 6 Tập 1: Tính chu vi và diện tích của hình bên, biết AB = AD = 4 cm, BC = CD = 2 cm, các góc B và D đều là góc vuông

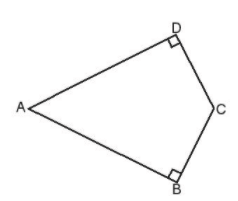
Lời giải:

Chu vi của hình là:

AB + BC + CD + DA = 4 + 2 + 2 + 4 = 12 (cm)

Ta chia hình trên thành hai tam giác, như sau:

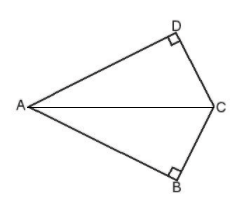
Diện tích của hình ABCD bằng diện tích tam giác ABC cộng với diện tích tam giác ADC và bằng: 

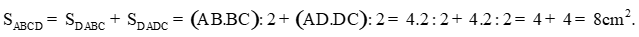
Vậy chu vi của hình trên là 12cm và diện tích của hình trên là 8 cm².

Bài 2 trang 75 sách bài tập Toán lớp 6 Tập 1: Tính chu vi và diện tích của hình bên, biết AB = 7 cm, BC = 2 cm, CD = 3 cm và DE = 3 cm

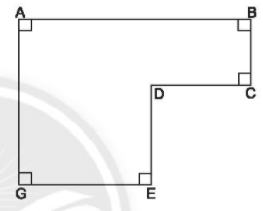
Lời giải:

Dựa vào hình vẽ, ta có:

GE = AB - CD = 7 - 3 = 4 (cm)

AG = BC + DE = 2 + 3 = 5 (cm)

Chu vi của hình là:

P = AB + BC + CD + DE + EG + GA = 7 + 2 + 3 + 3 + 4 + 5 = 24 (cm)

Phân chia thành 2 hình chữ nhật 

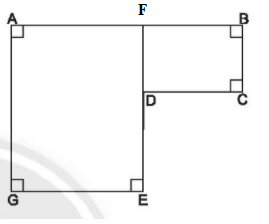
Diện tích hình chữ nhật AFEG có chiều rộng là GE = 4cm, AG = 5cm là: 

4.5 = 20 (cm²).

Diện tích hình chữ nhật FBCD có chiều rộng là BC = 2cm, CD = 3cm là: 

2.3 = 6 (cm²).

Khi đó ta có diện tích của hình đã cho bằng diện tích hình chữ nhật AFEG cộng với diện tích hình chữ nhật FBCD bằng:

S = 20 + 6 = 26 (cm²).

Bài 3 trang 75 sách bài tập Toán lớp 6 Tập 1: Tính chu vi của hình bên, biết BCDE là hình chữ nhật có diện tích 135m², BC = 15 m, ABGK là hình chữ nhật có diện tích 180 m², BE = EG.

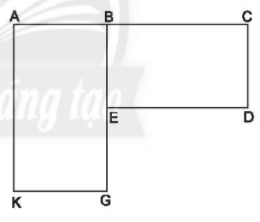
Lời giải:

Vì diện tích hình chữ nhật BCDE bằng BE.BC = 135 nên BE = 135 : 15 = 9 (m)

Suy ra EG = BE = 9 m 

Mà BG = EG + BE = 9 + 9 = 18 m.

Suy ra AK = BG = 18 m

Vì diện tích hình chữ nhật AB.BG = 180 nên AB = 180 : 18 = 10 (m)

Suy ra KG = AB = 10 m.

Suy ra AC = AB + BC = 10 + 15 = 25 (m).

Chu vi của hình cần tìm là:

AC + CD + DE + EG + GK + AK = 25 + 9 + 15 + 9 + 10 + 18

   = 86 (m).

Vậy chu vi của hình cần tìm là 86 m.

Bài 4 trang 75 sách bài tập Toán lớp 6 Tập 1: Một mảnh vườn hình chữ nhật có chiều dài 40 m, chiều rộng 30 m với lối đi hình bình hành rộng 2 m (xem hình dưới). Tính diện tích phần mảnh vườn không tính lối đi.

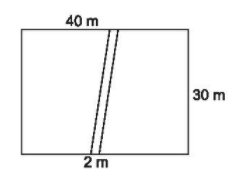
Lời giải:

Diện tích của cả mảnh vườn là:

40.30 = 1 200 (m²)

Diện tích lối đi là: 

2.30 = 60 (m²)

Diện tích phần mảnh vườn không tính lối đi là:

1 200 - 60 = 1 140 (m²)

Vậy diện tích phần mảnh vườn không tính lối đi là: 1 140 m².

Bài 5 trang 76 sách bài tập Toán lớp 6 Tập 1: Khu đậu xe ô tô của một cửa hàng có dạng hình chữ nhật với chiều dài 14 m, chiều rộng 10 m. Trong đó, một nửa khu vực dành cho quay đầu xe, hai góc tam giác để trồng hoa và phần còn lại chia đều cho bốn chỗ đậu xe ô tô (xem hình)

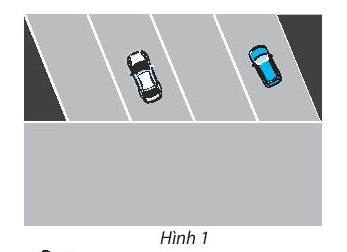
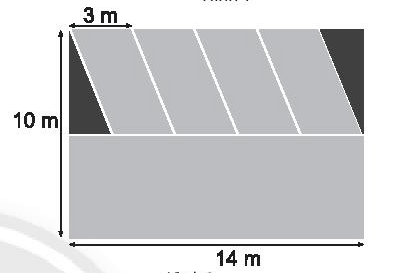
a) Tính diện tích chỗ đậu xe dành cho một ô tô.

b) Tính diện tích dành cho đậu xe và quay đầu xe.

Lời giải:

a) Chỗ đậu xe là hình bình hành có chiều cao là: 10:2 = 5 (m).

Diện tích mỗi chỗ đậu xe là: 3.5 = 15 (m²).

Vậy diện tích chỗ đậu xe dành cho một ô tô là: 15m².

b) Diện tích hình chữ nhật là: 10.14 = 140 (m²)

Cạnh còn lại của một góc tam giác là: 14 – 3.4 = 14 – 12 = 2 (m).

Diện tích một góc tam giác là: 2.5:2 = 5 (m²)

Diện tích phần trồng hoa bằng diện tích hai góc tam giác và bằng: 2.5 = 10 (m²)

Diện tích dành cho quay đầu xe và đậu xe: 140 - 10 = 130 (m²).

Vậy diện tích dành cho việc đậu xe và quay đầu xe là 130 m²_.

Bài 6 trang 76 sách bài tập Toán lớp 6 Tập 1: Tính diện tích của hình bên biết AB = 6cm, OB = 3cm, OG = 4cm, CD = 12cm, ABCD là hình thang, BCEG là hình thoi, ba điểm A, B, E thẳng hàng.

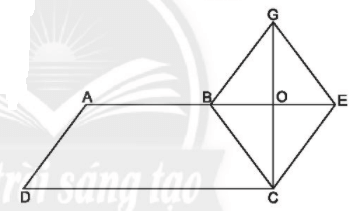
Lời giải:

Ta có: BE = 2.OB = 6 cm; CG = 2.OG = 8 cm

Diện tích hình thoi BCEG là: BE.CG:2 = 8.6:2 = 24 (cm²)

Diện tích hình thang ABCD là: (AB + CD).OC:2 = (6 + 12).4:2 = 36 (cm²)

Diện tích hình cần tìm bằng diện tích hình thang ABCD cộng với diện tích hình thoi BCEG bằng:  24 + 36 = 60 (cm²).

Vậy diện tích hình cần tìm là 60 cm².

Lý thuyết Chu vi và diện tích của một số hình trong thực tiễn

1. Chu vi và diện tích hình chữ nhật

Cho hình chữ nhật có chiều dài là a, chiều rộng là b (như hình vẽ).

Chu vi của hình chữ nhật là: P = (a + b) . 2

Diện tích của hình chữ nhật là: S = a . b

Ví dụ: Cho hình chữ nhật EFGH có EF = GH = 6 cm; EH = FG = 3 cm. Tính chu vi và diện tích hình chữ nhật EFGH.

Hướng dẫn giải

Chu vi hình chữ nhật EFGH là:

(6 + 3) . 2 = 18 (cm)

Diện tích hình chữ nhật EFGH là:

6 . 3 = 18 (cm²).

Vậy hình chữ nhật EFGH có chu vi là 18 cm và diện tích là 18 cm².

2. Chu vi và diện tích của hình vuông

Cho hình vuông có độ dài một cạnh bằng a (như hình vẽ).

Chu vi hình vuông là: P = 4a.

Diện tích hình vuông là: S = a . a = a².

Ví dụ: Một mảnh ruộng hình vuông có cạnh bằng 15m. Năng suất lúa là 0,9 kg/m². Tính sản lượng thu hoạch được trên mảnh ruộng hình vuông.

Hướng dẫn giải

Diện tích mảnh ruộng hình vuông là:

15² = 225 (m²).

Sản lượng thu hoạch được là:

225 : 0,9 = 312,5 (kg).

Vậy sản lượng thu hoạch được trên mảnh ruộng hình vuông là 312,5 kg.

3. Chu vi và diện tích của hình tam giác

Cho tam giác có độ dài ba cạnh lần lượt là a, b, c và chiều cao tương ứng với cạnh a có độ dài là h (như hình vẽ).

Chu vi hình hình tam giác là: P = a + b + c.

Diện tích hình tam giác là: 

Ví dụ: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm, BC = 5 cm. Tính chu vi và diện tích tam giác ABC.

Hướng dẫn giải

Chu vi tam giác ABC là:

3 + 4 + 5 = 12 (cm).

Diện tích tam giác ABC là:

Vậy tam giác ABC có chu vi là 12 cm và diện tích là 6 cm².

4. Chu vi và diện tích của hình thang

Cho hình thang có độ dài bốn cạnh là a, b, c, d và đường cao h (như hình vẽ).

Chu vi của hình thang là: P = a + b + c + d

Diện tích của hình thang là:

Ví dụ: Tính diện tích hình thang cân có độ dài hai đáy là 5 m và 3,5 m; chiều cao là 4 m.

Hướng dẫn giải

Diện tích hình thang cân là:

Vậy diện tích hình thang cân là 17 cm².

5. Chu vi và diện tích hình bình hành

Cho hình bình hành có độ dài hai cạnh là a và b, chiều cao tương ứng với một cạnh a có độ dài là h (như hình vẽ).

Chu vi hình bình hành là: P = 2(a + b).

Diện tích hình bình hành là: S = a . h.

Ví dụ: Hình bình hành có độ dài một cạnh là 12 cm và chiều cao tương ứng là 8 cm.

Khi đó, diện tích của hình bình hành là:

12 . 8 = 96 (cm²).

6. Chu vi và diện tích hình thoi

Cho hình thoi có độ dài một cạnh là a, độ dài hai đường chéo của hình thoi là m và n.

Chu vi của hình thoi là: P = 4a.

Diện tích của hình thoi là: 

Ví dụ: Hình thoi có độ dài hai đường chéo là 60 m và 50 m có diện tích là:

6. Chu vi và diện tích của một số hình trong thực tiễn

a) Tính chu vi của một số hình trong thực tiễn:

Chu vi của một hình bằng tổng độ dài các đoạn thẳng bao quanh hình đó.

b) Tính diện tích của một số hình trong thực tiễn:

− Nếu hình đã cho là các hình đã biết công thức như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, … thì ta áp dụng công thức và tính.

− Nếu hình đã cho không phải các hình đã biết công thức tính thì ta chia hình đã cho thành các hình đã biết công thức tính như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, …

Ví dụ: Tính chu vi và diện tích hình được tô màu sau:

Hướng dẫn giải

Chu vi của hình đã cho là:

8 + 6 + 5 + 7 + (8 + 5) +1 = 40 (cm).

Chia hình ban đầu thành hai hình như hình vẽ. Khi đó ta có:

Diện tích hình chữ nhật to là: 

5 . 7 = 35 (cm²).

Diện tích hình chữ nhật nhỏ là: 

8 . (7 – 6) = 8 (cm²).

Diện tích hình ban đầu là: 

35 + 8 = 43 (cm²).

Vậy hình được tô màu có chu vi là 40 cm và diện tích là 43 cm².