Với tóm tắt lý thuyết Toán lớp 6 Bài 6: Chia hết và chia có dư, Tính chất chia hết của một tổng sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 6: Chia hết và chia có dư, Tính chất chia hết của một tổng

Video giải Toán 6 Bài 6: Chia hết và chia có dư, Tính chất chia hết của một tổng - Chân trời sáng tạo

A. Lý thuyết Chia hết và chia có dư, Tính chất chia hết của một tổng

1. Chia hết và chia có dư

Cho hai số tự nhiên a và b, trong đó b khác 0. Ta luôn tìm được đúng hai số tự nhiên q và r sao cho a = b . q + r, trong đó 0 ≤ r < b. Ta gọi q và r lần lượt là thương và số dư trong phép chia a cho b.

− Nếu r = 0 tức a = b . q, ta nói a chia hết cho b, kí hiệu a ⋮ b và ta có phép chia hết a : b = q . a

− Nếu r ≠ 0, ta nói a không hết cho b, kí hiệu a ⋮̸ b và ta có phép chia có dư.

Ví dụ: Hãy tìm số dư trong phép chia mỗi số sau đây cho 3: 279; 517; 8 126.

Hướng dẫn giải

a) Ta có: 279 = 93 . 3 + 0

Do đó 279 chia hết cho 3.

Ta có: 517 = 172 . 3 + 1

Do đó 517 chia cho 3 dư 1.

Ta có: 8 126 = 2 708 . 3 + 2

Do đó 8 126 chia cho 3 dư 2.

Vậy 279 chia hết cho 3; 517 chia cho 3 dư 1; 8 126 chia cho 3 dư 2.

2. Tính chất chia hết của một tổng

Tính chất 1

Cho a, b, n là các số tự nhiên, n khác 0.

Nếu a ⋮ n và b ⋮ n thì (a + b) ⋮ n và (a − b) ⋮ n (a ≥ b)

Nếu a ⋮ n, b ⋮ n và c ⋮ n thì (a + b + c) ⋮ n.

Ví dụ: Tổng sau có chia hết cho 8 không?

132 . 8 + 24 . 2022.

Hướng dẫn giải

Vì 8 ⋮ 8 nên 132 . 8 ⋮ 8;

Vì 24 ⋮ 8 nên 24 . 2022 ⋮ 8.

Ta có 132 . 8 ⋮ 8 và 24 . 2022 ⋮ 8.

Do đó (132 . 8 + 24 . 2022) ⋮ 8.

Vậy tổng đã cho chia hết cho 8.

Tính chất 2

Cho a, b, n là các số tự nhiên, n khác 0 (a ≥ b).

Nếu a ⋮̸ n và b ⋮ n thì (a + b) ⋮̸ n và (a − b) ⋮̸ n.

Nếu a ⋮ n và b ⋮̸ n thì (a + b) ⋮̸ n và (a − b) ⋮̸ n.

Nếu a ⋮̸ n, b ⋮ n và c ⋮ n thì (a + b + c) ⋮̸ n.

Nếu trong một tổng chỉ có đúng một số hạng không chia hết cho một số, các số hạng còn lại đều chia hết cho số đó thì tổng không chia hết cho số đó.

Ví dụ: Tổng sau có chia hết cho 12 không?

36 . 75 + 15.

Hướng dẫn giải

Vì 36 ⋮ 12 nên 36 . 75 ⋮ 12

Ta có 36 . 75 ⋮ 12 và 15 ⋮̸ 12.

Do đó (36 . 75 + 15) ⋮̸ 12.

Vậy tổng đã cho không chia hết cho 12.

B. Bài tập tự luyện

Bài 1. Không tính tổng, hãy kiểm tra:

a) 6 + 9 + 15 có chia hết cho 3 không?

b) 75 + 12 có chia hết cho 15 không?

c) 10 + 15 + 12 có chia hết cho 3 không?

Hướng dẫn giải

a) Vì 6 ⋮ 3; 9 ⋮ 3; 15 ⋮ 3 nên (6 + 9 + 15) ⋮ 3.

Vậy 6 + 9 + 15 chia hết cho 3.

b) Vì 75 ⋮ 15 và 12 ⋮̸ 15 nên (75 + 12) ⋮̸ 15.

Vậy 75 + 12 không chia hết cho 15.

c) Vì 10 ⋮ 5; 15 ⋮ 5; 12 ⋮̸ 5 nên (10 + 15 + 12) ⋮̸ 5

Vậy 10 + 15 + 12 không chia hết cho 5.

Bài 2. Cho tổng M = 105 + 72 + x. Để M chia hết cho 3 thì x phải như thế nào?

Hướng dẫn giải

Vì 105 ⋮ 3; 72 ⋮ 3 nên để M = 105 + 72 + x chia hết cho 3 thì x ⋮ 3.

Vậy để M chia hết cho 3 thì x phải chia hết cho 3.

Bài 3. Tìm d để 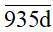 vừa chia hết cho 3 vừa chia hết cho 2.

Hướng dẫn giải

Điều kiện để d vừa chia hết cho 2 vừa chia hết cho 3 thì:

d là số chẵn và (9 + 3 + 5 + d) ⋮ 3.

Ta có: (9 + 3 + 5 + d) = 17 + d.

Để (17 + d) ⋮ 3 thì d = 1 hoặc d = 4.

Mà d là số chẵn nên d = 4.

Vậy để 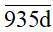 vừa chia hết cho 3 vừa chia hết cho 2 thì d = 4.

Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 5: Thứ tự thực hiện các phép tính

Lý thuyết Bài 6: Chia hết và chia có dư, Tính chất chia hết của một tổng

Lý thuyết Bài 7: Dấu hiệu chia hết cho 2, cho 5

Lý thuyết Bài 8: Dấu hiệu chia hết cho 3, cho 9

Lý thuyết Bài 9: Ước và bội